[数据结构与算法] 背包问题九讲（自用）+货币系统（方案数）

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 背包问题九讲（自用）+货币系统（方案数） -> 正文阅读

[数据结构与算法]背包问题九讲（自用）+货币系统（方案数）

1. 01背包问题
2. 完全背包问题
3. 多重背包问题
4. 混合背包问题
5. 二维费用背包问题
6. 分组背包问题
7. 背包问题求方案数
8. 求背包问题的方案
9. 有依赖的背包问题

01背包问题

二维数组

#include <bits/stdc++.h>

using namespace std;

int n,m;
int dp[1005][1005]={0};
int v,w;

int main(){
    
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> v >> w;
        for(int j=0;j<=m;j++){
            if(j<v){//取不到
                dp[i][j]=dp[i-1][j];
            }else{//能取：1.想取 2.不想取
                dp[i][j]=max(dp[i-1][j],dp[i-1][j-v]+w);
            }
        }
    }
    cout << dp[n][m] << endl;
    return 0;
}

滚动数组(优化)
思路：第二层循环需要从大到小循环，因为用到原值，而不是新值。

#include <bits/stdc++.h>

using namespace std;

int n,m;
int dp[1005]={0};
int v,w;

int main(){
    
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> v >> w;
        for(int j=m;j>=v;j--){//能取：1.想取 2.不想取
            dp[j]=max(dp[j],dp[j-v]+w);
        }
    }
    cout << dp[m] << endl;
    return 0;
}

完全背包问题

二维数组（三重循环）（朴素写法）

#include <bits/stdc++.h>

using namespace std;

int n,m;
int dp[1005][1005]={0};
int v,w;

int main(){
    
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> v >> w;
        for(int j=0;j<=m;j++){
            for(int k=0;k*v<=j;k++){//能取：取任意个[0,]
                dp[i][j]=max(dp[i][j],dp[i-1][j-k*v]+k*w);
            }
        }
    }
    cout << dp[n][m] << endl;
    return 0;
}

二重循环（优化）

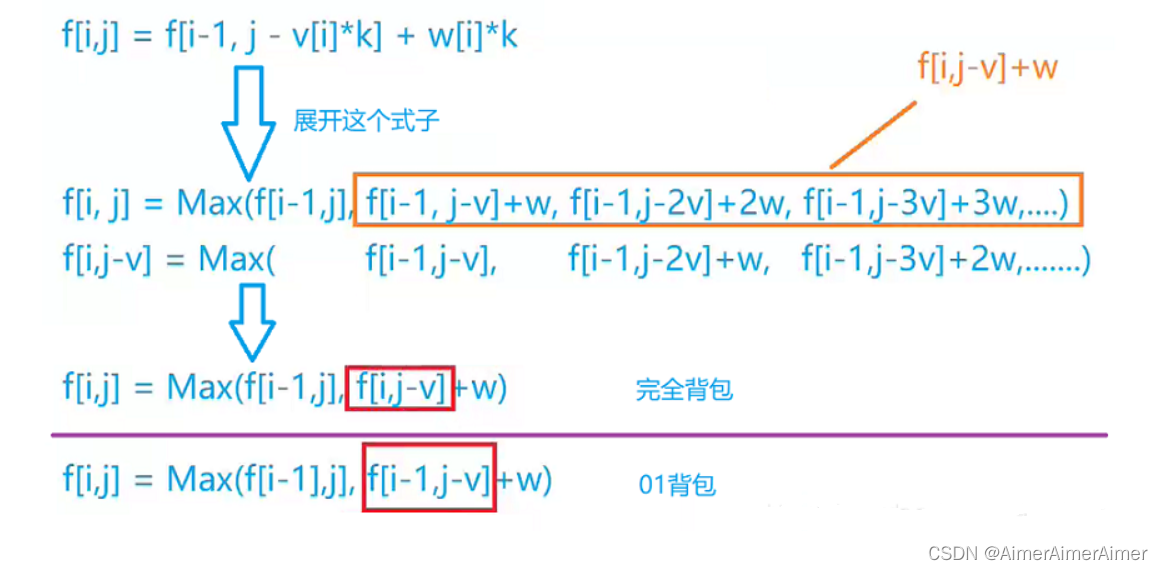
思路：公式化简，消除第三层循环
在这里插入图片描述
讲解的图

#include <bits/stdc++.h>

using namespace std;

int n,m;
int dp[1005][1005]={0};
int v,w;

int main(){
    
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> v >> w;
        for(int j=0;j<=m;j++){
            if(j<v){//取不到
                dp[i][j]=dp[i-1][j];
            }else{//能取: 1.不想取 2.想取
                dp[i][j]=max(dp[i-1][j],dp[i][j-v]+w);
            }
        }
    }
    cout << dp[n][m] << endl;
    return 0;
}

滚动数组（再优化）

思路：因为不需要用到上一行数据，要用到本行之前计算出来的数据，因此第二层循环应该从小到大进行遍历

#include <bits/stdc++.h>

using namespace std;

int n,m;
int dp[1005]={0};
int v,w;

int main(){
    
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> v >> w;
        for(int j=v;j<=m;j++){//能取: 1.不想取 2.想取
            
            dp[j]=max(dp[j],dp[j-v]+w);
        }
    }
    cout << dp[m] << endl;
    return 0;
}

多重背包问题

朴素写法（三重循环）

#include <bits/stdc++.h>

using namespace std;

int n,m;
int dp[105][105]={0};
int v,w,s;

int main(){
    
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> v >> w >> s;
        for(int j=0;j<=m;j++){
            for(int k=0;k<=s&&k*v<=j;k++){//能取：取[0,s]个
            //包含想取和不想取
                dp[i][j]=max(dp[i][j],dp[i-1][j-k*v]+k*w);
            }
        }
    }
    cout << dp[n][m] << endl;
    return 0;
}

不能像完全背包一样化简公式的原因：当 j (体积)很大时，j-v还是很大，所以k*v依然<=j-v,因此公式会多一项
在这里插入图片描述

（二进制优化+滚动数组）

例如 s=10
10可以拆分为0、1、2、4、3；
前四个数可以凑出0~7之间的任何数据，加上3可以凑出3~10之间的任何数据，因此这5个数可以凑出0~10内的任何数据；
相当于将10个物品打包成4个物品，打包后的物品的体积和价值分别为单个物品的1、2、4、3倍；
这四个物品都是可选可不选，因此就转化成了01背包问题。

#include <bits/stdc++.h>

using namespace std;

int n,m,v,w,s;
vector<pair<int,int>> goods;//存储二进制组合商品的体积和价值
int dp[2005];

int main(){
    
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> v >> w  >> s;
        for(int j=1;j<=s;j*=2){//每种商品都二进制拆解
            goods.push_back({j*v,j*w});
            s-=j;
        }
        if(s>0){
            goods.push_back({s*v,s*w});
        }
    }
    
    int len=goods.size();
    for(int i=1;i<=len;i++){
        
        v=goods[i-1].first;
        w=goods[i-1].second;
        
        for(int j=m;j>=v;j--){//能取：1.不想取 2.想取
            dp[j]=max(dp[j],dp[j-v]+w);
        }
    }
    cout << dp[m] << endl;
    
    return 0;
}

（单调队列优化，待续。。。）

混合背包问题

#include <bits/stdc++.h>

using namespace std;

int n,m,v,w,s;
int dp[1005];

int main(){
    
    cin >> n >> m;
    for(int i=0;i<n;i++){
        cin >> v >> w >> s;
        if(s==-1){//01背包
            
            for(int j=m;j>=v;j--){
                dp[j]=max(dp[j],dp[j-v]+w);
            }
            
        }else if(s==0){//完全背包
            
            for(int j=v;j<=m;j++){
                dp[j]=max(dp[j],dp[j-v]+w);
            }
            
        }else{//多重背包
            //二进制优化
            for(int t=1;t<=s;t*=2){//二进制拆解,转换成01背包
            
                for(int j=m;j>=t*v;j--){
                    dp[j]=max(dp[j],dp[j-t*v]+t*w);
                }
                
                s-=t;
            }
            if(s>0){
                for(int j=m;j>=s*v;j--){
                    dp[j]=max(dp[j],dp[j-s*v]+s*w);
                }
            }
        }
    }
    cout << dp[m] << endl;
    return 0;
}

二维费用背包问题（每件物品只能用一次）

思路：二个参数限制。

三维数组

#include <bits/stdc++.h>

using namespace std;

int n,V,M,v,m,w;
int dp[1005][105][105];

int main(){
    
    cin >> n >> V >> M;
    for(int i=1;i<=n;i++){//两个参数限制
        cin >> v >> m >> w;
        for(int j=0;j<=V;j++){
            for(int k=0;k<=M;k++){
                if(j>=v&&k>=m){//能取: 1.不想取 2.想取
                    dp[i][j][k]=max(dp[i-1][j][k],dp[i-1][j-v][k-m]+w);
                }else{//不能取
                    dp[i][j][k]=dp[i-1][j][k];
                }
            }
        }
        
    }
    cout << dp[n][V][M] << endl;
    return 0;
}

二维数组（优化）

#include <bits/stdc++.h>

using namespace std;

int n,V,M,v,m,w;
int dp[105][105];

int main(){
    
    cin >> n >> V >> M;
    for(int i=1;i<=n;i++){//两个参数限制
        cin >> v >> m >> w;
        for(int j=V;j>=v;j--){
            for(int k=M;k>=m;k--){//能取: 1.不想取 2.想取
                dp[j][k]=max(dp[j][k],dp[j-v][k-m]+w);
            }
        }
        
    }
    cout << dp[V][M] << endl;
    return 0;
}

分组背包问题

三重循环

背包问题求方案数

思路：g[ i ][ j ]表示前i个商品体积恰好为j的方案数

朴素写法

#include <bits/stdc++.h>

using namespace std;


const int M=1e9+7;
int n,m;
int dp[1005][1005]={0};
int v,w;
int g[1005][1005];//前i个商品体积恰好为j的方案数

int main(){
    
    
    g[0][0]=1;//初始化
    
    cin >> n >> m;
    for(int i=1;i<=n;i++){//01背包
        cin >> v >> w;
        for(int j=0;j<=m;j++){
            
            if(j<v){//取不到
                dp[i][j]=dp[i-1][j];
                g[i][j]=g[i-1][j]%M;
            }else{//能取：1.想取 2.不想取
                int x=dp[i-1][j];
                int y=dp[i-1][j-v]+w;
                
                if(x==y){
                    g[i][j]=(g[i-1][j]+g[i-1][j-v])%M;
                }else if(x>y){
                    g[i][j]=g[i-1][j]%M;
                }else{
                    g[i][j]=g[i-1][j-v]%M;
                }
                
                dp[i][j]=max(x,y);
            }
        }
    }
    
    //注意
    int res=0;
    for(int i=0;i<=m;i++){
        if(dp[n][m]==dp[n][i]){
            res=(res+g[n][i])%M;
        }
    }
    cout << res << endl;
    
     
    return 0;
}

（优化）

#include <bits/stdc++.h>

using namespace std;


const int M=1e9+7;
int n,m;
int dp[1005];
int v,w;
int g[1005];//体积恰好为j的方案数

int main(){
    
    
    g[0]=1;//初始化
    
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> v >> w;
        for(int j=m;j>=v;j--){//01背包
            
            //能取：1.想取 2.不想取
            int x=dp[j];
            int y=dp[j-v]+w;
                
            if(x==y){
                g[j]=(g[j]+g[j-v])%M;
            }else if(x>y){
                g[j]=g[j]%M;
            }else{
                g[j]=g[j-v]%M;
            }
            dp[j]=max(x,y);
        }
    } 
    
    //注意
    int res=0;
    for(int i=0;i<=m;i++){
        if(dp[m]==dp[i]){
            res=(res+g[i])%M;
        }
    }
    cout << res << endl;
    
     
    return 0;
}

求背包问题的方案

注意：我们此时不能将二维数组压缩为一维数组，这是因为数组 dp 中间的状态还需要被使用。

在这里插入图片描述

(1)只能选，则必须选

(2)不能选，则必不选

(3)可选可不选，则必须选，为了字典序最小

#include <bits/stdc++.h>

using namespace std;

int n,m;
int dp[1005][1005]={0};
int v[1005],w[1005];

int main(){
    
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        cin >> v[i] >> w[i];
    }
    
    for(int i=n;i>=1;i--){//逆序遍历  :为了最小字典序
        
        for(int j=0;j<=m;j++){//01背包
            if(j<v[i]){//取不到
                dp[i][j]=dp[i+1][j];
            }else{//能取：1.想取 2.不想取
                dp[i][j]=max(dp[i+1][j],dp[i+1][j-v[i]]+w[i]);
            }
        }
    }
    
    
    int j=m;
    for(int i=1;i<=n;i++){
        if(j>=v[i]&&dp[i][j]==dp[i+1][j-v[i]]+w[i]){
            cout << i << " ";
            j-=v[i];
        }
    }
    cout << endl;
    
    return 0;
}

有依赖的背包问题
略

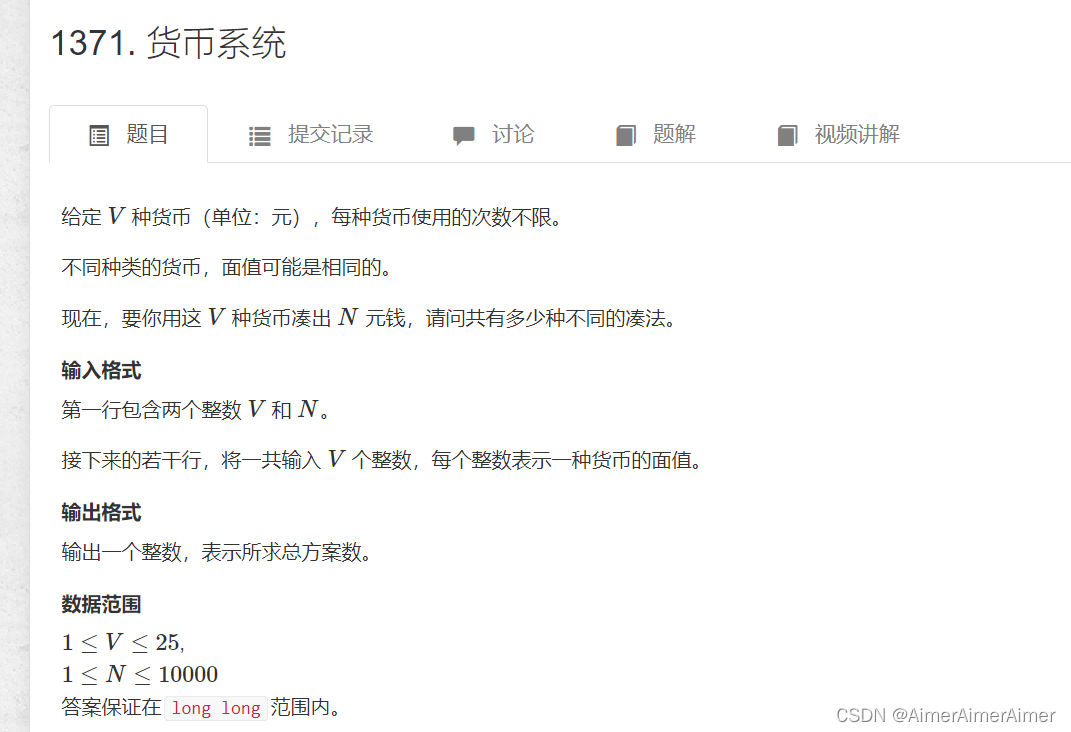
10.货币系统

在这里插入图片描述
二维数组（朴素）

思路：前i种面值恰好凑成面额j的方案数

#include<bits/stdc++.h>
#define ll long long

using namespace std;

int n,m,x;
ll dp[35][10005];//前i种面值恰好凑成面额j的方案数


int main(){


    dp[0][0]=1;//初始化
    cin >> n >> m;
    for(int i=1;i<=n;i++){//完全背包

        cin >> x;
        for(int j=0;j<=m;j++){

            if(j<x){//取不了
                dp[i][j]=dp[i-1][j];
            }else{//能取: 1.不想取 2.想取
                dp[i][j]=dp[i-1][j]+dp[i][j-x];
            }
        }
    }
    
    cout << dp[n][m] << endl;
    return 0;
}

(优化)

#include<bits/stdc++.h>
#define ll long long

using namespace std;

int n,m,x;
ll dp[10005];//恰好凑成面额j的方案数


int main(){

    
    cin >> n >> m;
    
    dp[0]=1;//初始化
    for(int i=1;i<=n;i++){//完全背包

        cin >> x;
        for(int j=x;j<=m;j++){

            //能取: 1.不想取 2.想取
            dp[j]=dp[j]+dp[j-x];
        }
    }
    
    cout << dp[m] << endl;
    return 0;
}