算法实现题 3-5 石子合并问题（区间DP）
题目地址
题目描述：
桌面上从左到右放着 n(1≤n≤200) 堆石子，其中第 i堆石子包含的石子数量为 ai
现在要将石子有序地合并成一堆。
规定每次只能取相邻的两堆石子合并成新的一堆，并将新的一堆的石子数，记为该次合并的花费。
那么，n?1 次合并后，石子将合并成一堆。
你需要寻找一种合并方案，使得花费总和最小。输出最小的花费总和。
输入格式：
输入的第一行包含一个整数 n(1≤n≤200)，用于表示石子堆数。
输入的第二行包含 n 个整数，以空格间隔，分别表示初始时每一堆的石子数。
输出格式:
输出一个整数，用于表示将 n 堆石子合并成一堆的最小花费。
输入输出样例
输入
5
1 3 2 4 5
输出
34
算法分析：
对于动态规划问题首先找出它的状态转移方程：
对于最小得分：
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]) 条件：j!=i
对于最大得分：
dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]) 条件：j!=i
对于i=j时 其实就相当于就一堆 dp[i][j]=0;
方程解释：
dp[i][j]: 合并第i堆石子到第j队石子所用的最大(小)得分或者说合并[i，j]这个区间范围内的石子最大/小花费总和
sum数组是前缀和，sum[i]表示一个数组从下标为0到下标为i之间所有的数据和
sum[i]=sum[i-1]+a[i]
想要更详细的请参考这位大哥👉前缀和👈
dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1] 其中的k参数代表从i到j的上一次合并是从k分开的，也就是上一步状态是从i->k，k+1->j（不懂看下图）合并成一堆在加上a[i]+a[i+1]+a[i+2]···a[j]用前缀和表示就是sum[j]-sum[i-1]
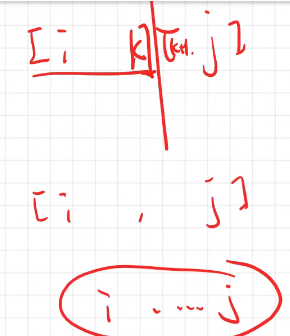
dp[i][j]像这种每个状态都对应一个区间这类问题有专门的称呼---->区间DP
可以通过区间短的状态推导出区间长的状态//决策单调性
从len=1的f[i][i]可以推出len=2的f[i][i+1]
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
const int maxn=220;
int n ,a[maxn],sum[maxn],f[maxn][maxn];
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
scanf("%d",a+i);
sum[i]=sum[i-1]+a[i];
}
memset(f,INF,sizeof(f));
for(int len=1;len<=n;len++)//区间长度
{
for(int i=1;i+len-1<=n;i++)//[i,j]区间起点终点
{
int j=i+len-1;//终点
if(len==1)
f[i][j]=0;
else{
for(int k=i;k<j;k++)
f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+sum[j]-sum[i-1]);
}
}
}
cout<<f[1][n]<<endl;
}
