Morris遍历
一种遍历二叉树的方式,并且时间复杂度O(N),额外空间复杂度O(1),通过利用原树中大量空闲指针的方式,达到节省空间的目的。
morris遍历是二叉树遍历算法的超强进阶算法,跟递归、非递归(栈实现)的空间复杂度相比,morris遍历可以将非递归遍历中的空间复杂度降为O(1)。从而实现时间复杂度为O(N),而空间复杂度为O(1)的精妙算法。
morris遍历利用的是树的叶节点左右孩子为空(树的大量空闲指针),实现空间开销的极限缩减。
Morris遍历细节:
假设来到当前节点cur,开始时cur来到头节点位置
1)如果cur没有左孩子,cur向右移动(cur=cur.right)
2)如果cur有右孩子,找到左子树上最右的节点mostRight:
? ? ? ? a. 如果mostRight的右指针指向空,让其指向cur,然后cur向左移动(cur =cur.left)
? ? ? ? b. 如果mostRight的右指针指向cur,让其指向null, 然后cur向右移动(cur=cur.right)
3) cur为空时遍历停止
示例:
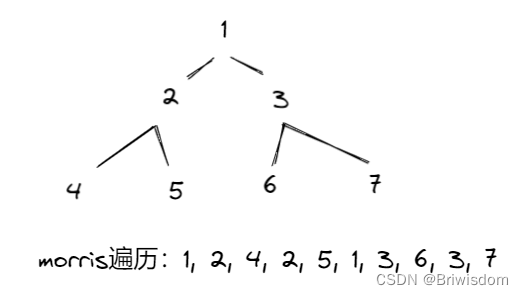
相比递归版本的遍历,每个节点最多会经过3次,而Morris遍历最多经过2次。
public static class Node
{
public int value;
Node left;
Node right;
public Node(int data)
{
this.value =data;
}
}
//递归调用
public static void process(Node head)
{
if(head ==null)
{
return;
}
//1,打印位置,中序遍历
//System.out.println(head.value + " ");
process(head.left);
//2,打印位置,先序遍历
//System.out.println(head.value + " ");
process(head.right);
//3,打印位置,后序遍历
//System.out.println(head.value + " ");
}
//morris调用
public static void morris(Node head)
{
if (head ==null)
{
return;
}
Node cur=head;
Node mostRight =null;
while(cur !==null)
{
mostRight =cur.left;
if (mostRight !=null)
{
while(mostRight.right !=null && mostRight.right !=cur)
{
mostRight=mostRight.right;
}
if (mostRight.right ==null)
{
mostRight.right ==cur;
cur=cur.left;
continue;
}
else
{
mostRight.right==null;
}
cur =cur.right;
}
}
}morris方法分别实现先序遍历,中序遍历,后续遍历的话,修改思路:
先序遍历:
节点出现一次,直接打印
节点出现两次,第一次时候才打印
中序遍历:
节点只出现一次,直接打印
节点出现两次,第二次打印
后序遍历:
先对出现2次的节点,逆序打印左树右边界
最后逆序打印整棵树右边界
//先序遍历
public static void morrisPre(Node head) {
if(head == null){
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null){
// cur表示当前节点,mostRight表示cur的左孩子的最右节点
mostRight = cur.left;
if(mostRight != null){
// cur有左孩子,找到cur左子树最右节点
while (mostRight.right !=null && mostRight.right != cur){
mostRight = mostRight.right;
}
// mostRight的右孩子指向空,让其指向cur,cur向左移动
if(mostRight.right == null){
mostRight.right = cur;
System.out.print(cur.value+" ");
cur = cur.left;
continue;
}else {
// mostRight的右孩子指向cur,让其指向空,cur向右移动
mostRight.right = null;
}
}else {
System.out.print(cur.value + " ");
}
cur = cur.right;
}
System.out.println();
}
//中序遍历
public static void morrisIn(Node head) {
if(head == null){
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null){
mostRight = cur.left;
if(mostRight != null){
while (mostRight.right !=null && mostRight.right != cur){
mostRight = mostRight.right;
}
if(mostRight.right == null){
mostRight.right = cur;
cur = cur.left;
continue;
}else {
mostRight.right = null;
}
}
System.out.print(cur.value+" ");
cur = cur.right;
}
System.out.println();
}
//后序遍历
public static void morrisPos(Node head) {
if(head == null){
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null){
mostRight = cur.left;
if(mostRight != null){
while (mostRight.right !=null && mostRight.right != cur){
mostRight = mostRight.right;
}
if(mostRight.right == null){
mostRight.right = cur;
cur = cur.left;
continue;
}else {
mostRight.right = null;
printEdge(cur.left);
}
}
cur = cur.right;
}
printEdge(head);
System.out.println();
}
public static void printEdge(Node node){
Node tail =reverseEdge(node);
Node cur = tail;
while (cur != null ){
System.out.print(cur.value+" ");
cur =cur.right;
}
reverseEdge(tail);
}
public static Node reverseEdge(Node node){
Node pre = null;
Node next = null;
while (node != null){
next = node.right;
node.right = pre;
pre = node;
node = next;
}
return pre;
}
