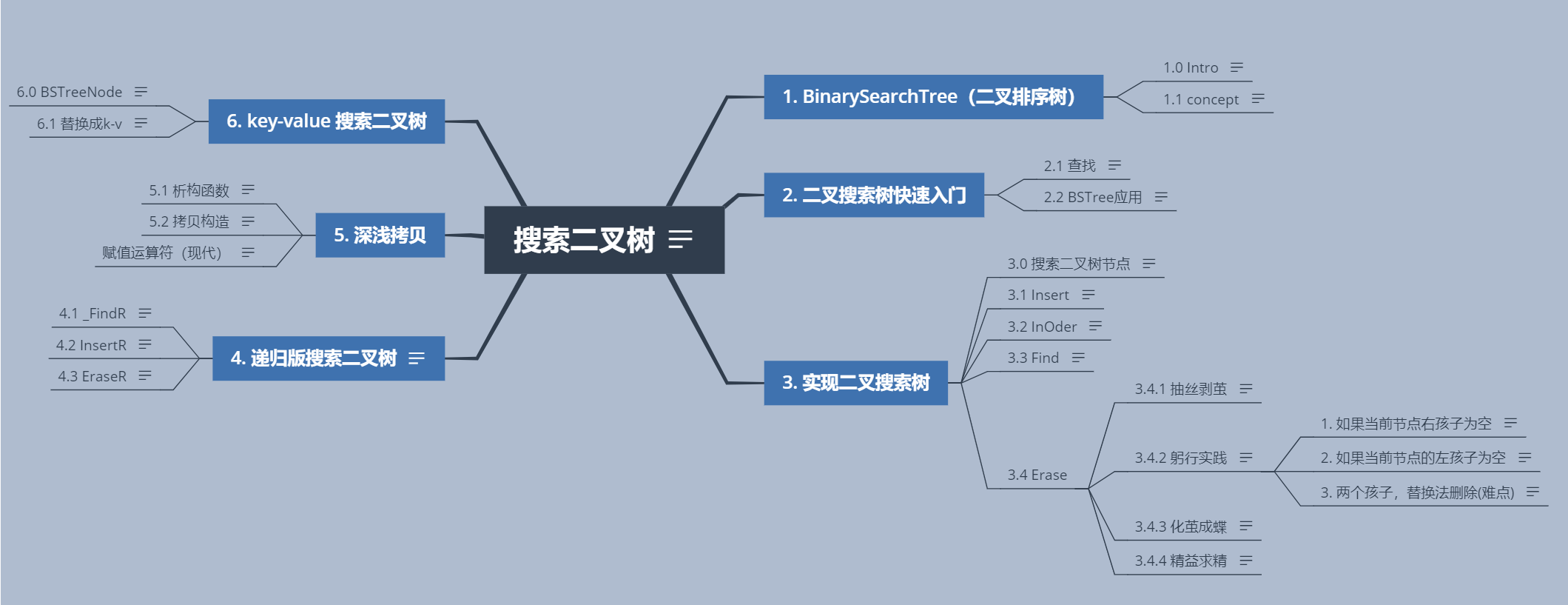
请回答数据结构【二叉搜索树】
1. BinarySearchTree(二叉排序树)
1.0 Intro
二叉搜索树也是一种树形结构,map和set的特性就需要用到二叉搜索树
搜索二叉树的增删查改时间复杂度是O(N)
1.1 concept
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
🌸 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
🌸 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
🌸 它的左右子树也分别为二叉搜索树
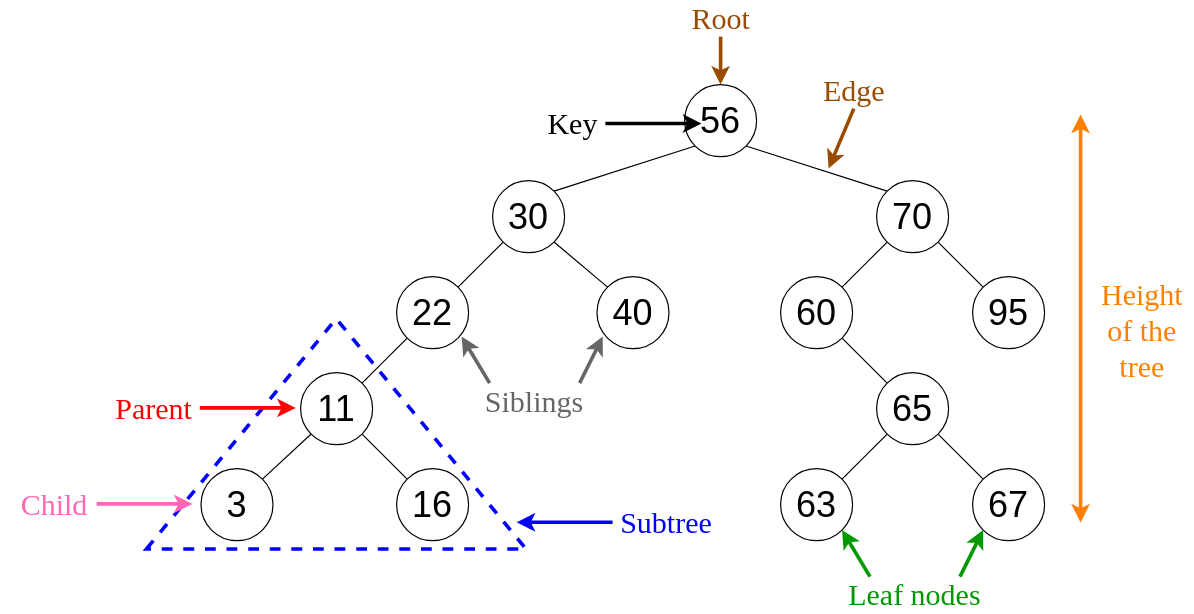
picture is from https://faun.pub/introduction-to-binary-search-trees-8e225aca7037
2. 二叉搜索树快速入门
2.1 查找
最坏查找高度次,就可以确认一个值在不在树中
查找时间复杂度O(N)
极端:单支
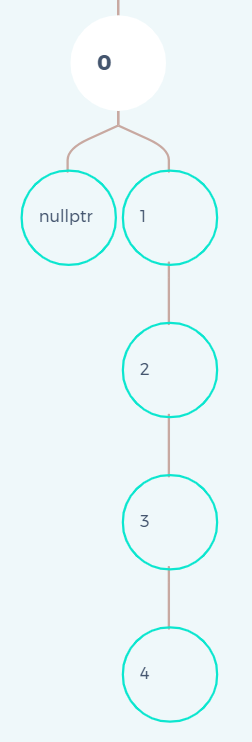
所以实际使用中一般还是没办法保证极度情况下的效率
于是人们在搜索二叉树的特性上扩展延申,产生了:AVLTree和红黑树
这些树堆左右高度有所要求,非常接近完全二叉树,他们的效率可以达到O(logN),
如果不是对于内存查找有所要求的话,有时候还会对磁盘查找有所要求,于是我们对树的高度又提出要求进而衍生出了B树系列,适合于外查找存储
2.2 BSTree应用
🍁 K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
🍁 KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。
3. 实现二叉搜索树
3.0 搜索二叉树节点
如果你要把他叫成搜索二叉树的话你可以把结构typedef成SBTree,但是属实是不太好
我们通过用struct构造一个Node,然后封装入BSTree中,为了方便,将BSTreeNode<K> typedef 成 Node
template<class K>
struct BSTreeNode
{
//字段
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
//构造
BSTreeNode(const K& key)
: _left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{}
};
3.1 Insert
下面来实现插入,插入的话显示遍历,找到插入位置,然后链接cur节点它不是很难
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
else
{
//非递归
Node* cur = _root;
Node* parent = nullptr;
//1. 遍历到底
while (cur)
{//插入一个值之后还要来链接节点,链接父亲
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else//相等 -> return false
return false;
}
//2. 链接cur节点
cur = new Node(key);
if (parent->_key<key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
}
3.2 InOder
这里选择中序遍历的原因是可以在输出的时候保证数据大小是有规律的,毕竟有着搜索二叉树的特性,就是左子树<根节点<右子树
这里的InOder为了防止传参要传根节点参数,我们可以封装一下,这样就不用传参了
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
//防止传参要传根节点,我们可以封装一下
void InOder()
{
_InOrder(_root);
}
3.3 Find
查找,很简单
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
cur = cur->_right;
else if (cur->_key>key)
cur = cur->_left;
else
return cur;
}
return nullptr;
}
3.4 Erase
3.4.1 抽丝剥茧
删除一个节点不管怎样删除完了一定还要保证是搜索二叉树就是宗旨
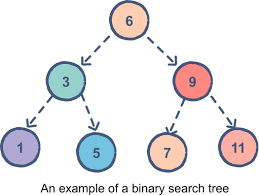
🍒 1. 如果要删除的是 1 5 7 11 的话其实相对好处理,特征是叶子节点
🌸 注意父亲节点的left或者tight也要置空,因为我们不想要野指针
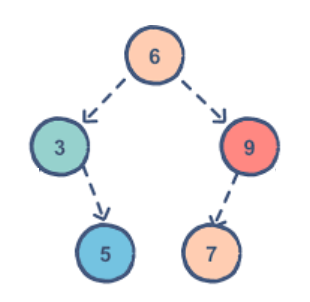
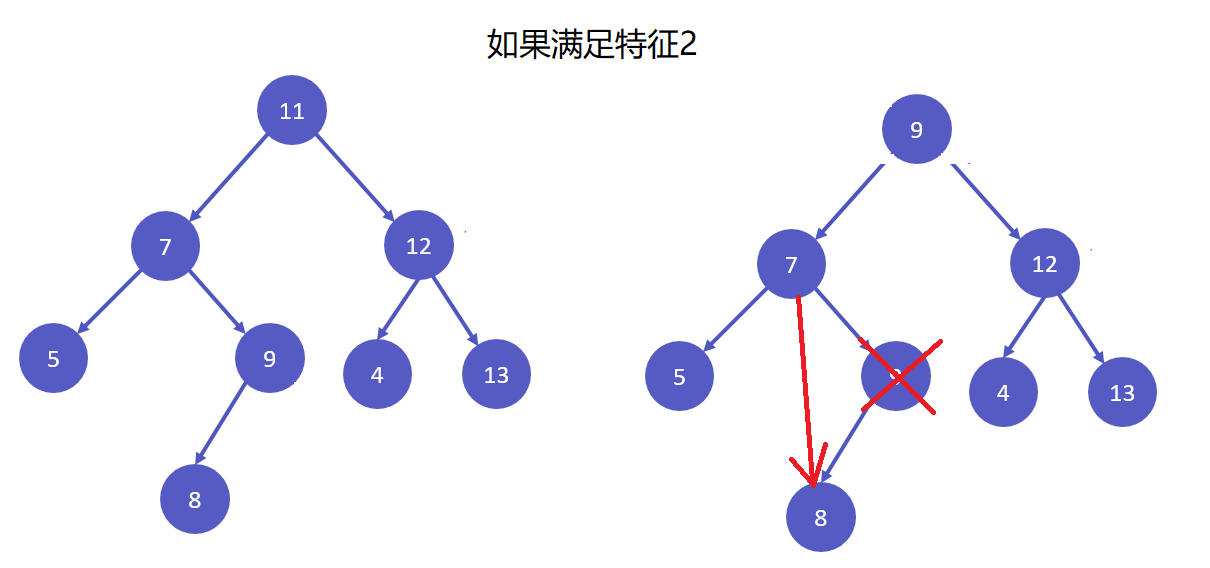
🍒 2. 如果是如果要删除的节点是 3 9 就相对麻烦一点,特征是:只有一个孩子
🌸 那我删除完之后交给父亲管理就可以了,然后父亲只要把指向自己位置的指针顶替即可
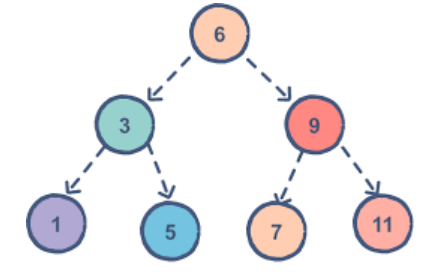
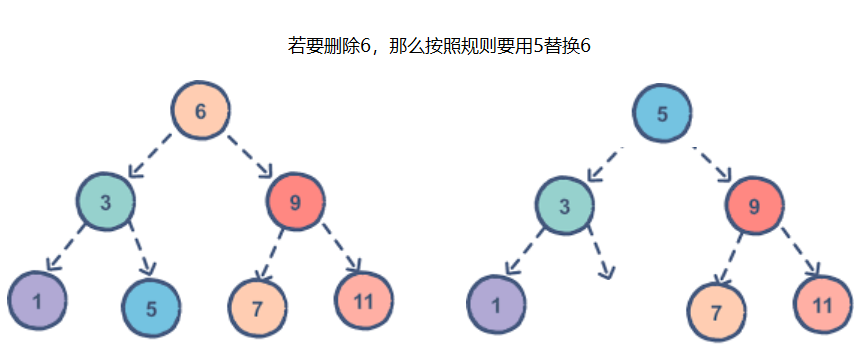
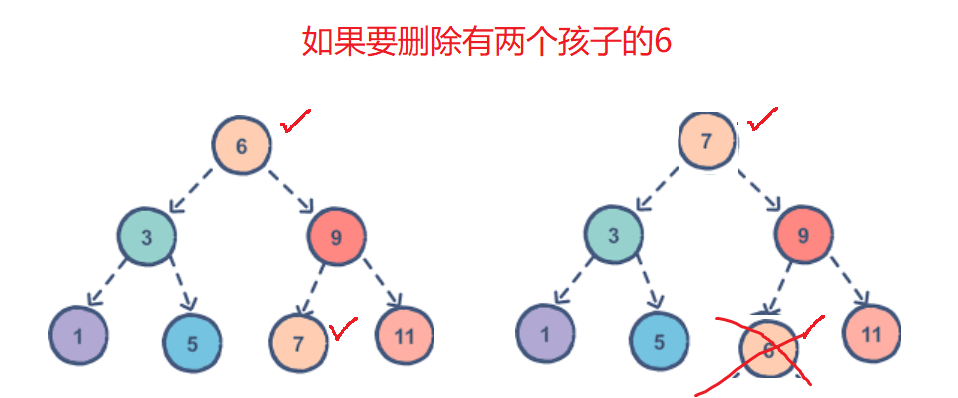
🍒 3. 如果要删除的是当前情况下的 3 6 9 就不好处理了,特征是:有两个孩子
🌸 解决方案就是替换删除,从孩子中找一个能够替换自己的节点,替换删除,只有比左边大比右边小才可以,那么这个孩子怎么找?
🌿 左子树的最大节点,左子树最右节点就是最大的
🌿 右子树的最小节点,右子树最左节点就是最小的
🍁 这两个节点去替换后,都符合特征2或特征1的可以直接删除
满足特征1,我要删除6
满足特征2,我要删除11
继续分析,特征1的其实可以当成特征2去处理,简化一点
3.4.2 躬行实践
下面来仔细分析删除,同样的还是要定义父亲指针和孩子指针
当找到要删除的节点,然后开始判断
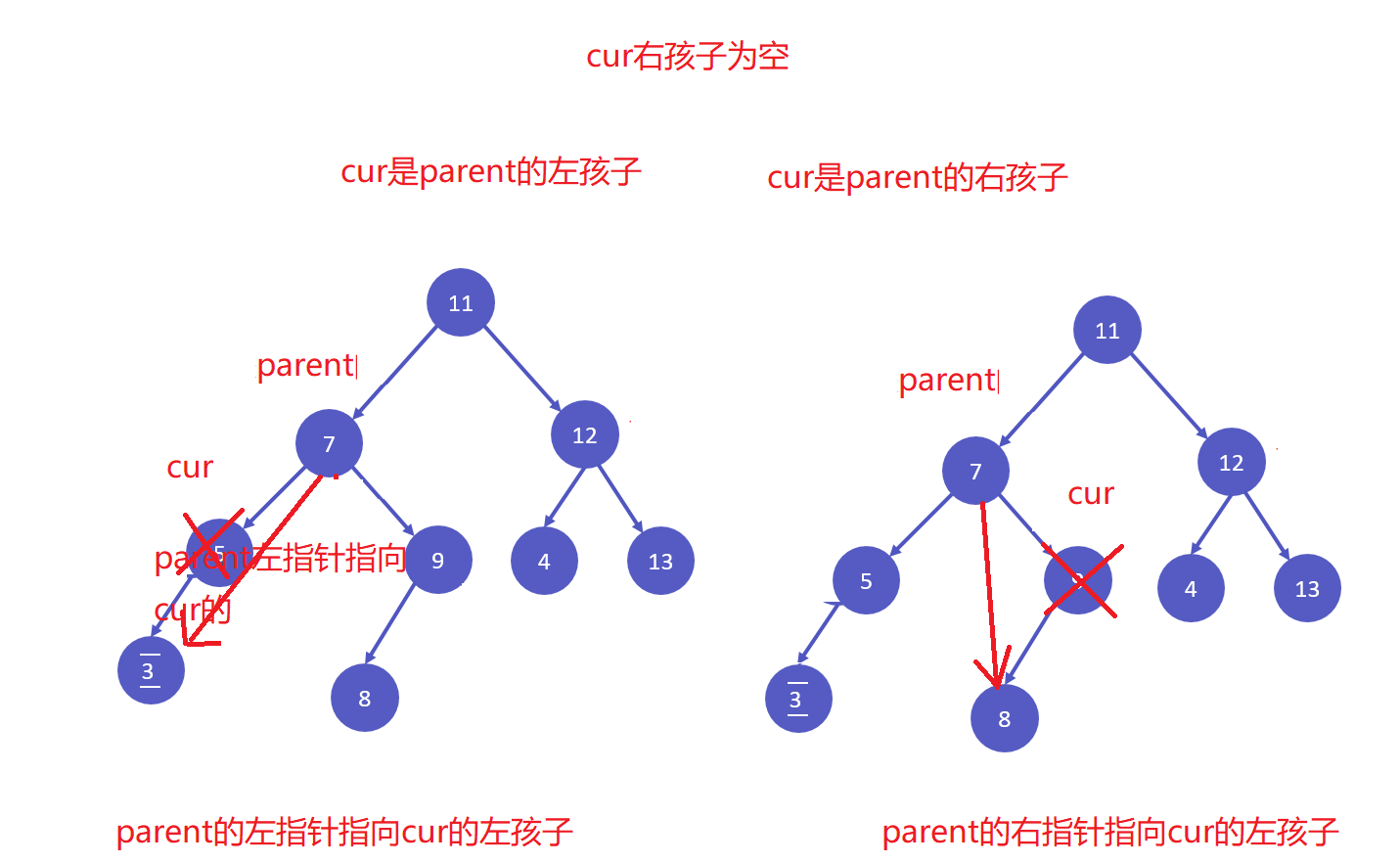
- 如果当前节点右孩子为空
else if (cur->_right == nullptr)
{
if (parent->_left == cur)
{//我是父亲的左
parent->_left = cur->_left;
}
else
{//我是父亲的右
parent->_right = cur->_left;
}
delete cur;
}
- 如果当前节点的左孩子为空
和上图同理
if (cur->_left==nullptr)
{//父亲指向cur的右
if (parent->_left == cur)
{//我是父亲的左
parent->_left = cur->_right;
}
else
{//我是父亲的右
parent->_right = cur->_right;
}
delete cur;//置空节点
}
- 两个孩子,替换法删除(难点)
我们假设采取右树的最左节点来替换(也可以左树的最右节点)
else
//两个孩子,替换法删除
{
Node* min_parent = nullptr;
Node* minRight = cur->_right;
//找到右树的最左节点
while (minRight->_left)
{
min_parent = minRight;
minRight = minRight->_left;
}
//保存替换的节点
cur->_key = minRight->_key;
//删除替换节点
min_parent->_left = minRight->_right;
delete minRight;
}
还有问题存在,极端情况下,如果我要删除的是下面的7的话
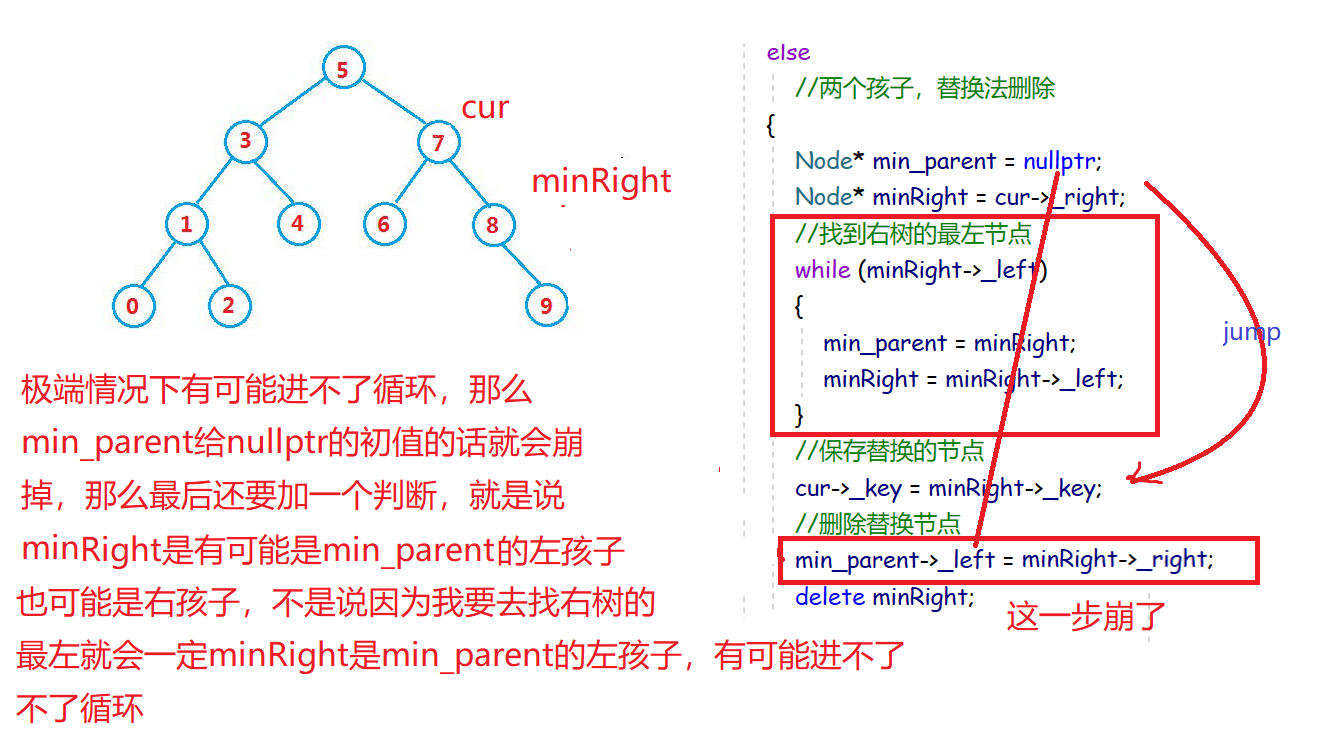
else
//两个孩子,替换法删除
{
Node* min_parent = cur;
Node* minRight = cur->_right;
//找到右树的最左节点
while (minRight->_left)
{
min_parent = minRight;
minRight = minRight->_left;
}
//保存替换的节点
cur->_key = minRight->_key;
//删除替换节点
if (min_parent->_left == minRight)
min_parent->_left = minRight->_right;
else
min_parent->_right = minRight->_right;
delete minRight;
}
3.4.3 化茧成蝶
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
//1. 开始找
while (cur)
{
if (cur->_key< key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{//2. 找到了,准备开始删除
//左为空,右为空,都可以,把孩子交给父亲管理
if (cur->_left==nullptr)
{//父亲指向cur的右
if (parent->_left == cur)
{//我是父亲的左
parent->_left = cur->_right;
}
else
{//我是父亲的右
parent->_right = cur->_right;
}
delete cur;//置空节点
}
else if (cur->_right == nullptr)
{
if (parent->_left == cur)
{//我是父亲的左
parent->_left = cur->_left;
}
else
{//我是父亲的右
parent->_right = cur->_left;
}
delete cur;
}
else
//两个孩子,替换法删除
{
Node* min_parent = cur;
Node* minRight = cur->_right;
//找到右树的最左节点
while (minRight->_left)
{
min_parent = minRight;
minRight = minRight->_left;
}
//保存替换的节点
cur->_key = minRight->_key;
//删除替换节点
if (min_parent->_left == minRight)
min_parent->_left = minRight->_right;
else
min_parent->_right = minRight->_right;
delete minRight;
}
return true;
}
}
return false;
}
3.4.4 精益求精
完了吗,就这样吗,太麻烦了,还可以改简单一点,为什么不复用呢?当然复用的话会慢一点,因为要再查找一次
else
//两个孩子,替换法删除
{
//找到右树的最左节点
Node* minRight = cur->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
K min = minRight->_key;
//递归去删除替换节点,一定会走到作为空的情况处理
this->Erase(min);
cur->_key = min;//先删除再替换
}
还有就是发现删光树的时候崩掉了,说明还有问题

bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
//1. 开始找
while (cur)
{
if (cur->_key< key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{//2. 找到了,准备开始删除
//左为空,右为空,都可以,把孩子交给父亲管理
if (cur->_left==nullptr)
{
//如果cur没有父亲
if (cur == _root)
{
_root = cur->_right;
}
else
{
//父亲指向cur的右
if (parent->_left == cur)
{//我是父亲的左
parent->_left = cur->_right;
}
else
{//我是父亲的右
parent->_right = cur->_right;
}
}
delete cur;//置空节点
}
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{//我是父亲的左
parent->_left = cur->_left;
}
else
{//我是父亲的右
parent->_right = cur->_left;
}
}
delete cur;
}
else
//两个孩子,替换法删除
{
Node* minRight = cur->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
K min = minRight->_key;
//递归去删除替换节点,一定会走到作为空的情况处理
this->Erase(min);
cur->_key = min;//先删除再替换
}
return true;
}
}
return false;
}
4. 递归版搜索二叉树
之前的是非递归版搜索二叉树,现在来写一下递归版本的,为了控制递归的参数,我们采用了函数封装一个多参数版的递归用_函数,并将其放到了private中私有化,不让其他人调用
4.1 _FindR
private:
Node* _FindR(Node* root, const K& key)
{
//如果为空
if (root==nullptr)
return nullptr;
//如果不为空
if (root->_key>key)
return _FindR(root->_left,key);
else if(root->_key<key)
return _FindR(root->_right,key);
else
return _root;
}
public:
Node* FindR(const K& key)
{//为了递归保证参数
return _FindR(_root, key);
}
4.2 InsertR
插入的时候需要我们的思考,究竟什么时候我们怎么把要插入节点的父亲和孩子连上
其实很简单一个操作就可以解决了,就是把参数写成Node*& root,看看引用的效果
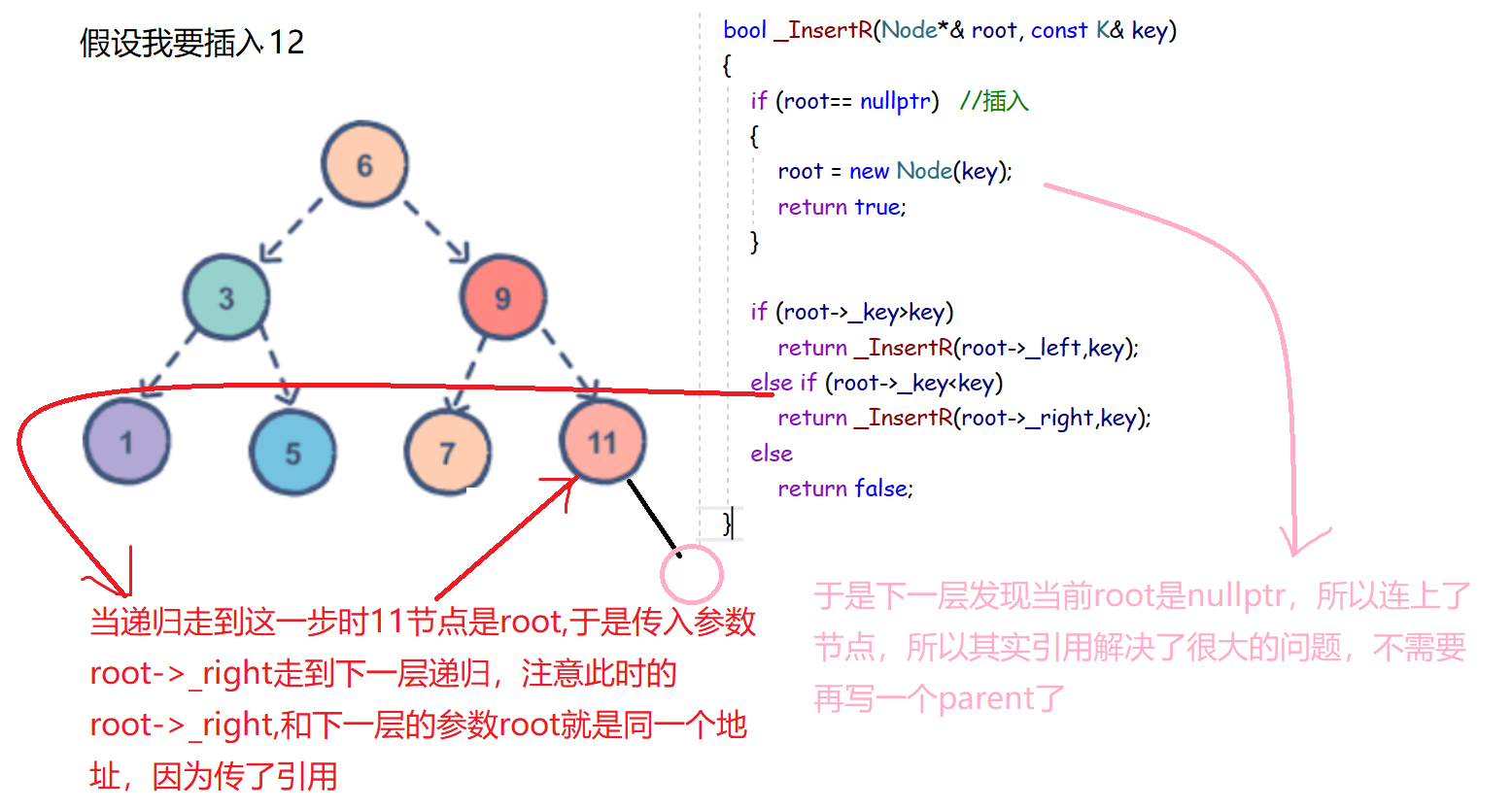
private:
bool _InsertR(Node*& root, const K& key)
{
if (root== nullptr) //插入
{
root = new Node(key);
return true;
}
if (root->_key>key)
{
return _InsertR(root->_left,key);
}
else if (root->_key<key)
{
return _InsertR(root->_right,key);
}
else
{
return false;
}
}
public:
bool InsertR(const K& key)
{
return _InsertR(root, key);
}
4.3 EraseR
先去找要删除的节点
//找不到返回false
if (root==nullptr)
return false;
//寻找该节点
if (root->_key < key)
return _EraseR(root->_right, key);
else if (root->_key > key)
return _EraseR(root->_left, key);
else{}
找到之后开始删除,删除之前保存一下指针,指向原来的root,然后就可以delete了
//找到了,要删除root
if (root->_left==nullptr)
{//左树空,右树存在
Node* del = root;//当下要删除的保存一下过会删除
root = root->_right;//找到删掉节点的右孩子
delete del;//删除节点
}
else if(root->_right==nullptr)
{//右树空,左树存在
Node* del = root;
root = root->_left;
delete del;
}
对于两个孩子的情况,替代法的话是用不上别名的,无法借助别名的话, 可以去最朴素的方法去删除,就还是原来非递归的写法
也可以用复用法,这里提供一下复用法
else
{//两孩子都存在,找右树的最左子代
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
K min = minRight->_key;
// 转换成在root的右子树删除min
_EraseR(root->_right, min);
root->_key = min;
}
那么整体来就是
bool _EraseR(Node*& root, const K& key)
{
if (root==nullptr)
return false;
//寻找该节点
if (root->_key < key)
return _EraseR(root->_right, key);
else if (root->_key > key)
return _EraseR(root->_left, key);
else
{//找到了,要删除root
if (root->_left==nullptr)
{//左树空,右树存在
Node* del = root;//当下要删除的保存一下过会删除
root = root->_right;//找到删掉节点的右孩子
delete del;//删除节点
}
else if(root->_right==nullptr)
{//右树空,左树存在
Node* del = root;
root = root->_left;
delete del;
}
else
{//两孩子都存在,找右树的最左子代
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
K min = minRight->_key;
// 转换成在root的右子树删除min
_EraseR(root->_right, min);
root->_key = min;
}
return true;
}
}
5. 深浅拷贝
5.1 析构函数
private:
//封装析构
void _Destroy(Node* root)
{//后序遍历析构
if (root==nullptr)
return;
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
}
public:
~BSTree()
{
_Destroy(_root);
_root = nullptr;
}
5.2 拷贝构造
private:
Node* _Copy(Node* root)
{
if (root==nullptr)
{
return nullptr;
}
Node* copyNode = new Node(root->_key);
copyNode->_left = _Copy(root->_left);
copyNode->_right = _Copy(root->_right);
return copyNode;
}
public:
BSTree(const BSTree<K>& tree)
{
//递归拷贝
_root=_Copy(tree._root);
}
赋值运算符(现代)
//赋值运算符
//t1=t2
BSTree<K>& operator=(BSTree<K> tree)
{
swap(_root, tree._root);
return *this;
}
6. key-value 搜索二叉树
6.0 BSTreeNode
template<class K,class V>
struct BSTreeNode
{
BSTreeNode<K,V>* _left;
BSTreeNode<K,V>* _right;
K _key;
V _value;
BSTreeNode(const K& key, const V& value)
: _left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value);
{}
};
6.1 替换成k-v
template<class K,class V>
class BSTree
{
typedef BSTreeNode<K,V> Node;
//下面的有些封装的函数可以放在私有的, 别人最好无法调用
private:
//封装析构
void _Destroy(Node* root )
{//后序遍历析构
if (root == nullptr)
return;
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
}
//封装拷贝构造
Node* _Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* copyNode = new Node(root->_key);
copyNode->_left = _Copy(root->_left);
copyNode->_right = _Copy(root->_right);
return copyNode;
}
Node* _FindR(Node* root, const K& key)
{
//如果为空
if (root == nullptr)
return nullptr;
//如果不为空
if (root->_key > key)
return _FindR(root->_left, key);
else if (root->_key < key)
return _FindR(root->_right, key);
else
return _root;
}
//不许相同节点
bool _InsertR(Node*& root, const K& key, const V& value)
{
if (root == nullptr) //插入
{
root = new Node(key,value);
return true;
}
if (root->_key > key)
return _InsertR(root->_left, key,value);
else if (root->_key < key)
return _InsertR(root->_right, key,value);
else
return false;
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
//寻找该节点
if (root->_key < key)
return _EraseR(root->_right, key);
else if (root->_key > key)
return _EraseR(root->_left, key);
else
{//找到了,要删除root
if (root->_left == nullptr)
{//左树空,右树存在
Node* del = root;//当下要删除的保存一下过会删除
root = root->_right;//找到删掉节点的右孩子
delete del;//删除节点
}
else if (root->_right == nullptr)
{//右树空,左树存在
Node* del = root;
root = root->_left;
delete del;
}
else
{//两孩子都存在,找右树的最左子代
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
K k_min = minRight->_key;
V v_min = minRight->_value;
// 转换成在root的右子树删除min
_EraseR(root->_right, k_min);
root->_key = k_min;
root->_value = v_min;
}
return true;
}
}
public:
BSTree()
:_root(nullptr)
{}
//析构
~BSTree()
{
_Destroy(_root);
_root = nullptr;
}
//拷贝构造
BSTree(const BSTree<K,V>& tree)
{
//递归拷贝
_root = _Copy(tree._root);
}
//赋值运算符
//t1=t2
BSTree<K,V>& operator=(BSTree<K,V> tree)
{
swap(_root, tree._root);
return *this;
}
bool InsertR(const K& key,const V& value)
{
return _InsertR(_root, key,value);
}
Node* FindR(const K& key)
{//为了递归保证参数
return _FindR(_root, key);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " : " << root->_value << endl;
_InOrder(root->_right);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
Node* _root;
};
有关代码放到代码仓库了https://github.com/Allen9012/cpp/tree/main/C%2B%2B%E8%BF%9B%E9%98%B6/BSTree
后序会更一些有关二叉树的OJ题