一、概述

??模拟退火算法（Simulated Annealing，SA）是一种模拟物理退火过程而设计的优化算法。它的基本思想最早在1953年就被Metropolis提出，但直到1983年，Kirkpatrick等人才设计出真正意义上的模拟退火算法并进行应用。
??模拟退火算法采用类似于物理退火的过程。先在一个高温状态下，然后逐渐退火，在每个温度下慢慢冷却，最终达到物理基态（相当于算法找到最优解）。模拟退火算法源于对固体退火过程的模拟，采用Metropolis准则，并用一组称为冷却进度表的参数控制算法的进程，使得算法在多项式时间里可以给出一个近似最优解。
??模拟退火算法在某一初温下，伴随温数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解。即在局部最优解的空间内能概率性地跳出并最终趋于全局最优。

二、模拟退火算法

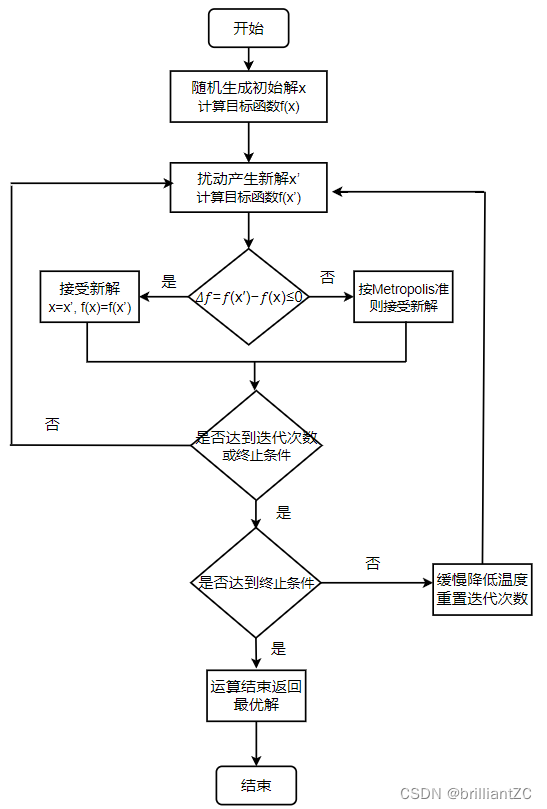
一、算法的主要流程：

step1: 设定当前解（即为当前的最优解)：令 $T$ = $T_0$ ，即开始退火的初始温度，随机生成一个初始解 $x_0$ ，并计算相应的目标函数值E( $x_0$ )。
step2: 产生新解与当前解差值：根据当前解 $x_i$ 进行扰动，产生一个新解 $x_j$ ，计算相应的目标函数值E( $x_j$ ),得到𝜟𝑬=𝑬( $x_j$ )?𝑬( $x_i$ )。
step3: 判断新解是否被接受：若𝜟𝑬<𝟎，则新解 $x_j$ 被接受；若𝜟𝑬>𝟎 ，则新解 $x_j$ 按概率e $-(𝑬(x_j)?𝑬(x_i)) \over T_i$ 接受， $T_i$ 为当前温度。
step4: 当新解被确定接受时：新解 $x_j$ 被作为当前解
step5: 循环以上四个步骤：在温度 $T_i$ 下，重复k次的扰动和接受过程，接着执行下一步骤。
step6: 最后找到全局最优解：判断T是否已经达到终止温度 $T_f$ ，是，则终止算法；否，则转到循环步骤继续执行。

二、冷却进度表

??退火过程由一组初始参数，即冷却进度表控制。它的目的是尽量使系统达到平衡，以使算法在有限的时间内逼近最优解。它包括：

1.控制温度参数的初值 $T_0$
??一般来说，只有足够大的才能满足算法要求，但是由于不同问题处理的规模不同，所以这个“足够大”也是不同的，有的可能 $T_0$ =100就好了，但是有的可能 $T_0$ =1000还不够。实验表明：初温越大，获得全局最优解的机率越大，但花费的时间也会越长。

Metropolis准则：
??在某个温度下固体分子从一个状态转移到另一个状态时，如果新状态的内能小，则无条件接受；如果新状态的内能大，则以一定的概率接受它。

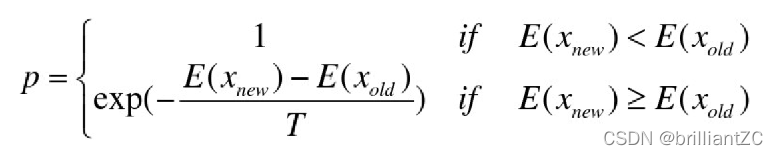
2.马尔科夫链的长度 $L_k$ ：任意温度T的迭代次数
??算法在马尔科夫链长度内持续进行”产生新解—判断—接受/舍弃”的迭代过程，对应着固体在某一恒定温度下趋于热平衡的过程。若在一定的温度下做无限次迭代，相应的马尔科夫链可以达到平稳分布概率。
??马尔科夫链的选取还与温度控制参数 $T_k$ 的下降密切相关，缓慢下降可以避免过长的马尔科夫链。在控制参数的衰减函数已经选定的前提下，让每个取值都能够达到准平衡状态。
??根据这一原则一般取 $L_k$ =100N，其中N为问题的规模。

3. 控制参数T的终值 $T_f$ （停止准则）：
??合理的停止准则既能保证算法收敛于某一近似解,又能使最终解具有一定的全局性。通常可以根据迭代的次数或者终止的温度或者迭代过程在若干个相继的链中的解没有任何变化等条件来判断迭代的终止。
??最终温度通常是0，但会耗掉许多模拟时间。温度趋近于0，其周围状态几乎是一样的。所以找寻一个低到可接受的温度即可。

4. 控制温度T的衰减函数(温度的更新)
?? 不同退火方法的温度下降速度是不一样的,其中指数降温是最常用的一种退火策略,其温度变化很有规律,直接与参数相关,衰减函数：t $_k$ + $_1$ =α $t_k$ ，k=0，1，2… 其中α是一个接近1的常数。一般取0.5~0.99。该衰减函数对控制参数的衰减量是随算法进程递减的。

注意：小的衰减量可能导致算法进程迭代次数的增加,从而使算法进程接受更多的变换,从而访问更多的邻域,搜索更大范围的解空间,返回更高质量的最终解。

三、算法的优缺点

?? 模拟退火算法的应用很广泛，可以高效地求解NP完全问题，如货郎担问题(Travelling Salesman Problem，简记为TSP)、最大截问题(Max Cut Problem)、0-1背包问题(Zero One Knapsack Problem)、图着色问题(Graph Colouring Problem)等等，但其参数难以控制，不能保证一次就收敛到最优值，一般需要多次尝试才能获得（大部分情况下还是会陷入局部最优值）。观察模拟退火算法的过程，具有以下主要优势：

迭代搜索效率高，并且可以并行化；
算法中有一定概率接受比当前解较差的解，因此一定程度上可以跳出局部最优；
算法求得的解与初始解状态S无关，因此有一定的鲁棒性；
具有渐近收敛性，已在理论上被证明是一种以概率l 收敛于全局最优解的全局优化算法。

三、python实现

代码我参考了别人的代码，如下

import numpy as np

# =================初始化参数===============
D = 10  # 变量维数
Xs = 20  # 上限
Xx = -20  # 下限
# ====冷却表参数====
L = 200  # 马可夫链长度 #在温度为t情况下的迭代次数
K = 0.95  # 衰减参数
S = 0.01  # 步长因子
T = 100  # 初始温度
YZ = 1e-7  # 容差
P = 0  # Metropolis过程中总接受点
# ====随机选点初值设定====
PreX = np.random.uniform(size=(D, 1)) * (Xs - Xx) + Xx
PreBestX = PreX  # t-1代的全局最优X
PreX = np.random.uniform(size=(D, 1)) * (Xs - Xx) + Xx
BestX = PreX  # t时刻的全局最优X

# ==============目标函数=============
def func1(x):
    return np.sum([i ** 2 for i in x])

# ====每迭代一次退火一次(降温), 直到满足迭代条件为止===
deta = np.abs(func1(BestX) - func1(PreBestX))  # 前后能量差

trace = []  # 记录
while (deta > YZ) and (T > 0.1):  # 如果能量差大于允许能量差 或者温度大于阈值
    T = K * T  # 降温

    # ===在当前温度T下迭代次数====
    for i in range(L):  #
        # ====在此点附近随机选下一点=====
        NextX = PreX + S * (np.random.uniform(size=(D, 1)) * (Xs - Xx) + Xx)
        # ===边界条件处理
        for ii in range(D):  # 遍历每一个维度
            while NextX[ii] > Xs or NextX[ii] < Xx:
                NextX[ii] = PreX[ii] + S * (np.random.random() * (Xs - Xx) + Xx)

        # ===是否全局最优解 ===
        if (func1(BestX) > func1(NextX)):
            # 保留上一个最优解
            PreBestX = BestX
            # 此为新的最优解
            BestX = NextX

        # ====Metropolis过程====
        if (func1(PreX) - func1(NextX) > 0):  # 后一个比前一个好
            # 接受新解
            PreX = NextX
            P = P + 1
        else:
            changer = -1 * (func1(NextX) - func1(PreX)) / T
            p1 = np.exp(changer)
            # 接受较差的解
            if p1 > np.random.random():
                PreX = NextX
                P = P + 1
        trace.append(func1(BestX))
    deta = np.abs(func1(BestX) - func1(PreBestX))  # 修改前后能量差

print('最小值点\n', BestX)
print('最小值\n', func1(BestX))