MatLab非线性规划问题—服务中心选址问题
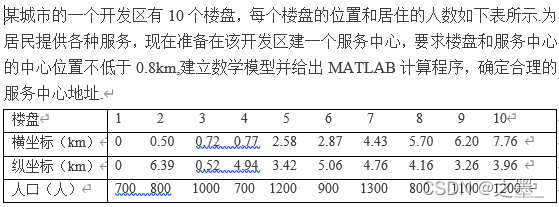
某城市的一个开发区有10个楼盘,每个楼盘的位置和居住的人数如下表所示,为
居民提供各种服务,现在准备在该开发区建一个服务中心,要求楼盘和服务中心
的中心位置不低于0.8km,建立数学模型并给出MATLAB计算程序,确定合理的
服务中心地址
建立数学模型:
楼盘位置用(x,y)表示,人口用r表示,假设建在(a,b)处最合理
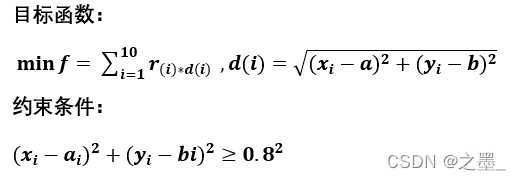
MatLab程序:
目标函数.m:
function f1 = F_x(a)
% 各栋楼房的坐标
x=[0 0.50 0.72 0.77 2.58 2.87 4.43 5.70 6.20 7.76];
y=[0 6.39 0.52 4.94 3.42 5.06 4.76 4.16 3.26 3.96];
r=[700 800 1000 700 1200 900 1300 800 1100 1200];
f1 = 0;
for i =1:10
f1 = f1 + r(i)*sqrt((a(1)-x(i)).^2+(a(2)-y(i)).^2) ;
end
end
约束条件.m:
function [g,h] = limit_Fx(a)
% g为非等式约束
% h为等式约束
% 各栋楼房的坐标
x=[0 0.50 0.72 0.77 2.58 2.87 4.43 5.70 6.20 7.76];
y=[0 6.39 0.52 4.94 3.42 5.06 4.76 4.16 3.26 3.96];
h = [];
g = zeros(1,10);
for i = 1:10
g(i) = -(a(1)-x(i)).^2 -(a(2)-y(i)).^2 +0.64;
end
end
求最优解.m:
clear;clc;close all
% 调用fmincon函数
a = [0,0]; % 最优解迭代的初始值
A = []; b = []; % 线性约束不等式
Aeq = []; beq = []; % 线性约束等式
% lb, ub为自变量的上下界
[x,y] = fmincon(@F_x, a, A, b, Aeq, beq, [], [], @limit_Fx);
运行结果:
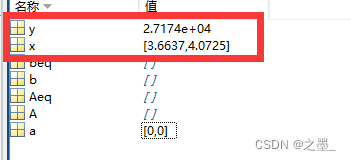
总路程最小值为 (2.717e+04) km
服务中心的地址为:[3.6637,4.0724]
