
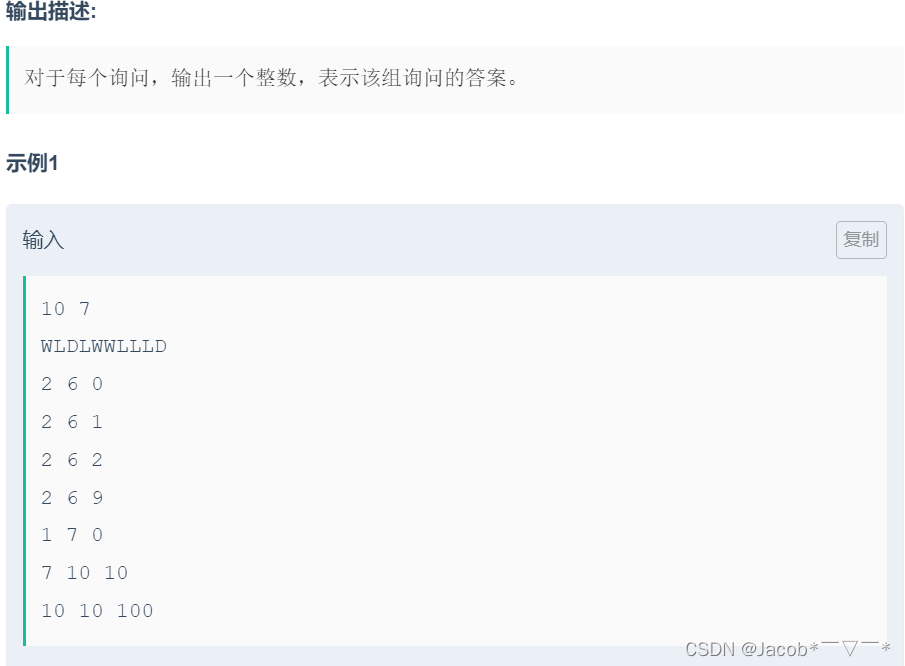

题意:
如题。
思路:
我们注意到 起始分数若在 % 3 意义下相等(即这些起始分值 模 3 结果一致),则 经历 [l, r] 一段后分数的变化量是一个定值(重要)
既然之前有用 ST表 解决过这个问题,那么 线段树 同样可以解决这个问题。
我们可以利用 线段树 这一数据结构维护 [1, n] 整个区间 及其 所有子区间,在不同的模 3 结果之下造成的 分数变化量。
依据题意,本题只需要进行区间修改,因此无需懒标记pushdown操作,只需要pushup操作即可。
设线段树中的 节点为“node”,我们 先应该存储区间的左、右端点:l、r,之后由于要计算 区间分数变化量,且 变化量 与 初始分模 3 的值 有关,因此还需存储一个 大小为 3 的 var 数组。
(当前节点的 var[i] 表示:初始分数 模 3 的结果 为 i ,且经过 当前节点 代表区间 [l, r] 后 的 分数变化量 )。
下方代码设置了一段 节点为 node 的 结构体数组 tr。
struct node
{
int l, r;
ll var[3];
} tr[N<<2];
本题的 关键 显然在于 考虑 pushup 自子向父 更新操作,我们可以和之前一样 分情况讨论:
[l, r] 整段区间 初始值模 3 的结果 为 【i】 的 分数变化量
等于
左半区间 初始值模 3 的结果 为 【i】 的 变化量
加
右半区间 初始值模 3 的结果 为 【(i + 左半区间 初始值模 3 的结果 为 i 的 变化量) % 3】 的 变化量。
代码片段:
void pushup(int u)
{
for(int i=0; i<3; ++i)
{
tr[u].var[i] = tr[u<<1].var[i] + tr[u<<1|1].var[mod3(tr[u<<1].var[i], i)];
}
}
对于线段树中的 每一个叶子结点 中的 var 数组,由于 叶子结点代表的区间长度为 1,我们直接 根据输入的字符串 进行 赋值 即可。
我们先将其存入一个 二维数组 a[3][N] 中,
for(int i=1; i<=n; ++i)
{
char s; scanf("%c", &s);
if(s=='W')
{
a[0][i] = a[1][i] = a[2][i] = 1;
}
else if(s=='L')
{
a[0][i] = 0;
a[1][i] = a[2][i] = -1;
}
else
{
a[0][i] = a[1][i] = a[2][i] = 0;
}
}
之后在 build 函数 中赋值给 叶子结点,回溯时 由 pushup 函数 从叶子结点 向上更新。
void build(int u, int l, int r)
{
tr[u] = {l, r};
if(l==r)
{
for(int i=0; i<3; ++i)
{
tr[u].var[i] = a[i][l];
}
return ;
}
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
pushup(u);
}
对于 ask 查询函数,我们设置其 返回值 为 初始值为 start,其模 3 结果为 rmd = start % 3 且经过 区间 [l, r] 后的 分数变化量,
显然答案即为 start + ask(......)
代码片段:
long long ask(int u, int l, int r, int rmd)//参数 rmd 表示 实时分数 模 3 的结果
{
if(l<=tr[u].l && r>=tr[u].r) return tr[u].var[rmd];
int mid = tr[u].l + tr[u].r >> 1;
long long res = 0;
if(l<=mid) res += ask(u<<1, l, r, mod3(rmd, res));
if(r>=mid+1) res += ask(u<<1|1, l, r, mod3(rmd, res));
return res;
}
至此,本题分析完毕。
如果要学习一下线段树,可以戳这:线段树蓝书讲解 + 经典例题AcWing 1275. 最大数,本题代码的原型就是 基于此模板。
时间复杂度:
O ( n l o g n + q ) O(nlogn + q) O(nlogn+q)(常数比倍增做法大)
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5+10, mod = 3;
int n, q;
ll a[3][N];
struct node
{
int l, r;
ll var[3];
} tr[N<<2];
int mod3(int a, int b)
{
return ((a + b) % mod + mod) % mod;
}
void pushup(int u)
{
for(int i=0; i<3; ++i)
{
tr[u].var[i] = tr[u<<1].var[i] + tr[u<<1|1].var[mod3(tr[u<<1].var[i], i)];
}
}
void build(int u, int l, int r)
{
tr[u] = {l, r};
if(l==r)
{
for(int i=0; i<3; ++i)
{
tr[u].var[i] = a[i][l];
}
return ;
}
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
pushup(u);
}
ll ask(int u, int l, int r, int rmd)//参数 rmd 表示 实时分数 模 3 的结果
{
if(l<=tr[u].l && r>=tr[u].r) return tr[u].var[rmd];
int mid = tr[u].l + tr[u].r >> 1;
ll res = 0;
if(l<=mid) res += ask(u<<1, l, r, mod3(rmd, res));
if(r>=mid+1) res += ask(u<<1|1, l, r, mod3(rmd, res));
return res;
}
int main()
{
cin>>n>>q;
getchar();
for(int i=1; i<=n; ++i)
{
char s; scanf("%c", &s);
if(s=='W')
{
a[0][i] = a[1][i] = a[2][i] = 1;
}
else if(s=='L')
{
a[0][i] = 0;
a[1][i] = a[2][i] = -1;
}
else
{
a[0][i] = a[1][i] = a[2][i] = 0;
}
}
build(1, 1, n);
while(q--)
{
int l, r, start;
scanf("%d%d%d", &l, &r, &start);
printf("%lld\n", start + ask(1, l, r, start % mod));
}
return 0;
}
