- 三维形体投影面积
在 n x n 的网格 grid 中,我们放置了一些与 x,y,z 三轴对齐的 1 x 1 x 1 立方体。
每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。
现在,我们查看这些立方体在 xy 、yz 和 zx 平面上的投影。
投影 就像影子,将 三维 形体映射到一个 二维 平面上。从顶部、前面和侧面看立方体时,我们会看到“影子”。
返回 所有三个投影的总面积 。
示例 1:
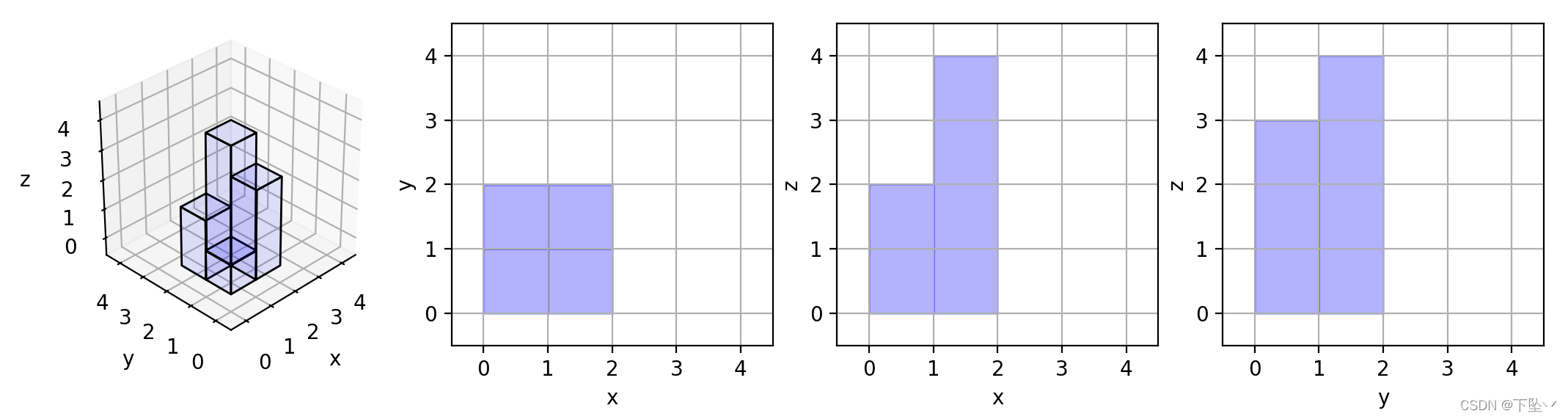
输入:[[1,2],[3,4]]
输出:17
解释:这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。
再水一道简单题吧,这个题感觉最难懂的就是题目了,思路倒是很简单,自己看了一会看懂了,算是记录一下自己提升了下阅读能力吧。对应每个坐标就是有多少方块摞着,比如1在(0,0)2在(0,1)。分别表示(0,0)位置有1个方块,(0,1)位置有两个方块叠着放。那么顶上就很好计算了,只要这个位置有方块,顶上看着就是1,正视图应该是每一列最高的方块的和,侧视图则是每一行中最高的方块的和。
代码思路就很简单了,感觉读题意也好重要,有时候别人都快写完了自己还看不懂题目…
class Solution {
public:
int projectionArea(vector<vector<int>>& grid) {
int n=grid.size();
int m=grid[0].size();
int ans=0;
//侧面,每行最大的
for(int i=0;i<n;i++)
{
int temp=0;
for(int j=0;j<m;j++)
{
if(grid[i][j]!=0)
{
ans+=1;
}
temp=max(grid[i][j],temp);
}
ans+=temp;
}
//正面,每列最大的
for(int i=0;i<m;i++)
{
int temp=0;
for(int j=0;j<n;j++)
{
temp=max(grid[j][i],temp);
}
ans+=temp;
}
return ans;
}
};
