概述
分析
-
两个题目类似,实现的关键在于如何模拟遍历的顺序
-
根据题目要求,遍历的顺序为:从左到右;从下到上;从右到左;从下到上,我们需要模拟该操作;
-
需要注意的是,我们要固定区间取值的规则,即选择左闭右开,还是左闭右闭
-
如果我们使用左闭右开,我们模拟一下示例1,发明正中间的5最后是无法遍历到的
实际上,只要无法完整的循环走完一圈,一定会有一个元素无法遍历到,所以需要额外处理最后可能没有完整一圈的情况
比如说,最后一圈不完整,假设是1 2 3,则3这个元素无法遍历到; 但是,如果最后一圈完整,假设是 1 2 4 5 , 则可以完成遍历1->2->5->4 -
如果我们使用左边右闭,可以解决上面的问题,但是我们就需要限制每次转弯的第一个元素不应该读(因为在前一个方向已经读过了)
1 2 3 4 5 6 7 8 9 123->69->87->45因此,考虑保存每次起始的位置以及终点的位置
-
思路
如何处理方法1的特殊情况?
- 因为只有最后一圈可能是非完整的,所以我们必须在前面完整圈遍历完成后,再格外判断是否有非完整的最后一圈
- 我们可以根据矩阵的边长来判断,只要有奇数边,就说明有非完整的最后一圈
什么时候循环结束?
-
最容易想到的应该是统计遍历的元素个数,当元素个数等于矩阵内方块数就说明循环结束了
-
但是如果我们使用左闭右开区间,则不能这样做,因为总是有一个元素无法遍历
而且,为了处理这个元素,我们需要额外处理最后没有完整一圈的情况,就根无法确定访问的元素个数了
所以,这种情况,需要统计的是矩阵中可以完整的遍历圈数
-
如果使用左闭右开,因为可以确保每个元素都能访问到,所以可以直接统计遍历的元素的个数
代码
54
方法1:
-
分析左闭右开的遍历过程中的循环遍历,假设行循环遍历是row,列循环遍历是column
1 2 3 4 5 6 7 8因为是左闭右开,当从左到右遍历结束时,row,column的值都是合法的,且正好也是要遍历的列的起始位置,于是可以直接进行下一个遍历
这也是我最开始考虑这种方法的原因
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> res;
int m = matrix.size() , n = matrix[0].size();
int Loop = min(m, n) / 2; // 不保证一定是个正方形,要根据最小的边确定可以完整遍历圈数
int row = 0, column = 0;
int offset = 0;
while(Loop--){
// 从左到右
for(; column < n - 1 - offset; ++column) // 左闭右开,所以右边界限需要多减1
res.push_back(matrix[row][column]);
// 从上到下
for(; row < m - 1 - offset; ++row)
res.push_back(matrix[row][column]);
// 从右往左
for(; column > 0 + offset; --column) // 左闭右开,所以右边界限>0而不是等于0
res.push_back(matrix[row][column]);
for(; row > 0 + offset; --row)
res.push_back(matrix[row][column]);
++row; // 下一个起始位置
++column;
++offset; // 因为已经循环了一圈,所以下一圈的边界需要改变
}
// 额外处理
if (min(m, n) % 2 == 1) { //当较小的一维为奇数时,最内层会剩下一行或者一列。
if (m <= n) {
for (; column <= n - 1 - offset; ++column) {
res.push_back(matrix[row][column]);
}
} else {
for (; row <= m - 1 - offset; ++row) {
res.push_back(matrix[row][column]);
}
}
}
return res;
}
};
方法2:
-
分析左闭右开的遍历过程中的循环遍历,假设行循环遍历是row,列循环遍历是column
1 2 3 4 5 6 7 8因为是左闭右闭,当从左到右遍历结束时,row,column的值都是不合法的(这里的情况是row=0,colomn = 4),如果继续用两个循环遍历的话,那么在每次遍历后都需要改变这两个值
比较麻烦,而且经过测试,无法通过该题
1 2 3 4 5 6 7 8 1 1 1 1前面一圈都没问题,第二圈从row=1 column=1开始,等到第一次遍历到(1,2)时,下一次遍历不进行,但是也会改变row,column的值,导致错误
-
我们知到,最重要的就是确定遍历的界限,于是,可以考虑用四个遍历来确定每次遍历的界限
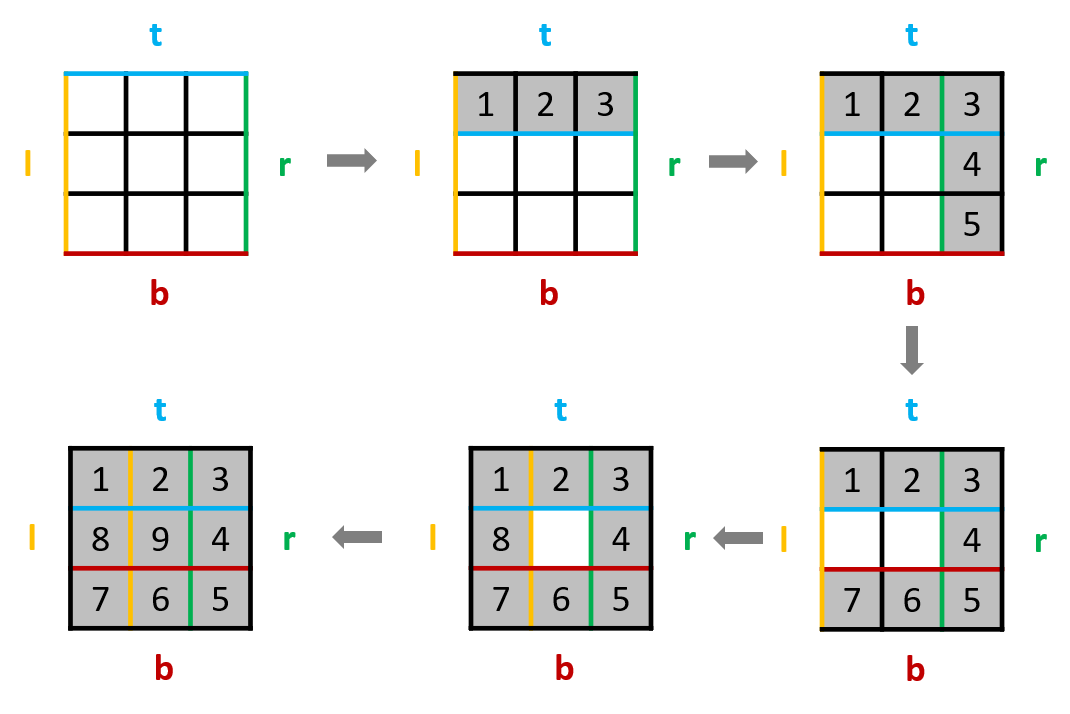
l,r,t,b分别记录区间的范围
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix){
int num = 1;
int m = matrix.size(), n = matrix[0].size();
int left = 0, top = 0, right = n - 1, bottom = m - 1;
//初始化数组
vector<int> res;
while (left <= right && top <= bottom) {
//left to right
for (int i = left; i <= right; ++i) res.push_back(matrix[top][i]);
++top; // 改变从上到下遍历的起始位置
//top to bottom
for (int i = top; i <= bottom; ++i) res.push_back(matrix[i][right]);
--right; // 改变从右到左遍历的起始位置
//right to left
for (int i = right; i >= left && bottom >= top; --i) res.push_back(matrix[bottom][i]);
--bottom; // 改变从下到上遍历的起始位置
//bottom to top
for (int i = bottom; i >= top && right >= left; --i) res.push_back(matrix[i][left]);
++left; // 改变从左到右遍历的起始位置
}
return res;
}
};
59
对于59,只要根据54,修改一下每次循环的操作即可
实际上,因为59限定了是正方形,对方法1的额外处理根方便
方法1
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n));
int row = 0, column = 0;
int count = 1;
int circle_num = 0;
int loop = n / 2;
while(loop--) {
for(; column < n - 1 - circle_num; column++)
res[row][column] = count++;
// cout<<row<<" "<<column<<endl;
for(; row < n - 1 - circle_num; row++)
res[row][column ] = count++;
// cout<<row<<" "<<column<<endl;
for(; column > 0 + circle_num; column--)
res[row][column] = count++;
// cout<<row<<" "<<column<<endl;
for(; row > 0 + circle_num; row--)
res[row][column] = count++;
// cout<<row<<" "<<column<<endl;
// 改变每圈的起始位置
row++;
column++;
// 每圈要缩小1个数字
circle_num++;
}
if(n % 2) // 这里最中间的要单独拿出来
res[row][column] = n*n;
return res;
}
};
方法2
略
