本文首发于馆主君晓的博客,链接:【04-26】力扣每日一题
题目描述
??题目链接在此,883. 三维形体投影面积,题目截图如下:
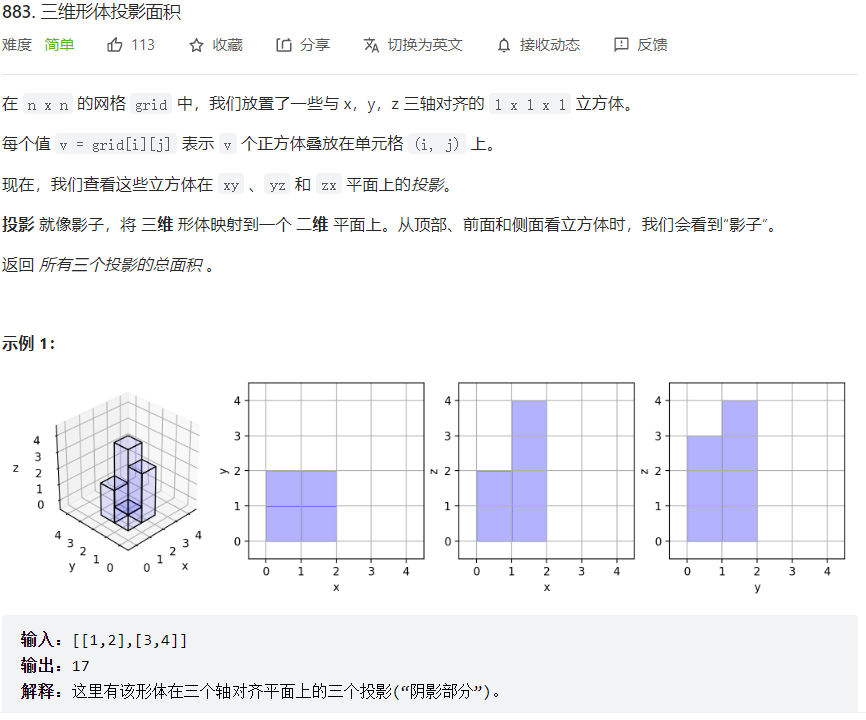
??这道题通俗来说就是从正视图、侧视图、俯视图来数一数一共有多少个正方体。需要注意的是,俯视图中,如果有个方格没有正方体,那是不算的。比如题目中给的例子,正视图有7个,侧视图有6个,俯视图有4个,所以一共17个。
题目分析
??通过上面的题目描述,我们大概知道我们需要干什么了,就是数二维数组中,非零元素的个数,作为我们俯视图的结果。然后每一列最大值之和作为我们正视图的结果。最后每一行最大值之和作为我们侧视图的结果。
代码实现
??考虑到这个二维数据行和列是相同的,所以我们放在一个循环搞定,代码如下:
class Solution {
public:
int projectionArea(vector<vector<int>>& grid) {
int rows = grid.size(),cols= grid.size();
int count = 0,side = 0,front = 0;
for(int i = 0;i<rows;i++){
int tmp_side=0,tmp_front = 0;
for(int j = 0;j<cols;j++){
if(grid[i][j]!=0){
count++;
}
if(grid[i][j]>tmp_side){
// 从行来看
tmp_side = grid[i][j];
}
if(grid[j][i]>tmp_front){
// 从列来看
tmp_front = grid[j][i];
}
}
side+=tmp_side;
front+=tmp_front;
}
return side+front+count;
}
};
结语
??积少成多,积水成渊!水滴石穿,非一日之功!
