文章目录
- 在本文章中, 将会阐述二叉树的三种遍历方式的递归和迭代写法;
- 之前我们写过: tag二叉树-刷题预备知识-1. 深入浅出深度优先遍历(DFS)和广度优先遍历(BFS), 建议反复阅读几遍, 你会懂得,
- 递归和深度优先遍历, 队列/栈和广度优先遍历几乎就是相辅相成的, 而且在你熟练掌握了DFS和BFS之后, 对于这种遍历的题目其实就能够信手拈来了;
- 可能会有些朋友对二叉树的迭代比较发怵, 先学学上文的BFS!
lt.144. 二叉树的前序遍历
[案例需求]
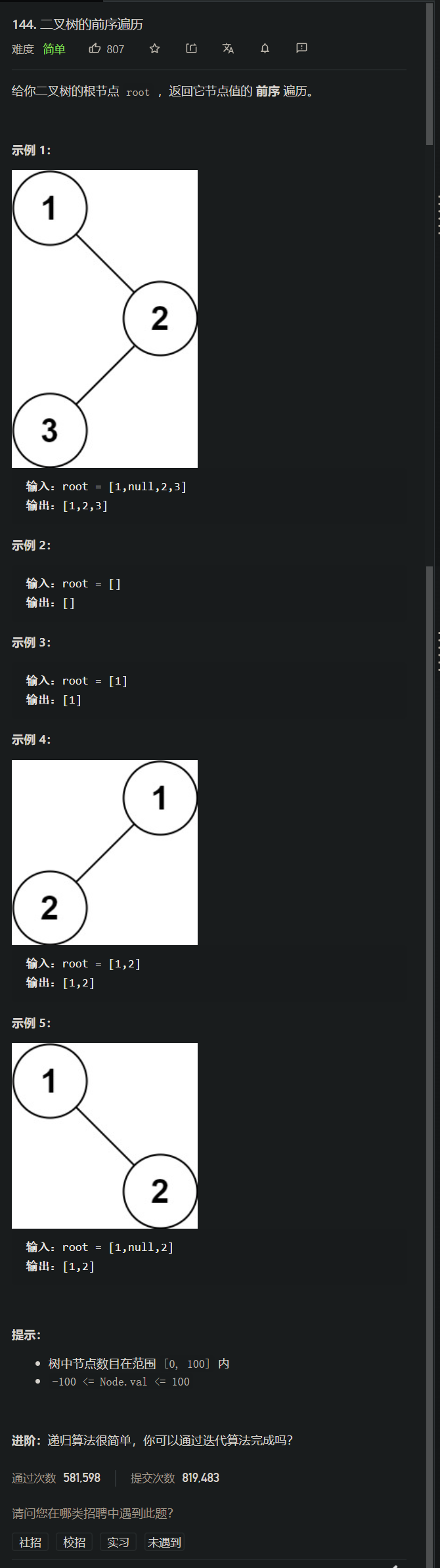
1. 前序遍历的递归法实现
[思路分析一, 递归解法]
[代码实现]
//1. 前序遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
preOrder(root, list);
return list;
}
public void preOrder(TreeNode root, List<Integer> list){
//递归结束
if(root == null)return;
//单层递归的逻辑
list.add(root.val);
//找返回值
preOrder(root.left, list);
preOrder(root.right, list);
}
}
2. 前序遍历的迭代法实现
[思路分析二, 迭代解法]
- 上面的BFS和DFS你看了吗?

- 对于BFS遍历, 我们通常使用队列去实现, 因为BFS是按照每一层进行遍历的, 在添加遍历结点到队列时, 我们会把这个节点的子节点,
先放入到队列缓存, 在遍历完某一层A的结点之后, 下一层B的所有元素也就已经在队列里等着我们啦 - 因为是队列的原因, 所以下一层B的结点顺序和我们此时从队列中取元素的顺序是一致的! 所以在本道题中我们就需要变通一下啦,
- 看上图BFS的动图, 可以看出, 当我们使用队列存取元素时, 对二叉树的遍历是层次遍历, 不符合前序遍历的需求, 问题就差在我们用的是队列存入元素, 如果我们把队列改为栈, 同时颠倒一下存入栈的左右子树的位置, 就是对二叉树的前序遍历啦!
由于“中左右”的访问顺序正好符合根结点寻找子节点的顺序,因此每次循环时弹栈,输出此弹栈结点并将其右结点和左结点按照叙述顺序依次入栈。至于为什么要右结点先入栈,是因为栈后进先出的特性。右结点先入栈,就会后输出右结点。

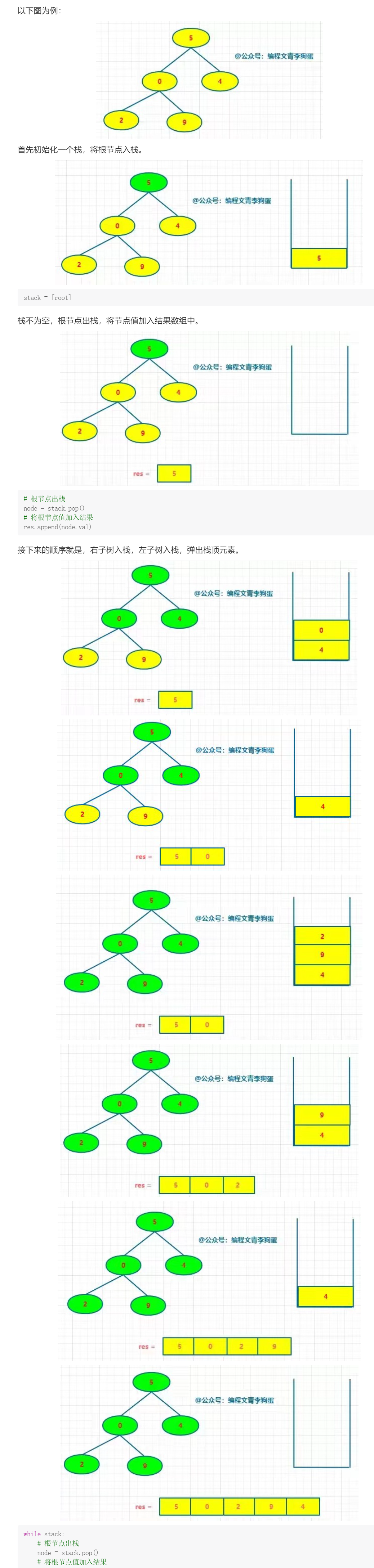
[代码实现]
你可以去前面提到的DFS文章中去比较一下, 是不是特别像! 一通百通!
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
//前序遍历, 迭代法
List<Integer> list = new ArrayList<>();
//特判
if(root == null) return list;
//相比于BFS标准实现, 我们应该用栈存入结点
Stack<TreeNode> st = new Stack<>();
st.push(root);
while(! st.isEmpty()){
root = st.pop();
list.add(root.val);
//注意, 由于栈的特性(先进后出), 为了实现前序遍历, 我们应该先添加右子树结点,再添加左子树结点
if(root.right != null) st.push(root.right);
if(root.left != null) st.push(root.left);
}
return list;
}
}
lt.94. 二叉树的中序遍历
[案例需求]
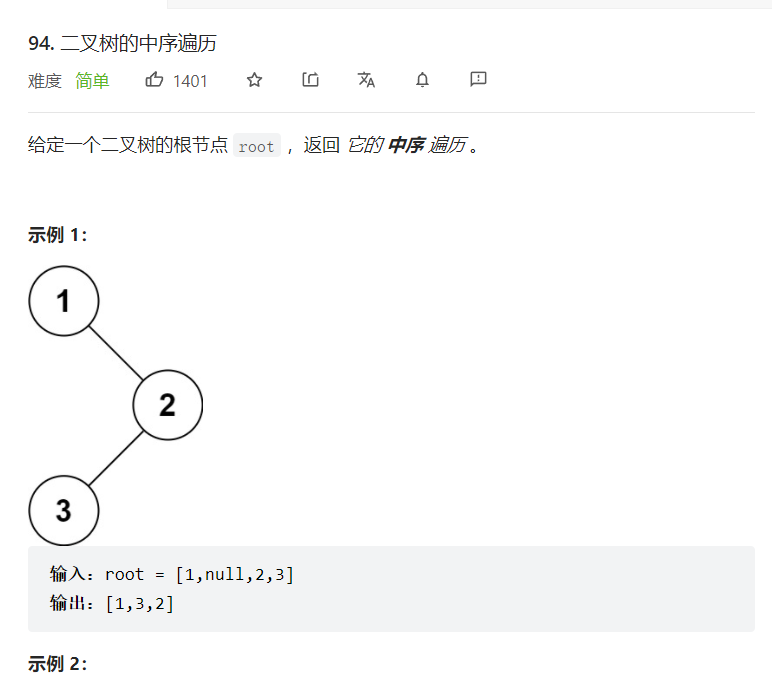
1. 中序遍历的递归法实现
[思路分析一, 递归解法]
[代码实现]
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
inOrder(root, list);
return list;
}
public void inOrder(TreeNode root, List<Integer> list){
//递归终止条件
if(root == null)return;
//单层递归逻辑
inOrder(root.left, list); //不断的递进, 即root的left的left的left
list.add(root.val); //上面的递进结束了, 在这个方法下面是归来过程, list开始存入归来时遇到的所有结点的值
inOrder(root.right, list); // 上面的左子树存完了, 继续往右子树进行递进, 注意哦 由于list.add在这个递归调用的上面, 所以list和这个inorder是一起递进的, 也就是这个inorder和list.add同时进行;
}
}
2. 中序遍历的迭代法实现
[思路分析二, 迭代解法]

[代码实现]
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
//BFS
//递归的调用过程是不断往左边走,当左边走不下去了,就打印节点,并转向右边,然后右边继续这个过程
List<Integer> list = new ArrayList<>();
Stack<TreeNode> st = new Stack<>();
while(!st.isEmpty() || root != null){
//一直向左遍历并存储遇到的结点
while(root != null){
st.push(root);
root = root.left;
}
//走到左边的最下边了
root = st.pop();
list.add(root.val);
root = root.right;
}
return list;
}
}
lt.145. 二叉树的后序遍历
[案例需求]
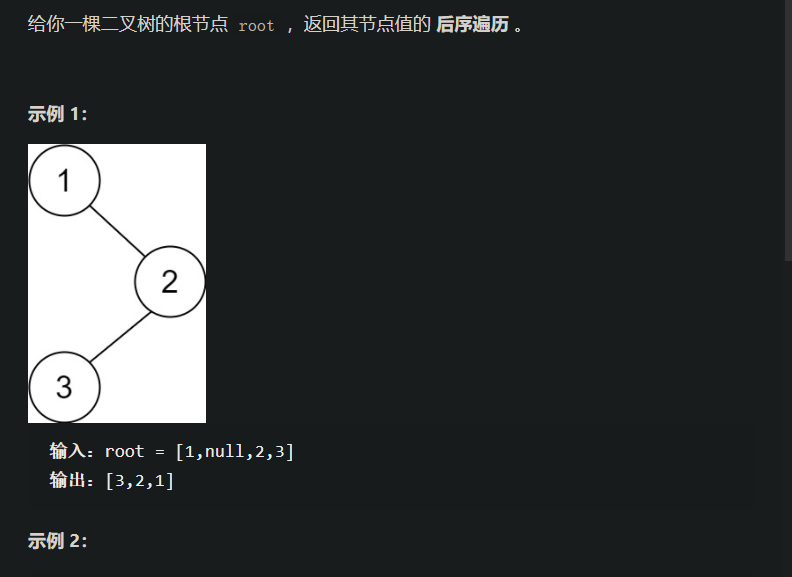
1. 后序遍历的递归法实现
[思路分析一, 递归实现]
- lue
[代码实现]
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
postOrder(root, list);
return list;
}
public void postOrder(TreeNode root, List<Integer> list){
//递归终止条件
if(root == null)return;
//
postOrder(root.left, list);
postOrder(root.right, list);
//单层递归逻辑
list.add(root.val);
}
}

2. 后序遍历的迭代法实现
[思路分析二, 迭代法]
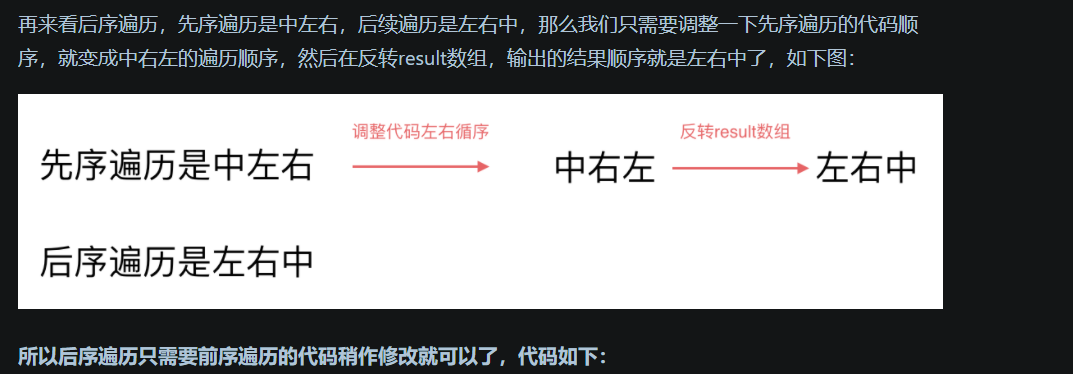
[代码示例]
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
//bfs
List<Integer> list = new ArrayList<>();
Stack<TreeNode> st = new Stack<>();
if(root == null) return list;
st.push(root);
while(! st.isEmpty()){
root = st.pop();
list.add(root.val);
if(root.left != null)st.push(root.left);
if(root.right != null)st.push(root.right);
}
Collections.reverse(list);
return list;
}
}


