总结
涉及到的知识点为二分、计算几何、树上启发式合并、二分图最小边染色。
二分时要注意未找到时需要特判。计算几何被卡精度时要能想到哪里可能被卡。树上启发式合并是一种优秀的dfs序莫队替代品,适用于无修改的子树相关问题。学会了二分图最小边染色。
A - Extract Numbers
题意
给定长度为 1 0 5 10 ^ 5 105 的字符串,逗号和分号将其分为若干字串,判断每个字串是否为整数的形式。
思路
模拟,复杂度 O ( n ) O(n) O(n) 。
代码
import re
str = input()
lst = re.split('[,;]', str)
ans1 = []
ans2 = []
for s in lst:
if s.isdigit() and (s == '0' or s[0] != '0'):
ans1.append(s)
else:
ans2.append(s)
if len(ans1) == 0:
print('-')
else:
print('"' + ','.join(ans1) + '"')
if len(ans2) == 0:
print('-')
else:
print('"' + ','.join(ans2) + '"')
B - Queries about less or equal elements
题意
给定两个长度为 2 × 1 0 5 2 \times 10^5 2×105 的整形序列 a a a, b b b,对 b b b 中每一个元素 b i b_i bi? 求 a a a 中有多少个元素不大于 b i b_i bi? 。
思路
将 a a a 排序后,二分找到最后一个小于等于 b i b_i bi? 的点,如果找到的点的坐标为 0 0 0 ,答案可能是 0 0 0 或 1 1 1,需要再check一下。复杂度 O ( m ? n log ? n ) O(m \cdot n \log n) O(m?nlogn) 。
代码
#include <bits/stdc++.h>
using namespace std;
signed main() {
ios::sync_with_stdio(false);
cin.tie(0);
int n, m; cin >> n >> m;
vector<int> a(n), b(m);
for(int i = 0; i<n; i++) cin >> a[i];
for(int i = 0; i<m; i++) cin >> b[i];
sort(a.begin(), a.end());
for(int i = 0; i<m; i++) {
int x = b[i];
int l = 0, r = n - 1;
while(l < r) {
int mid = (l + r + 1) >> 1;
if(a[mid] <= x) l = mid;
else r = mid - 1;
}
if(l == 0 && a[0] > x) cout << "0" << " ";
else cout << l+1 << " ";
}
return 0;
}
C - Make Palindrome
题意
给定长度为 2 × 1 0 5 2 \times 10^5 2×105 的字符串,可以使用 1 1 1 代价将其中一个字符转化为任意字符,可以使用 0 0 0 代价将这个字符串重新排列。求在代价最小的情况下可以变成的字典序最小的回文串。
思路
对于任意一个字符串,我们统计每个字符出现的次数,只有所有字符出现次数均为偶数或仅一种字符出现次数为奇数时,这个字符串才能被重新排列成回文串。
如果题目给出的字符串恰好符合上面的情况,直接重新排列后输出即可。给定的字符串不满足上述条件时,我们选择两种出现次数为奇数的字符,取出其中一种字符中的一个,使用 1 1 1 代价将其转换为另一种字符,这样就会减少两种出现次数为奇数的字符,不断进行上述操作就可以使字符串满足上述条件。
当每次进行转换时,我们选择 ASCII 码最大的字符转化为 ASCII 码最小的,这样转化是最优的。
考虑将字符串重新排序这一步骤,如果字符串中存在出现次数为奇数的字符,那么必须要将一个这种字符放在答案的正中间,这样以后所有字符出现次数均为偶数。我们将每种字符分成两等份,各一份放在前半部分升序,各一份放在后半部分降序。
复杂度 O ( n ? log ? 26 ) O(n \cdot \log 26) O(n?log26) 。
代码
#include <bits/stdc++.h>
using namespace std;
signed main() {
ios::sync_with_stdio(false);
cin.tie(0);
string s; cin >> s;
// 统计每种字符出现的次数
map<char, int> mp;
for(int i = 0; i<s.size(); i++) {
mp[s[i]]++;
}
// 找到所有出现次数为奇数的字符
vector<char> odd_v;
for(auto p : mp) {
if(p.second & 1) odd_v.push_back(p.first);
}
// 选取最大的字符转换为最小的
for(int i = 0; i<odd_v.size()/2; i++) {
char a = odd_v[i], b = odd_v[odd_v.size() - i - 1];
mp[a]+=1;
mp[b]-=1;
}
// 生成答案
string pa, pb;
for(auto p : mp) {
int cnt = p.second;
for(int i = 0; i<cnt/2; i++) pa.push_back(p.first);
}
// 取出最中间的奇数字符放在答案的最中间
if(odd_v.size() & 1) pb += odd_v[odd_v.size()/2];
string ans = pa+pb;
reverse(pa.begin(), pa.end());
ans += pa;
cout << ans << endl;
return 0;
}
D - Area of Two Circles’ Intersection
题意
求两圆的面积交。
思路
模板题,但板子被卡精度了,改一改才能过去。
对于外切、相离、内含、内切的情况特判并返回。只需要考虑相交的情况。
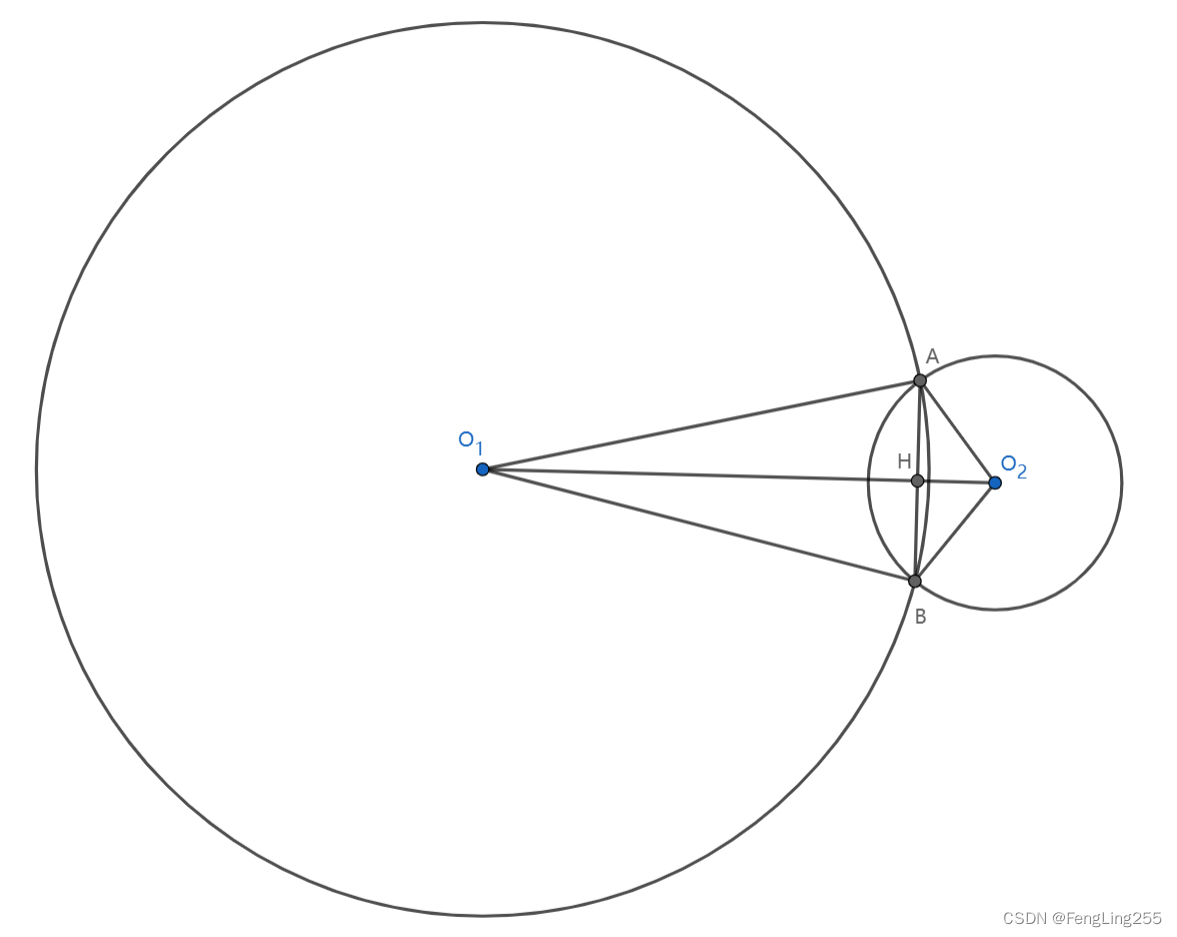
参照上图,推一下式子。
在 △ A O 1 O 2 \triangle AO_1O_2 △AO1?O2? 中,根据余弦定理得 ∣ O 1 A ∣ 2 + ∣ O 1 O 2 ∣ 2 ? ∣ A O 2 ∣ 2 = 2 ? ∣ O 1 A ∣ ? ∣ O 1 O 2 ∣ ? cos ? ∠ A O 1 O 2 {\vert O_1A \vert}^2 + {\vert O_1O_2 \vert}^2 - {\vert AO_2 \vert}^2 = 2 \cdot {\vert O_1A \vert} \cdot {\vert O_1O_2 \vert} \cdot \cos\angle{AO_1O_2} ∣O1?A∣2+∣O1?O2?∣2?∣AO2?∣2=2?∣O1?A∣?∣O1?O2?∣?cos∠AO1?O2?
得到 ∣ O 1 H ∣ = ∣ O 1 A ∣ ? cos ? ∠ A O 1 O 2 ? ∣ O 1 A ∣ 2 + ∣ O 1 O 2 ∣ 2 ? ∣ A O 2 ∣ 2 2 ? ∣ O 1 O 2 ∣ \vert O_1H \vert = \vert O_1A \vert \cdot \cos\angle{AO_1O_2} \cdot \frac{{\vert O_1A \vert}^2 + {\vert O_1O_2 \vert}^2 - {\vert AO_2 \vert}^2}{ 2 \cdot {\vert O_1O_2 \vert}} ∣O1?H∣=∣O1?A∣?cos∠AO1?O2??2?∣O1?O2?∣∣O1?A∣2+∣O1?O2?∣2?∣AO2?∣2?
∠ A O 1 O 2 = arccos ? ∣ O 1 H ∣ ∣ O 1 A ∣ \angle {AO_1O_2} = \arccos \frac{\vert O_1H \vert}{\vert O_1A \vert} ∠AO1?O2?=arccos∣O1?A∣∣O1?H∣?
∠ A O 2 O 1 = arccos ? ∣ O 1 O 2 ∣ ? ∣ O 1 H ∣ ∣ O 1 A ∣ \angle {AO_2O_1} = \arccos \frac{\vert O_1O_2 \vert - \vert O_1H \vert}{\vert O_1A \vert} ∠AO2?O1?=arccos∣O1?A∣∣O1?O2?∣?∣O1?H∣?
扇形 O 1 A B O_1AB O1?AB 的面积 a r e a 1 = ∣ O 1 A ∣ 2 ? ∠ A O 1 O 2 area_1 = {\vert O_1A \vert}^2 \cdot \angle{AO_1O_2} area1?=∣O1?A∣2?∠AO1?O2?
扇形 O 2 A B O_2AB O2?AB 的面积 a r e a 2 = ∣ O 2 A ∣ 2 ? ∠ A O 2 O 1 area_2 = {\vert O_2A \vert}^2 \cdot \angle{AO_2O_1} area2?=∣O2?A∣2?∠AO2?O1?
多边形 A O 1 B O 2 AO_1BO_2 AO1?BO2? 的面积 a r e a 3 = ∣ O 1 A ∣ ? ∣ O 1 O 2 ∣ ? sin ? ∠ A O 1 O 2 area_3 = \vert O_1A \vert \cdot \vert O_1O_2 \vert \cdot \sin{\angle{AO_1O_2}} area3?=∣O1?A∣?∣O1?O2?∣?sin∠AO1?O2?
答案为 a r e a 1 + a r e a 2 ? a r e a 3 area_1 + area_2 - area_3 area1?+area2??area3?
因为精度问题,多边形面积公式应该改为 a r e a 3 = 1 2 ∣ O 1 A ∣ ∣ O 1 B ∣ sin ? ∠ A O 1 B + 1 2 ∣ O 2 A ∣ ∣ O 2 B ∣ sin ? ∠ A O 2 B area_3 = \frac{1}{2} \vert O_1A \vert \vert O_1B \vert \sin\angle{AO_1B} + \frac{1}{2} \vert O_2A \vert \vert O_2B \vert \sin\angle{AO_2B} area3?=21?∣O1?A∣∣O1?B∣sin∠AO1?B+21?∣O2?A∣∣O2?B∣sin∠AO2?B
代码
#include <bits/stdc++.h>
using namespace std;
#define double long double
const double eps = 1e-18;
const double pi = acos(-1.0);
int sign(double x) {
if(fabs(x) < eps) return 0;
return x < 0 ? -1 : 1;
}
int cmp(double x, double y) {
return sign(x - y);
}
const double squ(double x) {return x*x; }
struct Point{
double x, y;
};
using Vector = Point;
Vector operator + (Vector a, Vector b) { return Vector{a.x + b.x, a.y + b.y}; }
Vector operator - (Vector a, Vector b) { return Vector{a.x - b.x, a.y - b.y}; }
Vector operator * (Vector a, double p) { return Vector{a.x * p, a.y * p}; }
Vector operator / (Vector a, double p) { return Vector{a.x / p, a.y / p}; }
double dot(Vector a, Vector b) {
return a.x * b.x + a.y * b.y;
}
double get_length(Vector a) {
return sqrt(dot(a, a));
}
double get_angle(Vector a, Vector b) {
return acos(dot(a, b) / get_length(a) / get_length(b));
}
struct Circle {
Point o; double r;
};
double circle_circle_intersection_area(const Circle &c1, const Circle &c2) {
double d = get_length((c1.o - c2.o));
if (sign(d - (c1.r + c2.r)) >= 0) return 0;
if (sign(d - abs(c1.r - c2.r)) <= 0) {
double r = min(c1.r, c2.r);
return r * r * pi;
}
double x = (d * d + c1.r * c1.r - c2.r * c2.r) / (2.0 * d),
t1 = acos(x / c1.r), t2 = acos((d - x) / c2.r);
return c1.r * c1.r * t1 + c2.r * c2.r * t2 - (c1.r * c1.r * sinl(t1 * 2) + c2.r * c2.r * sinl(t2 * 2)) / 2.0;
// return c1.r * c1.r * t1 + c2.r * c2.r * t2 - d * c1.r * sin(t1); // d和c1.r过大而t1过小会被卡
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0);
Circle a, b;
cin >> a.o.x >> a.o.y >> a.r;
cin >> b.o.x >> b.o.y >> b.r;
cout << fixed << setprecision(30) << circle_circle_intersection_area(a, b);
return 0;
}
E - Lomsat gelral
题意
给一棵含有 n n n ( n ≤ 1 0 5 ) (n \leq 10^5) (n≤105) 个结点的树,每一个结点 i i i 有一种颜色 c i c_i ci? ( 1 ≤ c i ≤ n ) (1 \leq c_i \leq n) (1≤ci?≤n) ,对于每一个结点,求出其子树出现次数最多的颜色的颜色和。
思路
树上启发式合并(dsu on tree)的模板题目。推荐学习视频 【AgOHの算法胡扯】树上启发式合并(dsu on tree)
首先要知道轻重儿子的概念。对于一个结点的多个儿子,所在子树结点最多的儿子成为重儿子,其余儿子均称为轻儿子。可以先使用一遍dfs处理出所有结点的重儿子。
接下来再进行一遍dfs求出答案。这次dfs过程中,一边搜索,我们要一边维护一个数组cnt代表搜索到当前状态时,每种颜色出现的次数。dfs进行到当前结点
u
u
u 时,我们要先递归地搜索
u
u
u 的所有轻儿子,递归地将轻儿子的答案统计完毕。接下来搜索一遍
u
u
u 的重儿子,再使用count函数统计当前结点
u
u
u 的答案。
需要注意的是,对于当前结点
u
u
u ,搜索完每一个轻儿子,都需要把这个轻儿子的贡献删除掉。这样做是为了防止在连续搜索两个轻儿子时,第一个对cnt造成的影响干扰到第二个轻儿子答案的计算。
还需要注意的是,count函数内部暴力搜索了所有轻儿子。看起来复杂度虽然是
O
(
n
2
)
O(n^2)
O(n2) 的,但是我们执行的暴力统计都是对轻边连接的子树,因此每个点被遍历到的次数和它一直向上到根的轻边数有关,而轻边数不会超过
log
?
n
\log n
logn ,所以算法的复杂度其实是
O
(
n
log
?
n
)
O(n \log n)
O(nlogn) 的。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+20;
const int maxm = 2e5+20;
int h[maxn], e[maxm], ne[maxm], top;
void add(int a, int b) {
e[top] = b, ne[top] = h[a], h[a] = top++;
}
int n;
int sz[maxn], son[maxn]; // 每个结点子树的大小,每个结点的重儿子
void dfs(int u, int fa) {
sz[u] = 1;
for(int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if(v == fa) continue;
dfs(v, u);
sz[u] += sz[v];
if(sz[v] > sz[son[u]])
son[u] = v;
}
}
int color[maxn]; // 每个点的颜色
int cnt[maxn]; // dfs过程中每种颜色出现的次数
long long ans[maxn], sum;
int flag, maxc;
// 暴力统计结点u的所有轻儿子对cnt的影响
void count(int u, int fa, int val) {
cnt[color[u]] += val;
if(cnt[color[u]] > maxc) {
maxc = cnt[color[u]];
sum = color[u];
} else if(cnt[color[u]] == maxc) {
sum += color[u];
}
for(int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if(v == fa || v == flag) continue;
count(v, u, val);
}
}
// keep为是否保留影响,若节点是轻儿子则不保留,若结点是重儿子,则保留
void dfs(int u, int fa, bool keep) {
// 搜索轻儿子,并删除影响
for(int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if(v == fa || v == son[u]) continue;
dfs(v, u, false);
}
// 搜索重儿子,保留影响
if(son[u]) {
dfs(son[u], u, true);
flag = son[u]; // 记录一下当前结点的重儿子,下面count函数内会用到
}
//暴力搜索轻儿子计算答案
count(u, fa, 1);
flag = 0;
ans[u] = sum;
// 如果当前结点是父亲的轻儿子,则删除自身的影响
if(!keep) {
count(u, fa, -1);
sum = maxc = 0;
}
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
memset(h, -1, sizeof h);
cin >> n;
for(int i = 1; i<=n; i++) cin >> color[i];
for(int i = 1; i<n; i++) {
int a, b; cin >> a >> b;
add(a, b); add(b, a);
}
dfs(1, 0); // 第一遍dfs处理出每个结点的重儿子
dfs(1, 0, 0); // 计算答案
for(int i = 1; i<=n; i++) cout << ans[i] << " ";
return 0;
}
F - Edge coloring of bipartite graph
题意
给定点数 1000 1000 1000 边数 1 0 5 10^5 105 的 二分图,求最小边染色(给每一条边染一个颜色,有公共点的边颜色不能相同,求至少需要多少种颜色)。
思路
有一个结论:二分图的最小边染色为点的最大度数。
枚举所有边,对于每一条边的起点 s s s 和终点 t t t ,分别找到它们最小的可选颜色 c 1 , c 2 c1, c2 c1,c2,如果 c 1 = c 2 c1 = c2 c1=c2 ,直接将这条边染成这个颜色;否则。需要将其中的一个点的连边方式进行调整再染色。
调整方式如下。 c 1 ≠ c 2 c1 \neq c2 c1?=c2 时,如果 c 2 < c 1 c2 \lt c1 c2<c1 ,那么直接将这条边染色成 c 1 c1 c1 是合法方案,我们就直接这样做;如果 c 2 > c 1 c2 \gt c1 c2>c1 ,说明点 t t t 已经存在一条邻边被染成了 c 1 c1 c1,我们先强行将当前边染色成 c 1 c1 c1,再将与其产生冲突的边调整为 c 2 c2 c2,如果这次调整又产生了新的冲突,则按照同样的方式调整新的冲突。
复杂度 O ( n × m ) O(n \times m) O(n×m)
代码
#include <bits/stdc++.h>
using namespace std;
int n1, n2, m;
const int maxn = 2050;
const int maxm = 1e5+20;
struct Edge {
int x, y;
} edges[maxm];
int to[maxn][maxn];
int de[maxn];
signed main() {
ios::sync_with_stdio(false);
cin.tie(0);
int ans = 0;
cin >> n1 >> n2 >> m;
for(int i = 0; i<m; i++) {
int x, y; cin >> x >> y; y += 1000;
edges[i] = {x, y};
de[x]++, de[y]++;
ans = max({ans, de[x], de[y]});
}
for(int i = 0; i<m; i++) {
int c1 = 1, c2 = 1;
Edge& e = edges[i];
while(to[e.x][c1]) c1++;
while(to[e.y][c2]) c2++;
to[e.x][c1] = e.y;
to[e.y][c2] = e.x;
if(c1 != c2)
for(int now = e.y, c = c2; now; now = to[now][c], c ^= c1 ^ c2)
swap(to[now][c1], to[now][c2]);
}
cout << ans << "\n";
for(int i = 0; i<m; i++) {
Edge& e = edges[i];
int color = 0;
while(to[e.x][color] != e.y) color++;
cout << color << " ";
}
return 0;
}
