1. 逆序数
解释:在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。
举例:
序列:2 4 3 1
2,4
2,3
2,1 ==> 一个逆序( 因为2比1大,但是2却排在了1的前面,那么这就是一个逆序)
4,3 ==> 一个逆序( 因为4比3大,但是4却排在了3的前面,那么这就是一个逆序)
4,1 ==> 一个逆序( 因为4比1大,但是4却排在了1的前面,那么这就是一个逆序)
3,1 ==> 一个逆序( 因为3比1大,但是3却排在了1的前面,那么这就是一个逆序)
2. 问题描述
给定一个正整数序列,求出其逆序数。
3. 输入格式
第一行,一个数 n,表示序列中有 n 个数。
第二行 n 个数,表示给定的序列。序列中每个数字不超过 109。
4. 输出格式
输出序列中逆序对的数目。
5. 输入输出示例
输入:
6
5 4 2 6 3 1
输出:
11
6. 解决思路
- 利用归并排序的方法,在比较左右子序列大小的同时,如果左序列值大于右序列值,那么就是一个逆序,记录到结果。
- 要注意的是,这时左序列中比当前左序列值大的值都会和当前右序列值构成逆序。
- 其余操作同归并排序,最终将序列变成有序序列。
7. 代码示例
typedef struct{
int num_1;
int num_2;
}Npair;
vector<Npair> v;
void mergesort(int* a,int b,int e){//归并排序 参数:数组名 首位下标 末位下标
if(b==e)
return;
int mid=(b+e)>>1,i=b,j=mid+1,k=b;
int* c = (int*)malloc((e-b+1)*sizeof(int));
mergesort(a,b,mid),mergesort(a,mid+1,e);
while(i<=mid&&j<=e)
if(a[i]<=a[j])
c[k++]=a[i++];
else{
/************核心代码块************/
/************核心代码块************/
for(int m = i;m<=mid;++m){
Npair npair;
npair.num_1 = a[m];
npair.num_2 = a[j];
v.push_back(npair);
}
/************核心代码块************/
/************核心代码块************/
c[k++]=a[j++];//统计答案
}
while(i<=mid)
c[k++]=a[i++];
while(j<=e)
c[k++]=a[j++];
for(int l=b;l<=e;l++)
a[l]=c[l];
}
/*
*主函数
*/
int main(){
int n;
cin>>n;
int a[n];
for(int i=0;i<n;++i)cin>>a[i];
cout<<endl<<"初始序列为:";
for(int i = 0;i<6;++i)
cout<<a[i]<<" ";
cout<<endl<<endl;
mergesort(a,0,5); //参数:数组名 首位下标 末位下标
cout<<"排序后序列:";
for(int i = 0;i<6;++i)
cout<<a[i]<<" ";
cout<<endl<<endl;
cout<<"逆序对:";
for(vector<Npair>::iterator it = v.begin();it!=v.end();it++)
cout<<'['<<(*it).num_1<<','<<(*it).num_2<<']'<<" ";
cout<<endl<<endl;
cout<<"逆序数:"<<v.size()<<endl;
return 0;
}
8. 运行结果
6
5 4 2 6 3 1
初始序列为:5 4 2 6 3 1
排序后序列:1 2 3 4 5 6
逆序对:[5,4] [4,2] [5,2] [6,3] [3,1] [6,1] [2,1] [4,1] [5,1] [4,3] [5,3]
逆序数:11
Process returned 0 (0x0) execution time : 8.335 s
Press any key to continue.
9. 归并排序
-
定义: 归并排序是建立在归并操作上的一种有效的排序算法,采用的方法是分治二分。
-
时间复杂度:
O(n log n) -
空间复杂度:
O(n) -
自底向上的归并排序:
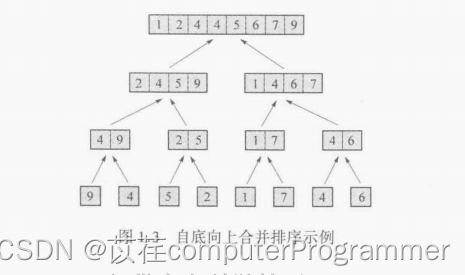
-
更多归并排序内容点击链接查看:归并排序算法
——————END-2022-04-26——————
