42.接雨水
题解
题目:一定一个数组,代码下标位置的高度,求最大接雨水量
思路:
暴力 O(n^2)
1.在当前位置,向左找最大高度,向右找最大高度,取两者较小的
2.用最大高度的较小值 ,减去当前位置的高度,即接雨水量
动态规划O(n)
1.在暴力解法中,每到一个新位置,都要重新查找一遍左右最大值
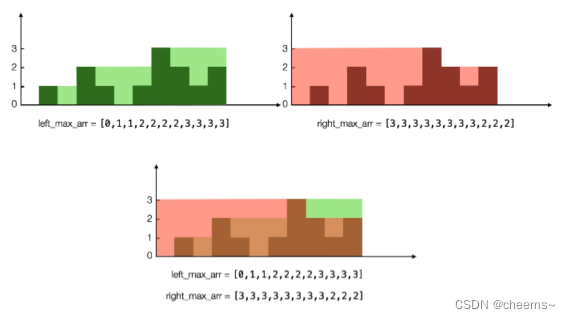
2.我们可以提前将每个位置的左右最大值找出来
3.找出来后一次遍历即可计算答案
4.从后往前遍历一次,记录左边最大值
5.从前往后遍历一次,记录右边最大值
单调栈
1.遍历数组的时候维护一个栈
2.如果当前高度小于等于栈顶,则入栈(意味着当前位置的雨水,被栈顶限制)
3.如果当前高度大于栈顶,则计算栈顶的积水量(当前与栈顶的前一个限定了栈顶的积水量),并弹出栈顶
双指针
1.左右指针指向最左边和最右边
2.如果height[l] < height[r],则积水量是依赖于height[l]的
3.如果height[l] > height[r],则积水量是依赖于height[r]的
4.假设现在是依赖于height[l]
5.如果height[l]>left_max,说明没有积水,更新left_max
6.如果height[l]<left_max,说明有积水,计算积水量,并且记得移动指针
代码
func trap(height []int) int {
ans := 0
n := len(height)
for i := 0; i < n; i++ {
lH, rH := 0, 0
for j := i; j >= 0; j-- {
lH = max(lH, height[j])
}
for j := i; j < n; j++ {
rH = max(rH, height[j])
}
ans += min(lH, rH) - height[i]
}
return ans
}
func max(i, j int) int {
if i > j {
return i
}
return j
}
func min(i, j int) int {
if i > j {
return j
}
return i
}
func trap(height []int) int {
ans, cnt := 0, 0
n := len(height)
lH, rH := make([]int, n), make([]int, n)
for i := 0; i < n; i++ {
cnt = max(cnt, height[i])
rH[i] = cnt
}
cnt = 0
for i := n - 1; i >= 0; i-- {
cnt = max(cnt, height[i])
lH[i] = cnt
}
for i := 0; i < n; i++ {
ans += min(lH[i], rH[i]) - height[i]
}
return ans
}
func max(i, j int) int {
if i > j {
return i
}
return j
}
func min(i, j int) int {
if i > j {
return j
}
return i
}
func trap(height []int) int {
ans := 0
stack := make([]int, 0)
for i, h := range height {
for len(stack) > 0 && h > height[stack[len(stack)-1]] {
top := stack[len(stack)-1]
stack = stack[:len(stack)-1]
if len(stack) > 0 {
break
}
left := stack[len(stack)-1]
curWidth := i - left - 1
curHeight := min(height[left], h) - height[top]
ans += curWidth * curHeight
}
stack = append(stack, i)
}
return ans
}
func min(i, j int) int {
if i > j {
return j
}
return i
}
func trap(height []int) int {
ans, n := 0, len(height)
l, r := 0, n-1
leftHeight, rightHeight := 0, 0
for l < r {
if height[l] < height[r] {
if height[l] > leftHeight { //当前高度比左侧最高还高,则更新左侧最高
leftHeight = height[l]
} else { //当前高度比左侧最高 低, 说明构成凹槽,计算积水量
ans += leftHeight - height[l]
}
l++
} else {
if height[r] > rightHeight {//当前高度比右侧最高还高,则更新右侧最高
rightHeight = height[r]
} else {//当前高度比右侧最高 低,说明构成凹槽,计算积水量
ans += rightHeight - height[r]
}
r--
}
}
return ans
}
