首先,我们先看看一个未知数一个方程的情况,ax=b。
他的解可以有三种情况:
(i)当a0时,对于任意的b都有解x=b/a,且,这个解是唯一的。(这种情况就叫非奇异)
(ii)若a=0,b=0。无论x取多少,等式0x=0恒成立,有无穷多个解。这种情况的有解,但不唯一。
(iii)若a=0,b0,无解。因为,没有x可以让等式0x=b成立。(这种情况叫不相容)
上面举的这个例子,对于方阵来说,也就是nxn矩阵,这三种情况都可能存在。
????????But,对于mxn矩阵,也就是长方形矩阵而言,无论是m>n(方程的个数大于未知数的个数)还是m<n(未知数的个数大于方程的个数)都不会出现上面提到的情形(i),也就是说,对于每一个b,不可能都存在解,且唯一。
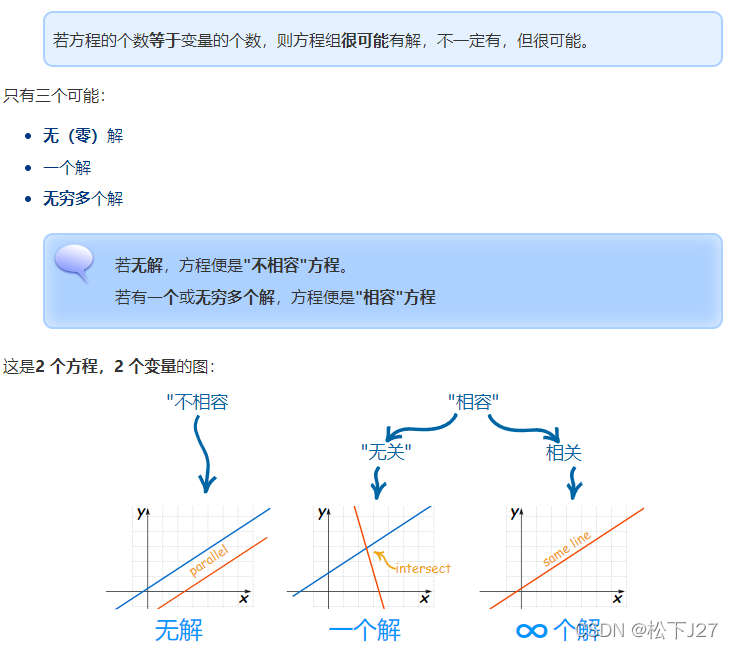
举例:对于如下的3x4矩阵进行消元

?????????按照对于方阵的高斯消元,算到这一步就算不下去了,因为,主对角线上的值为0,且通过换行依然无法避免。就此可以判定为奇异矩阵。
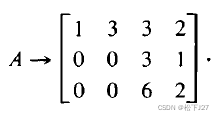
????????但是,对于长方形矩阵,我们继续消元,也就是说,找到消不下去的哪一行的第一个非零元素,把他当作主元,继续消去该主元下面的所有元素。最终得到一个阶梯形矩阵U。
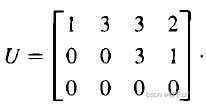
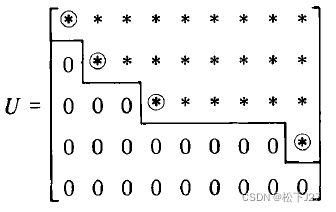
?更一般的情况如下,注意,主元并不一定在主对角线上。(图中画圈的点为主元)
????????同样,这样的阶梯型的上三角矩阵U,也存在一个对应的矩阵L,使得A=LU。注意:L是方阵,他是一个m阶矩阵,等于A和U的行数。如果,在消元过程中有行交换的话,需要引进置换矩阵P。得到PA=LU。

现在我们开始讨论对于有解的b,mxn方程组Ax=b的解:
1,先考虑齐次方程Ax=0的解
对于b=0的情形,消元的过程中方程组的右端b是不变的。最终把Ax=0化简成Ux=0。
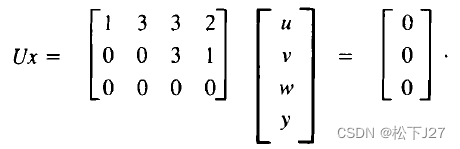
????????我们把四个未知数u,v,w,y分成两组。一组是对应于带有主元的列columns with pivots的变量,称为基本变量basic variables。在本例中,u和w是基本变量。另外一组,是对应于没有主元的列columns without pivots的变量,我们叫他自由变量free variables。在本例中,v,y为自由变量。
????????下面插播一个个人笔记,从中可以清楚的看到,主元列,自由列,以及他们分别对应的基本变量和自由变量。
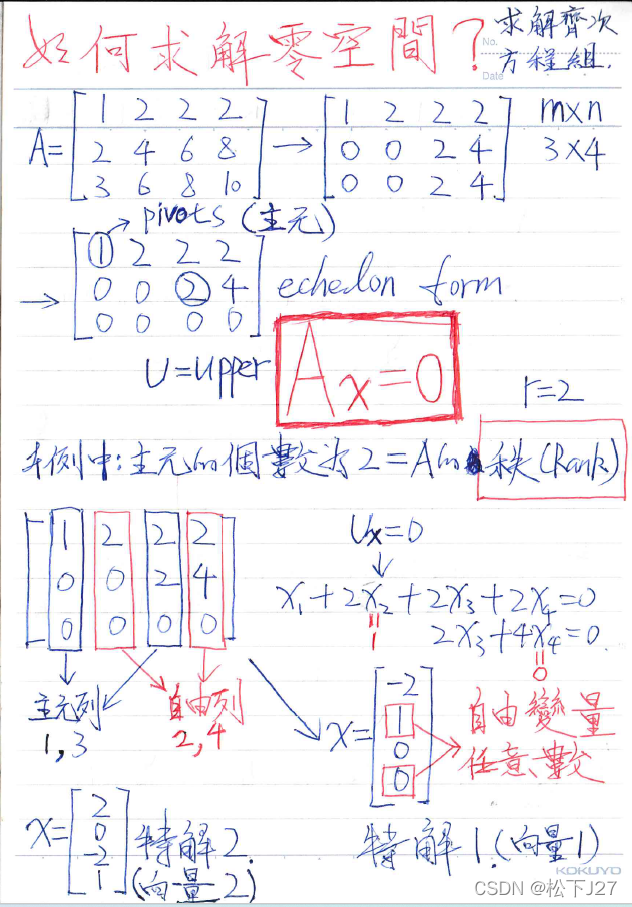

????????为了求得Ux=0(Ax=0)的通解,自由变量可以为任意值,也就说令v,y为已知,再回代到化简后的方程中,基本变量也求出来了,是用v,y来表示的。

?最终求得:
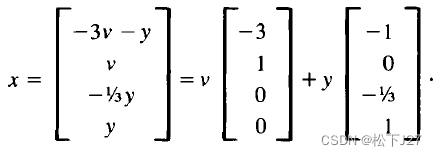
????????可见,该方程Ax=0有无穷多个解,又因为两个自由变量v,y都可以是任意数,该方程组的解具有”双无穷“的特性。也就是说,按住v不动(比如说,令v=1)去改变y,则y有无穷多个解。反之亦然。
? ? ? ? 可以看到,如果我们令v=0,y=1,则向量[-3 1 0 0]'就是齐次方程Ax=0的解,如果令v=1,y=0,则向量[-1 0 -1/3 1]’是齐次方程的解。不难看出,不论怎么调整权重v,y,最终的结果都是Ax=0的解。这就好比Ax=b的列空间C(A),矩阵的列空间指出,所有可能的右端b,都是通过对A中各列线性组合得到的。只不过,到了这里,参与线性组合的向量不是A的列向量而是Ax=0的解,零向量。同时,这些零向量或者叫他们解x的向量,他们的维度也和A中各列的维度不同。用于合成C(A)的列向量的维度是m(等于b的维度),而这里的解x的向量,他们的维度是n,等于A的列数,也等于未知数的个数。
? ? ? ? 对于这个例子,在四个未知数所构成的四维空间中,Ax=0的解,构成了一个二维子空间---A的零空间。这个空间是由[-3 1 0 0]'和[-1 0 -1/3 1]'所张成的一个二维平面。
? ? ? ? 因此,我们可以得出如下结论:对于一个列数大于行数(未知数的个数大于方程的个数的方程组)的矩阵,即n>m的矩阵。由于最多只能m个非零主元(每行一个),因此,至少有n-m个自由变量,当U存在全零行时出现。自由变量的个数可以多余n-m个,对于这个例子就是的,4-3=1,但自由变量有两个。
? ? ? ? 对于未知数个数大于方程个数的方程组,齐次方程组Ax=0,必有除了x=0以外的非平凡解。其中,零空间的维数等于自由变量的个数。
2,现在考虑非齐次方程组Ax=b的解
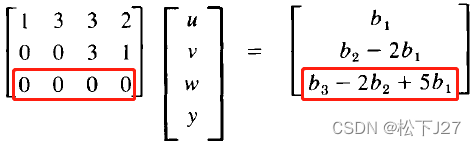
按照相同的步骤对方程左右两边化简,得到Ux=c
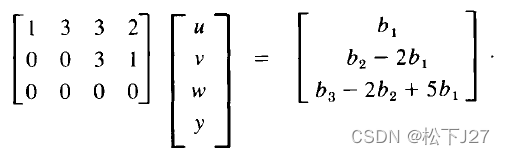
?对于所有有解的b而言,应该是由A的各列所张成的。(注意:不是U的列)
????????很明显,尽管这里有四个列向量,但是我们的b是三维的,也就是说,最多只能张成一个三维空间或者是三维空间的一个子空间。又因为,col2=3*col1, col4=col1+col3/3(也就是前面的自由列),因此,最终他是由col1和col3所张成的三维空间中的一个二维子空间。另一方面,要想方程有解,则必须要保证最后一组方程成立,如果b3-2b2+5b10,则该方程组就无解。满足方程b3-2b2+5b1=0的所有点(b1,b2,b3)构成了一个平面。这一平面和前面所张成的平面一模一样。同时,向量[5,-2,1]'垂直于这一平面,因而也垂直于A的每一列。
? ? ? ? ?现在,假定b在A的列空间中,显然要保证最后一行方程为0=0。和前面一样,经过高斯消元后,用自由变量v,y(已知数)来表示基本变量u,w。

?得到如下解:

(上图为非齐次方程的解)
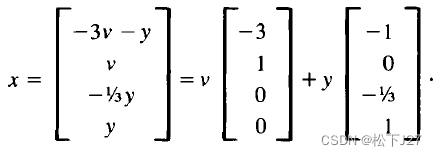
?(上图为齐次方程的解)
????????与之前算出的齐次方程的解相比,多了一组向量,用红色的方框标注,这个向量是Ax=b的一个特解(这个特解就是保证最后一组方程的约束b3-2b2+5b1=0的一个解)。而,齐次方程Ax=b的通解,是Ax=b的这个特解和Ax=0的通解的和。
? ? ? ? 注意,这里所说的特解是前面提到的"满足方程b3-2b2+5b1=0的所有点(b1,b2,b3)构成了一个平面。"平面中的一个点,该平面上的任意一点,都可以作为Ax=b的特解。
? ? ? ? 例如,为满足b3-2b2+5b1=0,我们找到一个点b1=1,b2=5,b3=5,满足该约束。并得到如下矩阵Ax=b:

?经过高斯消元后,得到:
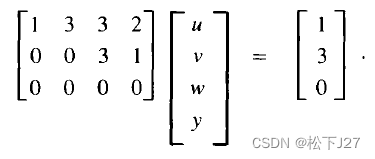
?最后一行满足0=0:

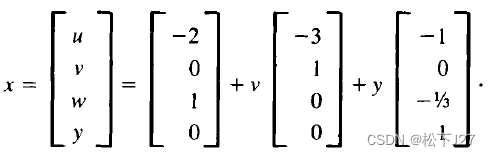
?这个解依然具有“双无穷”的特性。从几何的角度讲,Ax=b的通解是四维空间中的一个平面,但他不是一个子空间。因为,这个平面不过原点。这个平面与零空间的平面平行,但不重合。他沿着特解移动了一段。

以下是个人笔记的补充:



?(全文完)?
作者 --- 松下J27
鸣谢:
1,linear algebra and its application -?GILBERT STRANG
2,线性代数及其应用 - 侯自新,南开大学出版社,1990版
(*配图与本文无关*)?
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。
