本篇文章记录数据结构实验内容-----无向图的深度和广度优先遍历。
代码:
#include<bits/stdc++.h>
using namespace std;
#define mvnum 100
#define maxsize 100
//#define OVERFLOW -1
#define ERROR 0
#define OK 1
typedef char VerTexType;
typedef int ArcType;
typedef int status;
typedef int Eelemtype;
typedef struct
{
Eelemtype *base;
int front;
int rear;
}Squeue;//定义队列
typedef struct
{
VerTexType vexs[mvnum];//顶点表
ArcType arcs[mvnum][mvnum];//邻接矩阵
int vexnum,arcnum;//图的点数和边数
}AMGraph;
Squeue q;
status initqueue(Squeue &q)//初始化队列
{
q.base=new Eelemtype[maxsize];
if(!q.base) exit(-1);
q.front=q.rear=0;
return OK;
}
status push(Squeue &q,Eelemtype e)//进队操作
{
if((q.rear+1)%maxsize==q.front)
return ERROR;
q.base[q.rear]=e;
q.rear=(q.rear+1)%maxsize;
return OK;
}
status pop(Squeue &q,Eelemtype e)//出队操作
{
if(q.front==q.rear) return ERROR;
e=q.base[q.front];
q.front=(q.front+1)%maxsize;
return OK;
}
status empty(Squeue &q)//判断队列是否为空
{
if(q.front!=q.rear)
return 1;
else return 0;
}
Eelemtype gethead(Squeue q)//取出队列的队首元素值
{
if(q.front!=q.rear)
return q.base[q.front];
}
int locate(AMGraph &G,int v)//在建立无向图的时候用于求下标
{
for(int i=0;i<G.vexnum;i++)//在所有点中寻找
{
if(i==v)//与所求的下标相等则直接返回
return i;
}
}
int v1,v2,w;
void createudn(AMGraph &G)//创建无向图
{
cout<<"请输入无向图的点数和边数"<<endl;
cin>>G.vexnum>>G.arcnum;
cout<<"请输入各顶点"<<endl;
for(int i=0;i<G.vexnum;i++)
cin>>G.vexs[i];//在顶点数组中输入顶点
for(int i=0;i<G.vexnum;i++)
for(int j=0;j<G.vexnum;j++)
{
G.arcs[i][j]=0;//无向图是将每个边赋值为0
}
cout<<"请输入无向图邻接结点"<<endl;
for(int k=0;k<G.arcnum;k++)
{
cin>>v1>>v2;
int i=locate(G,v1);int j=locate(G,v2);//求出顶点v1和v2的下标
G.arcs[i][j]=1;//利用求出的下标赋权值
G.arcs[j][i]=G.arcs[i][j];//针对无向图的语句
}
}
bool visited[100];//辅助标记数组
void dfs(AMGraph G,int v)//深度优先遍历
{
cout<<G.vexs[v]<<" ";
visited[v]=1;
for(int j=0;j<G.vexnum;j++)
{
if(G.arcs[v][j]&&!visited[j])
dfs(G,j);
}
}
void dfstravel(AMGraph G)//对所有的连通分量进行遍历
{
for(int v=0;v<G.vexnum;v++)
visited[v]=0;//辅助标记数组初始化全为0
for(int v=0;v<G.vexnum;v++)
if(!visited[v]) dfs(G,v);
}
void bfstravel(AMGraph G)//广度优先遍历无向图
{
for(int v=0;v<G.vexnum;v++)
visited[v]=0;
for(int v=0;v<G.vexnum;v++)//对所有联通分量进行操作
{
if(!visited[v])
{
cout<<G.vexs[v]<<" ";
visited[v]=1;
push(q,v);//进队
while(empty(q)==1)//队列非空时
{
Eelemtype t=gethead(q);//取出队首元素
// cout<<t<<" ";
pop(q,t);//队首元素出队
for(int j=0;j<G.vexnum;j++)
{
if(G.arcs[t][j]==1&&!visited[j])
{
cout<<G.vexs[j]<<" ";
visited[j]=1;
push(q,j);
}
}
}
}
}
}
int main()
{
int ch;
AMGraph G;
initqueue(q);
cout<<"请输入你要选择的操作:"<<endl;
cout<<"1.创建无向图"<<endl;
cout<<"2.输出图的深度优先遍历结果"<<endl;
cout<<"3.输出图的广度优先遍历结果"<<endl;
cin>>ch;
while(ch!=4)
{
switch(ch)
{
case 1:createudn(G);
cout<<"无向图创建成功!";
cout<<endl;
break;
case 2:cout<<"无向图的深度优先遍历结果为:"<<endl;
dfstravel(G);
cout<<endl;
break;
case 3:cout<<"无向图的广度优先遍历结果为:"<<endl;
bfstravel(G);
cout<<endl;
break;
}
cin>>ch;
}
return 0;
}例子:
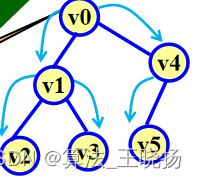
输入:
6 5
0 1 2 3 4 5
0 1
1 2
1 3
0 4
4 5?输出显示:
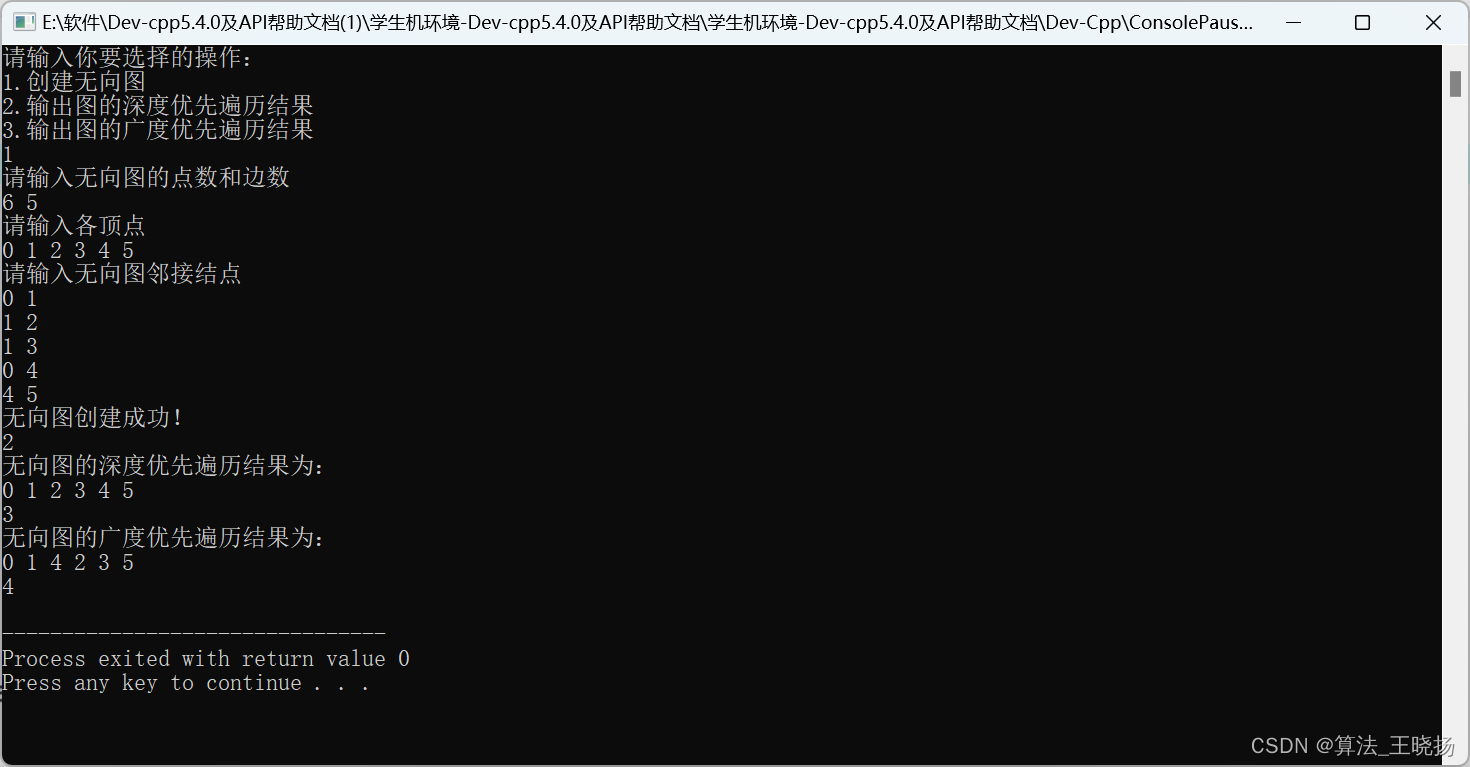
完结!?
