一、题目

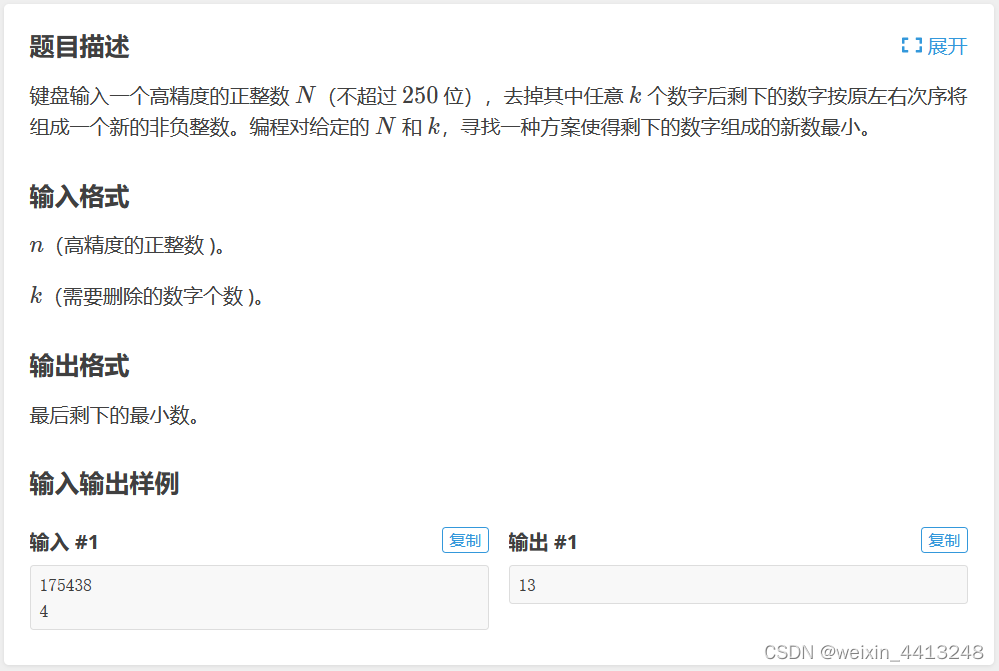
在这里插入图片描述

二、解题思路

首先想到使用暴力求解，显然所有情况共 $A_N^k$ 种，计算量比较大，很有可能超时。
该题为从N个数中取k个数，对于这种问题，应当想到是否可用动规解决。分析发现，对于该问题来说，后面的结果不影响前面的结果，具体来说，假设已经从前i个数中取了j个数，随后我们在i+1~N中取数字的时候，不管怎么取，前i个数的结果都是确定的，不会因为后面取什么数而改变，因此，可以确定该题能使用动规解决。
假设dp[i][j]表示前j个数中，取i个数后的最优解。由于该题的数字很大，显然无法使用int存储，此时想到两种解决方案：高精度数组存储和字符串，显然后者更优。
接下来需要确定动规方程。分析可以发现，对于每个数，就两种选择，保留或者不保留。当从前j个数中去掉i个数时，对于第j个数，如果保留，那么最优结果就是dp[i][j-1]+N[j]（N[i]表示第i个字符），如果不保留，那么最优结果就是dp[i-1][j-1]，由此可得dp[i][j]=min{dp[i][j-1]+N[j]，dp[i-1][j-1]}。
当你以为结束的时候，实际还没完。有两种特殊情况需要处理：当数为10001，k=2时，输出结果为000，实际上应该为0；当数位10001，k=1时，输出结果为0001，实际上应当为1。

三、代码

#include<iostream>
#include<string>
#include<vector>
#include<map>
#include<algorithm>
#include<cmath>
using namespace std;

int main(){
    string N;
    int k;
    cin>>N>>k;
    int len=N.size();
    string dp[251][251]={""};
    string init="";
    for(int i=1;i<=len;i++){
        init+=N[i-1];
        dp[0][i]=init;
    }
    for(int i=1;i<=k;i++){
        for(int j=i+1;j<=len;j++){
            string first=dp[i][j-1]+N[j-1];
            string second=dp[i-1][j-1];
            if(first<second)
                dp[i][j]=first;
            else
                dp[i][j]=second;
        }
    }
    int flag=true;
    for(int i=0;i<dp[k][len].size();i++){
        if(dp[k][len][i]=='0'&&flag)continue;
        cout<<dp[k][len][i];
        flag=false;
    }
    if(flag)cout<<0;
}