[数据结构与算法] Run Run Run

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> Run Run Run -> 正文阅读

[数据结构与算法]Run Run Run

学习了 2022 年集训队论文《浅谈与 Lyndon 理论有关的字符串组合问题》
写得很好，像我这样的字符串小白也能看懂

Lyndon 分解

若字符串 $w$ 小于它的每一个真后缀，则称 $w$ 是 Lyndon 串。
若字符串 $w$ 是 Lyndon 串，则 $w^kw'$ 是近似 Lyndon 串，其中 $w^{'}$ 是 $w$ 的前缀。

串 $w$ 可以分解位 $w_1^{c_1}\dots w_{k}^{c_k}$ ，其中 $w_1>\dots>w_k$ 。

最小后缀族：对于串 $w$ 的后缀 $w^{'}$ ，若存在 $u$ 使得任意后缀 $w^{''}$ 满足 $w^{'} u < w^{''} u$ ，则 $w^{'}$ 是 $w$ 的一个有效后缀，有效后缀的集合称为 $w$ 的最小后缀族，记为 $S S (w)$

若 $u^2v,uv,v$ 都是 $w$ 的后缀，则 $u v$ 不是有效后缀。
若 $u,v\in SS(w),|u|<|v|$ ，则 $u$ 是 $v$ 的 $b o r d e r$ ，且 $2|u|\le |v|$ 。
有效后缀形如 $s_i=w_i^{c_i}\dots w_k^{c_k}$
$s_{i+1}$ 是 $s_i$ 的前缀的充要条件是 $i\le \lambda$ ，其中 $s_{\lambda}$ 是对 $w$ 进行 Duval 算法时第一次比较完字符串末尾时的近似 Lyndon 后缀。（因为 $w_i^xs_{i+1}$ 是近似 Lyndon 后缀，所以 $s_{i+1}$ 是 $w_{i}$ 的前缀）

后接 $v$ 的最小后缀：

给定 $w, v$ ，求 $w$ 的后缀 $u$ ，使得 $u v$ 最小，记为 $M i n s u f (w, v)$

由于 $u$ 是 $s_{\lambda},\dots,s_k$ 之一，另 $w_i=s_{i+1}+y_i$ ， $x_i=y_i+s_{i+1}$ ，则有 $s_i=s_{i+1}+x_i^{c_i}$ 。

$\forall i\in [\lambda,k-1],y_i>x_{i+1}^{\infty}$ ，即证 $s_{i+1}y_i>s_{i+1}x_{i+1}^{\infty}$ ，即 $w_i>w_{i+1}^{\infty}s_{i+2}$ ，又有 $w_i>w_{i+1}^{\infty}$ 。
$\forall i\in [\lambda,k-1],x_i^{\infty}>x_{i+1}^{\infty}$

考虑比较 $s_iv$ 和 $s_{i+1}v$ 的大小，发现这等价与比较 $x_i^{c_i}v$ 和 $v$ 的大小，这等价于比较 $x_i^{\infty}$ 和 $v$ 的大小，故可以二分找到一个 $i$ 使得 $x_i^{\infty}>v>x_{i+1}^{\infty}$ ，此时 $Minsuf(w,v)=s_{i+1}v$ 。

例：JSOI 2019 节日庆典，求每个前缀的最小表示。
线性做法：考虑当前串可以表示成 $uw^kw'$ ，那么只需要考虑最小表示开头为 $w^kw'$ 或开头在 $w^{'}$ 里面的情况，在 $w^{'}$ 里面时发现去掉最后 $∣ w ∣$ 个字符即为 $uw^{k-1}w'$ 的循环表示，是之前已经求出的答案。

Runs

Runs 的定义和 Runs 定理

定义：本源串， $k$ 次方串，平方串，本源 $k$ 次方串。
Runs：对于字符串 $S$ ，若其一个子串 $S [i, j]$ 具有最小周期 $p$ ，满足 $2p\le j-i+1$ ，且 $S_{i-1}\neq S_{i+p-1}，S_{j+1}\neq S_{j+1-p}$ ，则 $r = (i, j, p)$ 构成 $S$ 的一个 run， $e_r=\frac{j-i+1}{p}$ 为它的指数， $S$ 的所有 runs 的集合记为 $R u n s (S)$ 。
Runs 为研究幂串结构提供了方法，容易发现我们定义的 runs 满足 run 里面至少有一个平方串。

周期相同的两个 runs 的交长度 $< p$ 。
任何一个 run $r = (i, j, p)$ 可以导出 $j ? i + 1 ? 2 p$ 个本源平方串，每个本源平方串由唯一一个 run 导出

下面，我们将证明两个重要的命题：
Runs 定理：记 $\rho(n)$ 和 $\sigma(n)$ 表示长为 $n$ 的串的 runs 个数以及 runs 指数和的最大值，有 $\rho(n)<n,\sigma(n)<3n$ 。

记 $_0,<_1$ 为字符集上两种相反的序。

定义 Lyndon 根：对于一个 run $r = (i, j, p)$ ，若在字典序 $<$ 下其长为 $p$ 的子串 $S [u, u + p ? 1]$ 为 Lyndon 串，则称 $S [u, u + p ? 1]$ 是 $r$ 关于 $<$ 的一个 Lyndon 根。
定义 Lyndon 数组：定义 $l_t(i)$ 表示在 $_t$ 下左端点为 $i$ 的最长 Lyndon 串的右端点，将 $l_t(i)$ 成为 $S$ 的 Lyndon 数组。
性质： $l_0(i),l_1(i)$ 恰有一个为 $i$ ，证明略。
性质：对于 run $r = (i, j, p)$ ，设 $S_{j+1}<_tS_{j+1-p}$ ，那么其任意 Lyndon 根 $S [u, u + p ? 1]$ 有 $l_t(u)=u+p-1$ 。证明：对于 $S[u,v],u+p-1<v\le j$ 满足其为 $w^kw'$ ，对于 $v > j$ 显然不是 Lyndon 串。
定义 Lyndon 根：若 run $r = (i, j, p)$ 的 Lyndon 根 $S [u, u + p ? 1]$ 满足 $u > i$ ，那么其为真 Lyndon 根。
性质： $S[u,l_0(u)],S[u,l_1(u)]$ 不可能同时为两个 run 的 Lyndon 根。证明：设 $l_0(u)=u$ ，则有 $S_u=S_{u-1}+S_{u+p-1}=S_{l_1(u)}$ ，故 $S[u,l_1(u)]$ 不是 Lyndon 串。
性质：任意两个不同的 run 的真 Lyndon 根左端点集合不交。（由上一条得到）

Runs 的求解方法

算法 1：枚举周期 $p$ ，用 NOI2016 优秀的拆分的做法解决。
算法 2：由于 runs 的 Lyndon 根一定形如 $S[i,l_t(i)]$ ，所以先求出 Lyndon 数组再进行扩展即可。求 Lyndon 数组可以考虑一种从后向前构造 Lyndon 分解的方法，即从后往前扫，维护一个单调栈，每次加入一个字符，检查能不能和栈顶的串合并。

幂串的结构

性质：若 $u^2,v^2,w^2$ 是本源平方串，且 $u^2$ 是 $v^2$ 的前缀， $v^2$ 是 $w^2$ 的前缀，则 $|w|\ge |u|+|v|$ 。

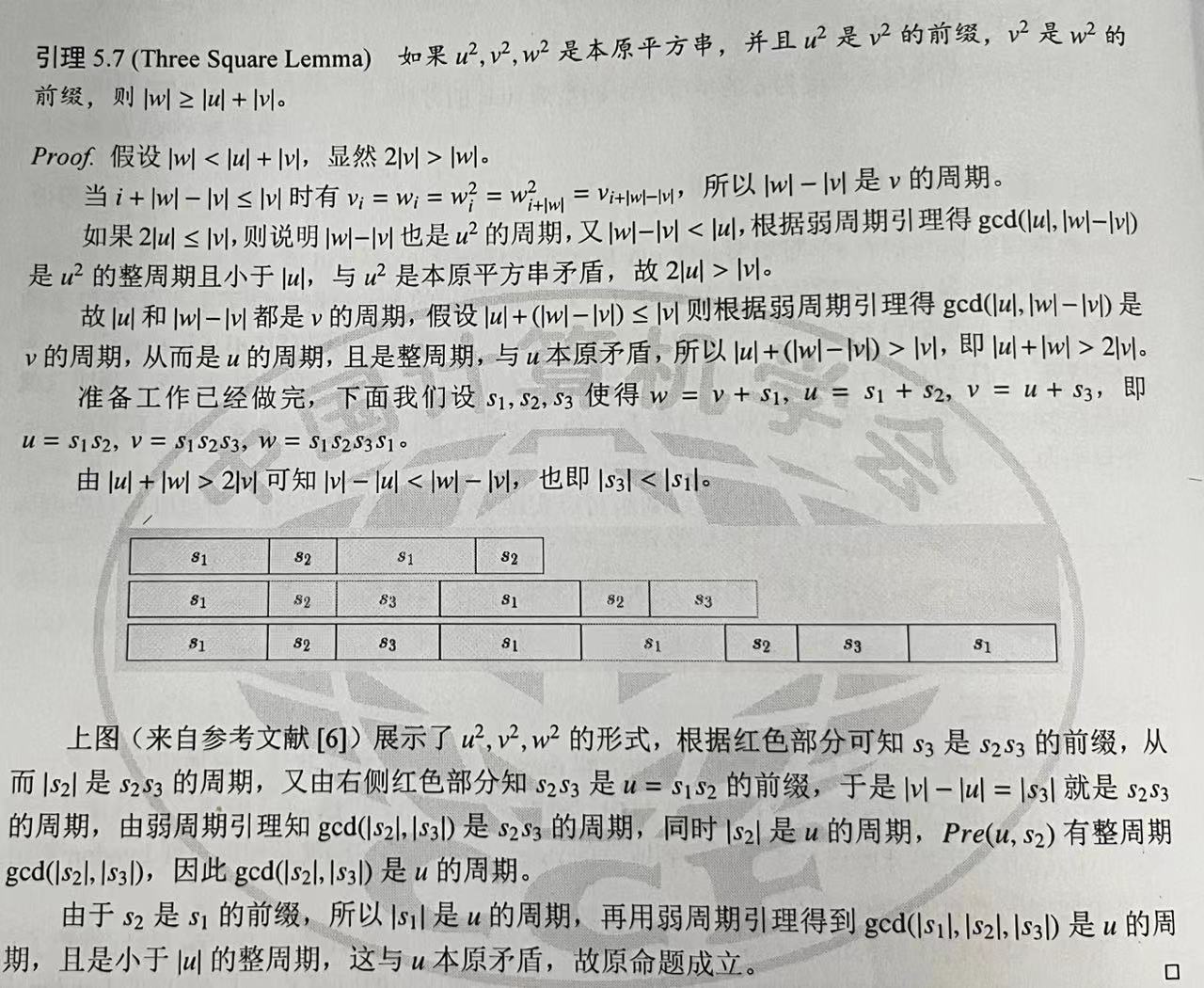
于是我们有结论：串 $w$ 的本源平方前缀个数为 $O(\log |w|)$ 个。
串 $w$ 的本源平方串个数为 $O(|w|\log |w|)$ 个，于是也有 $\sum_r （j-i+1-2p)$ 为 $O(|w|\log |w|)$ 。

性质：字符串 $w$ 的本质不同本源平方串个数为 $O (∣ w ∣)$ 。证明：考虑最后一次出现位置，假设一个左端点有 3 个 $u, v, w$ ，则有 $2|u|\le |w|$ ，那么 $u^2$ 不是最后一次出现。

例：ZJOI 2020 字符串，区间询问本质不同平方串。

先忽略本质不同，考虑 run $r = (i, j, p)$ ，其每个 $S [l, l + 2 k p ? 1]$ 都可以作为一个贡献。将 $(l, l + 2 k p ? 1)$ 看作一个点，那么对于一个 $k$ ，我们可以将操作看成斜线加，加的次数是 $\sum_r \frac{j-i+1}{p}$ ，其为 $O (n)$ 。
下面考虑本质不同，对于两个相同子串 $S [i, i + 2 p ? 1], S [j, j + 2 p ? 1]$ ，我们在 $(i, j + 2 p ? 1)$ 放一个权值为 $? 1$ 的点即可。在一个 run 里面的同样只需要枚举 $k$ 然后斜线减，否则就是和前面一个 run 里面的相同。从做到右扫 runs，我们只关注 run 里面第一次出现的平方串，容易发现其个数为 $\sum_r (j-i+1-2p)\sim O(n\log n)$ ，故直接使用 hash，然后在平面上会添加 $O(n\log n)$ 个点。时间复杂度 $O(n\log^2 n+q\log n)$ 。

Lyndon 树

对于一个 Lyndon 串 $w$ ，我们可以得到一个 $2 ∣ w ∣ ? 1$ 个结点的二叉树，每个结点代表一个子串（且也为 Lyndon 串），构建的方法为找到 $w = u + v$ ，其中 $v$ 是 $w$ 的最小后缀，然后 $u, v$ 为 $w$ 的两个儿子。

构建方法：从后向前，维护 $[i + 1, n]$ 组成的森林（每一个子树是一个 Lyndon 串），加入当前字符 $S_i$ ，会合并栈顶的一些 Lyndon 串，将这些点串起来即可。

性质：以 $i$ 为左端点的最长 Lyndon 子串对应 Lyndon 树中以 $i$ 为左端点的最大子树。（证明：建树的过程和求 Lyndon 数组相同）
性质：若 $S [l, r]$ 是 Lyndon 串，则 $l,\dots,r$ 的 LCA 的子树的左端点为 $l$ 。

区间短周期查询：每次查询 $S [l, r]$ 的最小周期，若最小周期大于一半则不用输出。

这等价与查询是否有一个包含 $[l, r]$ 且周期不超过 $\frac{r-l+1}{2}$ 的 run。
以 $_0,<_1$ 两种比较关系建 Lyndon 树，分别求出 $l,\dots,\lceil \frac{l+r}{2}\rceil$ 的 LCA，检查以其右子树为 Lyndon 根的 runs。
证明：我们只需要找到一个包含 $m$ 的 Lyndon 根。 LCA 的右子树 $x$ 满足条件，若其不为答案的 runs $r = (i, j, p)$ ，那么我们知道 $x$ 的右端点大于 $j$ ，但是 $S_{j+1}<S_{j+1-p}$ ，这与 $x$ 的子树是 Lyndon 串矛盾。

Lyndon 串计数

记 $\hat w$ 为 $w$ 的最小表示，若 $\hat w=w$ 则称 $w$ 为 necklace。
性质：每个 Lyndon 串都是 necklace，每个 necklace 可以写成 $w^k$ 其中 $w$ 是 Lyndon 串。

$\hat w$ 的求法：首先找到 $u^k=w$ 然后求 $\hat u$ ，只需要对 $u u$ 求 Lyndon 分解，然后找到最后一个在 $[1, ∣ u ∣]$ 中分解的地方 $x$ ，那么 $\hat u=u[x,|u|]+u[1,x-1]$ 。

求前驱 necklace：求长度等于 $∣ w ∣$ 字典序 $\le w$ 的最大的 necklace。记作 $P L (w)$

$P L (w)$ 形如 $Pre(w,i-1)+P(w_i)+z^{|w|-i}$ ，其中 $P (c)$ 表示比 $c$ 小的最大字符，故我们有 $w|^2$ 的做法，即每次判断是不是 necklace。
考虑优化判断的过程，只需要判断 $Pre(w,i-1)+P(w_i)$ 是不是近似 Lyndon 串即可，用一次 Duval 算法就可以解决。

Lyndon 串计数：
设 $P (n), L (n)$ 表示本源串和 Lyndon 串的数量，有 $L(n)=\frac 1n P(n)$ ，且 $\Sigma^n=\sum _{d\mid n}P(d)$ ，那么 $L(n)=\frac 1n \sum_{d\mid n}\mu(\frac nd)\Sigma^d$ 。

Lyndon 串排名：
设 $P (d), P^{'} (d)$ 表示满足 $\hat u^{n/d}\le w$ 的任意串 $u$ 的数量，以及本源串 $u$ 的数量。
$rank=\frac 1nP'(n),P(x)=\sum_{d\mid x}P'(d)\to rank=\frac 1n\sum_{d\mid n} \mu(\frac nd)\times P(d)$ 。
容易发现 $P (d)$ 等价与 $\hat u\le Pre(w,d)$ 的任意串数量。
识别自动机： KMP 的改版，当转移字符等于 $w_i$ 时，到 $i + 1$ ，小于 $w_i$ 时到 $n$ ，否则到 0。

性质： $w$ 是 necklace， $\hat u\le w,|u|=|w|=n$ 当且仅当 $u^{2}$ 中存在一个不为 $w$ 真前缀的子串 $v$ 满足 $v\le w$ 。
性质： 发现对于 necklace 的识别自动机，它和 KMP 自动机一样。

对于计算 $P (n)$ ，我们只需要考虑不能转移到 $n$ 的点有多少，我们会发现，考虑串 $u^{\infty}$ 对于充分打大的 $j$ ， $j$ 转移到的点和 $j + ∣ u ∣$ 转移到的是一样的。
我们定义 $j ∣ u ∣$ 转移到的点 $t$ 为这个串的起始点，现在就是要求环的数量。设 $f_j$ 为长为 $j$ 的环的数量，枚举第一个环 $j$ ，有 $f_i=\sum_{j=1}^{min(n-1,i)} b_jf_{i-j}$ ，其中 $b_j$ 表示从这个点转移到 0 的边数。容易发现可以使用多项式求逆来解决。于此同时，答案为 $\sum_{i=1}^{n-1} i\times b_i\times f_{n-i}$ 。注意到也可以使用线性递推做到 $O(n\log n\log m)$ 的复杂度。