页面置换算法
先进先出算法(FIFO): 先进先出算法是最简单的分页替换算法,是指每次有新的分页需要调入时,会选择调入内存时间最久的分页换出。它简单,容易实现,但这种绝对的公平方式容易导致效率的降低。
--------发生缺页中断时,即最先进来的淘汰出去
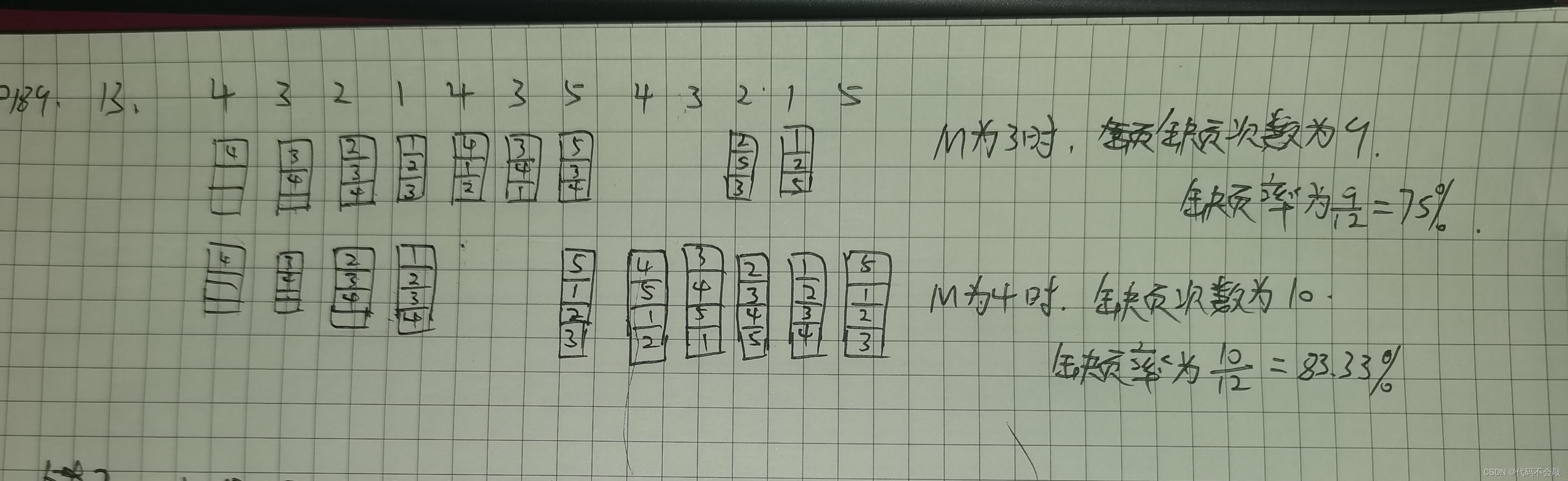
最近最久未使用算法(LRU)算法: 即最近最少使用,是一种常用的页面置换算法,选择最近最久未使用的页面予以淘汰。该算法赋予每个页面一个访问字段,用来记录一个页面自上次被访问以来所经历的时间 t,当须淘汰一个页面时,选择现有页面中其 t 值最大的。即最近最少使用的页面予以淘汰。
--------发生缺页中断时,选择未使用时间最长的页面置换出去

最佳置换算法(OPT): 这是一种理想情况下的页面置换算法,但实际上是不可能实现的。
--------发生缺页中断时,看后面在物理块中的页面序列,查看谁出现的最晚,谁被淘汰。
大家可以做几道例题就基本理解了。
以下是这三种算法的模拟,使用的是队列存储和set进行查询;对于效率不是特别好,只是一个基本的模拟
要求: 设计主界面以灵活选择某算法。2.用随机数方法产生页面走向。3.假定初始时页面都不在内存。
内容: 编程序实现先进先出算法(FIFO)、最近最久未使用算法(LRU)算法、最佳置换算法(OPT)的具体实现过程,并计算访问命中率。
代码如下:
#include<bits/stdc++.h>
using namespace std;
vector<int> a; //随机数产生的页面走向
queue <int> q; //存页面--模拟
unordered_set<int> se; //队列存在的数
int cnt; //缺页次数
int Size; //物理块数
int option; //菜单选择
int n; //页面序列的个数
void init()
{
cnt = 0;
se.clear();
while (!q.empty()) q.pop();
}
void Print(queue<int> qq)
{
while (!qq.empty())
{
printf("%d ", qq.front());
qq.pop();
}
puts("");
}
void FIFO()
{
init();
for (int i = 0; i < a.size(); i++)
{
if (se.count(a[i])) //此页面已存在,无需操作
{
printf(" 无中断,命中:");
Print(q);
continue;
}
se.insert(a[i]);
if (q.size() == Size)
{
se.erase(q.front());
q.pop();
}
cnt++;
q.push(a[i]);
printf(" 第%d次缺页中断:", cnt);
Print(q);
}
printf(" FIFO算法缺页次数:%d, 缺页率:%%%.2lf\n", cnt, 1.0*cnt/n*100);
printf(" FIFO算法命中次数:%d, 命中率:%%%.2lf\n", n-cnt, (1 - 1.0*cnt/n) * 100);
}
void LRU()
{
init();
for (int i = 0; i < a.size(); i++)
{
if (se.count(a[i])) //此页面已存在,进行更新
{
queue <int> p;
while (!q.empty())
{
int x = q.front();
q.pop();
if (x == a[i]) continue;
p.push(x);
}
q = p;
q.push(a[i]);
printf(" 无中断,命中:");
Print(q);
continue;
}
se.insert(a[i]);
if (q.size() == Size)
{
se.erase(q.front());
q.pop();
}
cnt++;
q.push(a[i]);
printf(" 第%d次缺页中断:", cnt);
Print(q);
}
printf(" LRU算法缺页次数:%d, 缺页率:%%%.2lf\n", cnt, 1.0*cnt/n*100);
printf(" LRU算法命中次数:%d, 命中率:%%%.2lf\n", n-cnt, (1 - 1.0*cnt/n) * 100);
}
void OPT()
{
init();
for (int i = 0; i < a.size(); i++)
{
if (se.count(a[i])) //已经存在,不进行操作
{
printf(" 无中断,命中:");
Print(q);
continue;
}
if (q.size() < Size)
{
cnt++;
se.insert(a[i]);
q.push(a[i]);
printf(" 第%d次缺页中断:", cnt);
Print(q);
continue;
}
unordered_set<int> t;
queue <int> p;
for (int j = i + 1; j < a.size(); j++)
{
if(!se.count(a[j])) continue;
if (t.size() == Size - 1) break;
t.insert(a[j]);
}
int f = 1;
while (!q.empty())
{
int x = q.front();
q.pop();
if (!t.count(x) && f)
{
se.erase(x);
f = 0;
continue;
}
p.push(x);
}
q = p;
q.push(a[i]);
se.insert(a[i]);
cnt++;
printf(" 第%d次缺页中断:", cnt);
Print(q);
}
printf(" OPT算法缺页次数:%d, 缺页率:%%%.2lf\n", cnt, 1.0*cnt/n*100);
printf(" OPT算法命中次数:%d, 命中率:%%%.2lf\n", n-cnt, (1 - 1.0*cnt/n) * 100);
}
void menu()
{
printf("-------------------------菜单-----------------------------\n");
printf(" 1、随机产生作业和物理块数\n");
printf(" 2、自己输入作业和物理块数\n");
printf(" 3、先进先出算法(FIFO)\n");
printf(" 4、最近最久未使用算法(LRU)\n");
printf(" 5、最佳置换算法(OPT)\n");
printf(" 6、重现菜单\n");
printf(" 0、退出系统\n");
printf(" 请注意:在选择过1或2后才能选择3、4、5,否则会发生错误!\n");
}
void random()
{
a.clear();
srand((unsigned) (time(NULL))); //随机数更新
Size = rand()%5 + 2; //随机数[2, 6]
n = rand()%20 + 5; //随机数[5, 24]
printf("分配的物理块数为%d,页面序列共%d个,如下:\n", Size, n);
for (int i = 0; i < n; i++)
{
int x = rand()%(n / 2) + 1; //随机数[1, n / 2]
a.push_back(x);
printf("%d ",x);
}
puts("");
}
void Scanf()
{
a.clear();
printf("请问输入分配的物理块数:") ;
scanf("%d", &Size);
printf("请问页面序列共多少个:");
scanf("%d", &n);
printf("请输入:");
for (int i = 0; i < n; i++)
{
int x; scanf("%d", &x);
a.push_back(x);
}
}
int main()
{
menu();
while(1)
{
printf("请选择:");
scanf("%d", &option);
if (option == 0)
{
printf("\n 成功退出!!\n");
break;
}
switch (option)
{
case 1: random(); break;
case 2: Scanf(); break;
case 3: FIFO(); break;
case 4: LRU(); break;
case 5: OPT(); break;
case 6: menu(); break;
default: printf("输入错误,请您确认无误后再次输入!\n");
}
}
return 0;
}
结果截图:

如果有错误,欢迎大哥们指出来!!
