机器人的运动范围-剑指offer
地上有一个rows行和cols列的方格。坐标从[0,0]到[rows-1,cols-1]。一个机器人从坐标[0,0]的格子开始移动,每一次只能向左、右、上、下四个方格移动一格,但是不能进入行坐标和列坐标的数位之和大于threshold的格子。例如,当threshold为18时,机器人能够进入方格[35,37],因为3+5+3+7=18.但是,它不能进入方格[35,38]。因为3+5+3+8=19.请问该机器人能够达到多少个格子?
dfs(深度优先搜索)
class Solution:
#dfs
def movingCount(self,m,n,k):
res=set()#存的是满足要求的所有的点的集合
def dfs(i,j):
#i不能超过坐标m,j不能超过坐标n,
#行坐标和列坐标的数位之和不能超过k,
#res存的是已经遍历过的点
#(i,j)必须是不存在res中的
if i==m or j==n or i//10+i%10+j//10+j%10>k or (i,j) in res:
return
#如果满足这四种要求之一,直接return就行,表明已经到到最大深度
res.add((i,j))#吧当前坐标加进去res
dfs(i+1,j)#然后在给该坐标四周的坐标进行dfs
dfs(i,j+1)
dfs(0,0)#最开始的dfs坐标
return len(res)
#bfs
def movingCount2(self,m,n,k):
res=set()
queue=[(0,0)]#队列,存满足要求的坐标点
while queue:#当这个queue里面有数就一直判断,直到没有
i,j=queue.pop(-1)#用i,j接受queue弹出来的变量
if i//10+i%10+j//10+j%10<=k and (i,j) not in res:
res.add((i,j))#满足上面条件,则吧坐标点加进res里
if i+1<m and j<n:#如果该点的下边坐标满足要求,则加入队列
queue.append((i+1,j))
if i<m and j+1<n:#右边
queue.append((i,j+1))
return len(res)
if __name__ == '__main__':
m,n,k=2,3,1
s=Solution()
print(s.movingCount(m,n,k))#3
print(s.movingCount2(m,n,k))#3
动态规划和递归的区别,回溯就是递归嘛
递归是一种算法结构,回溯是一种算法思想。
回溯法是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,故称回溯法。回溯就是通过不同的尝试来生成问题的解,有点类似于穷举。
当回溯用于树的时候,就是深度优先搜索。当然了,几乎所有可以用回溯解决的问题都可以表示为树。那么这俩在这里就几乎同义了。如果一个问题解决的时候显式地使用了树,那么我们就叫它DFS
递归和动态编程能解决的问题都有一个特性:原问题(problem)可以分解成若干个子问题(sub-problem),只有先解决了子问题才能进一步解决原问题。子问题的解决方式形式上与原问题一致。
动态规划(DP)是通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法,动态规划常常适用于有重叠子问题和最优子结构性质的问题,
DP存储子问题的结果,当子问题已经被计算过,直接返回结果。因此,当需要重复计算子问题时,DP的时间效率高很多,但需要额外的空间。
递归的时间成本随递归深度n(单条路径中递归调用的次数)成指数增长;空间复杂度为O(n)。
动态编程的核心在于,如果在一个问题的解决方案中,子问题被重复计算,那么就可以利用记录中间结果,达到用空间换取时间的目的。
矩阵中的路径-剑指offer
请设计一个函数,用来判断在一个n乘m的矩阵中是否存在一条包含某长度为len的字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入盖格子。

思考:矩阵中每一个点我们都可以往他的四个方向查找,所以我们可以吧它想象为一颗4叉树,就是每个节点有4个子节点,而树的遍历我们最容易想到的就是递归
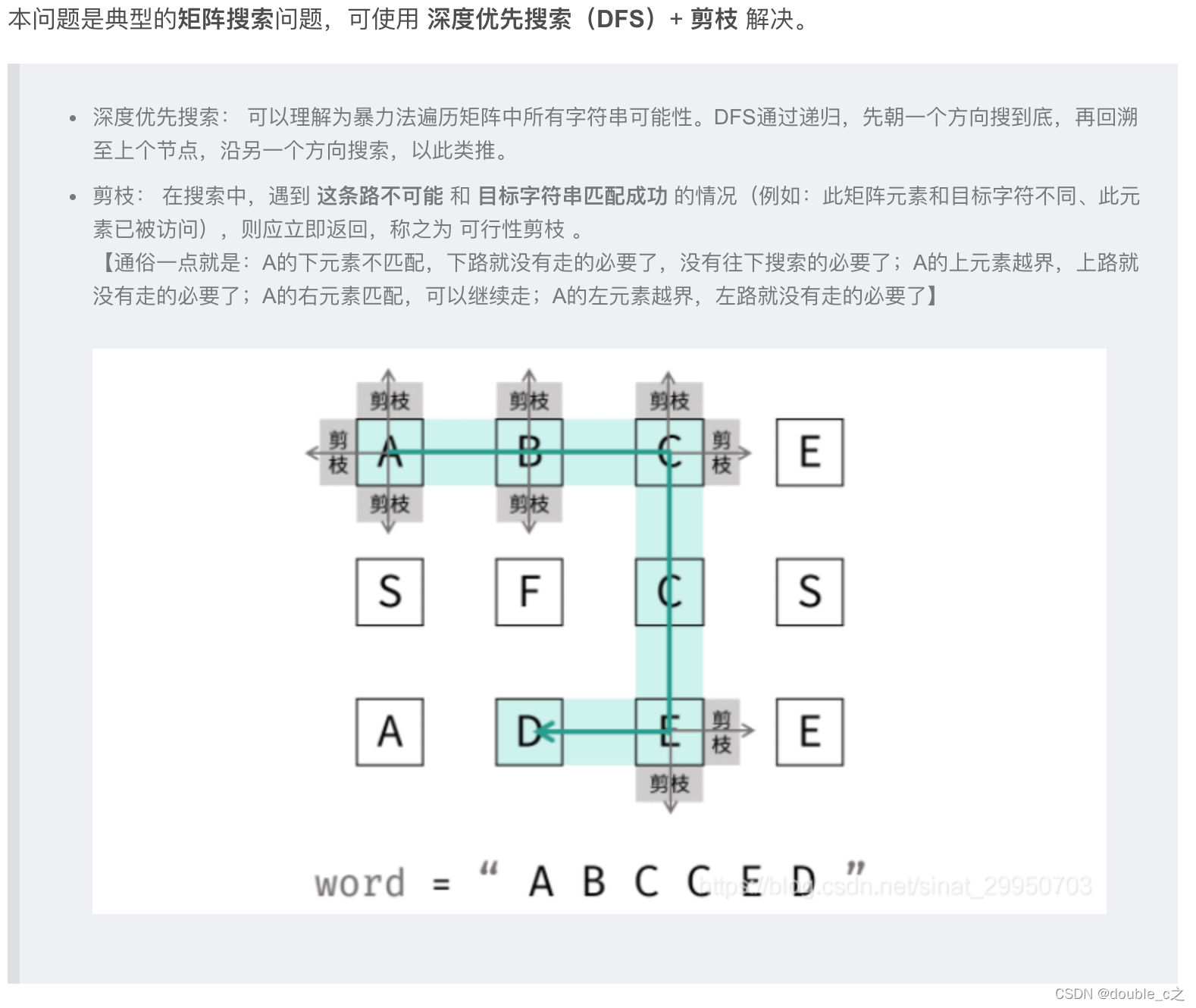
I.回溯法(递归):
思路:
首先矩阵中每一个字母都有可能是path的开头,因此遍历所有矩阵元素,只要有一次递归返回,则返回True;
递归思路:
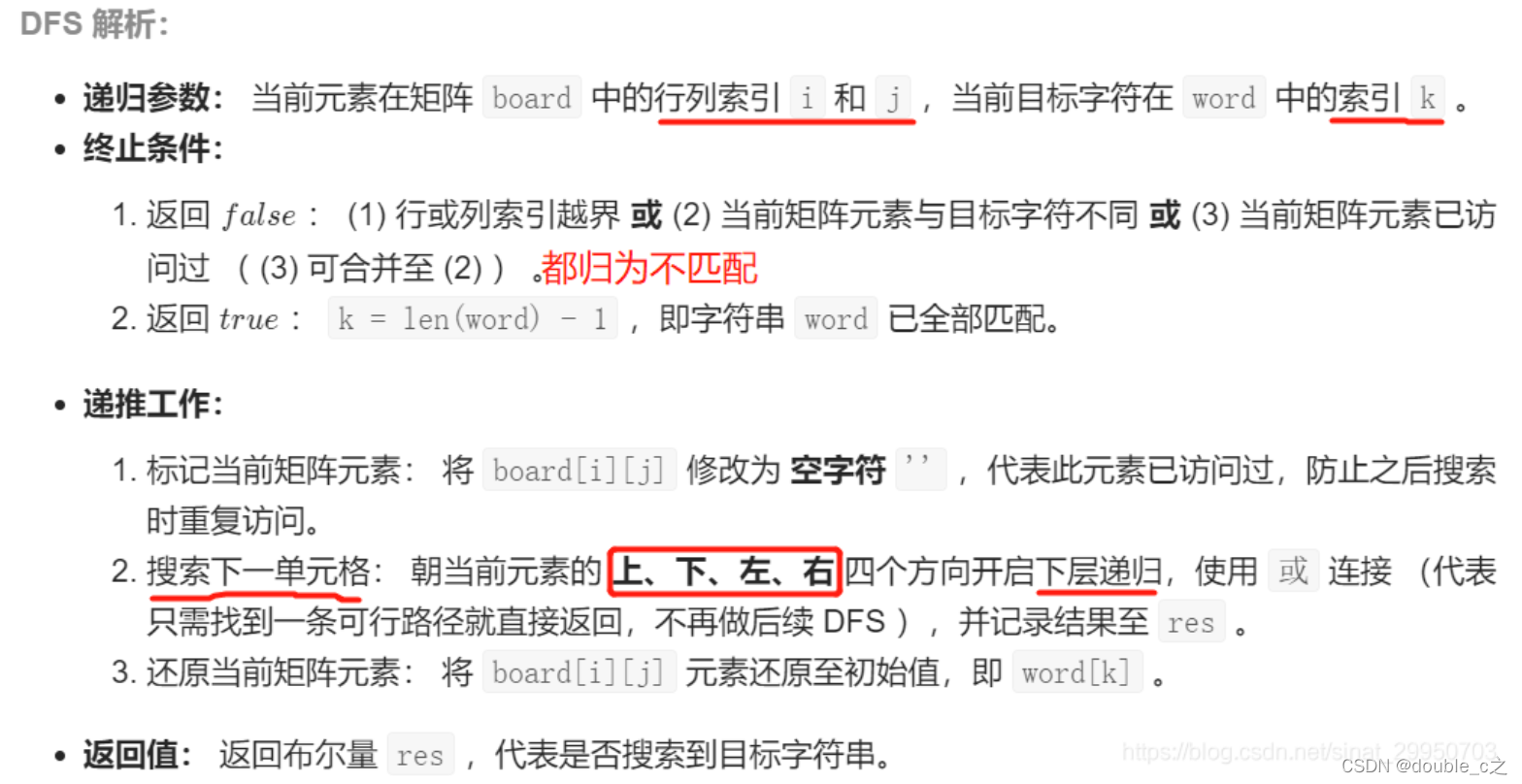
每一步递归做什么:给定当前matrix、当前位置r,c、当前path、和path中的第i个元素,判断从矩阵从(r,c)开始,path从第i个元素开始,两者是否匹配;
终止条件:
1.如果i==len(path),返回True,说明指针i指到了len(path)位置,说明path前面元素都匹配完毕
2.如果(r,c)越界了或者(r,c)位置已经被访问了,返回False;
3.如果(r,c)位置元素和path[i]不匹配,返回False
返回什么:
如果(r,c)和path[i]匹配成功,先更改matrix使得当前位置职位‘#’(已遍历)
(该更改后的matrix 会被直接传到下一轮递归),再判断下一位置是否匹配。下一位置有四种:上、下、左、右,使用or连接,只要有一个返回True就可以了
该方法和官方方法不同之处:不需要新建一个visted矩阵来记录遍历情况,直接在matrix上进行更改,并将改变好的matrix传入下一次递归。但是需要注意的地方在于第10行,因为矩阵的每个字母都有可能作为开头,因此遍历所有字母时,传入的matrix应该是同样干净的(没有被遍历过),因此使用了一个深拷贝(python3也可以使用copy方法)。
II.BFS广度优先遍历
思考:
递归的时候,需要不断向子递归函数传入当前已经遍历过的矩阵,矩阵检测位置(r,c+1)/(r,c-1)/(r+1,c)(r-1,c),还有path的检测位置(i+1)。这三者的存储也可以通过BFS来实现,设想一颗四叉树,每一个节点存储(当前遍历过的矩阵,矩阵检测位置,path检测位置),然后只要path的检测位置i移动到了最后,就返回True,否则继续建立新的子节点(四个方向)
这里需要注意的地方:第10行处的matrix和path必须是深拷贝,原因同上。(这里之所以path也深拷贝是因为没有使用指针i来遍历path,而是直接遍历一个pop一个,因此path是动态的,所以在初始化时要深拷贝)
还有在存储四个子节点时,cur_matrix和cur_path同样需要深度拷贝,因为两者都是动态的,有人可能会问为什么回溯法中调用子递归函数时不需要深度拷贝?那是因为递归函数在参数传入的过程就已经深度拷贝了。
因此无论哪种方法,必然都要遍历所有可能的路径,空间消耗也是一样的。
class Solution:
def hasPath(self, matrix, rows, cols, path):
if not path:
return False
# 给定的matrix是个字符串,将该字符串转变成真正的matrix
matrix = list(matrix)
path = list(path)
for i in range(rows):
for j in range(cols):
if self.BFS_search(matrix[:], i, j, rows, cols, path[:]):
return True
return False
def BFS_search(self, matrix, i, j, rows, cols, path):
queue = []
queue.append(((i,j), matrix, path))
while queue:
cur_pos, cur_matrix, cur_path = queue.pop(0)
if not cur_path:
return True
r = cur_pos[0]
c = cur_pos[1]
if 0<=r<rows and 0<=c<cols and cur_matrix[r*cols + c] != '#' and matrix[r*cols + c] == cur_path[0]:
cur_matrix[r*cols + c] = '#'
cur_path.pop(0)
queue.append(((r+1,c), cur_matrix[:], cur_path[:]))
queue.append(((r-1,c), cur_matrix[:], cur_path[:]))
queue.append(((r,c+1), cur_matrix[:], cur_path[:]))
queue.append(((r,c-1), cur_matrix[:], cur_path[:]))
return False
class Solution2:
def hasPath(self, matrix, rows, cols, path):
if not matrix or not path:
return False
matrix = list(matrix) #转换成list方便记录走过的位置
hasornot = False
for r in range(rows):
for c in range(cols):
if self.haspath(matrix[:], rows, cols, r, c, path, 0):
return True
return False
def haspath(self, matrix, rows, cols, r, c, path, i):
# 返回什么:返回matrix从(r,c)位置开始,path从i位置开始,两者是否匹配
if i==len(path):
return True
if not 0<=r<rows or not 0<=c<cols or matrix[r*cols + c] == '#':# 越界或者已经访问过了
return False
if matrix[r*cols + c] != path[i]: # 不匹配
return False
else: # 匹配
matrix[r*cols + c] = '#' # 将当前位置置为visited
#下一位置有四种:上、下、左、右,使用or连接,只要有一个返回True就可以了
return self.haspath(matrix, rows, cols, r, c+1, path, i+1) or \
self.haspath(matrix, rows, cols, r, c-1, path, i+1) or \
self.haspath(matrix, rows, cols, r+1, c, path, i+1) or \
self.haspath(matrix, rows, cols, r-1, c, path, i+1)
if __name__ == '__main__':
matrix="ABCESFCSADEE"
path="ABCCED"
rows=3
cols=4
s=Solution()
s2=Solution2()
print(s2.hasPath(matrix, rows, cols, path))
# print(s.hasPath(matrix, rows, cols, path))
