什么是深度优先搜索?
???深度优先搜索(DFS)属于图算法的一种,类似于树的前序遍历,是树的前序遍历的推广。过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。
??关于树的前序遍历可以参考上一篇博文:二叉树的遍历
深度优先搜索的过程
- 从图中某个顶点v出发,访问顶点v
- 找出刚访问过的顶点的第一个未被访问的邻接点,访问该顶点。以该顶点为新顶点,重复此步骤,直至刚访问过的顶点没有未被访问的邻接点为止。
- 返回前一个访问过的且仍有未被访问的邻接点的顶点,找出该顶点的下一个未被访问的邻接点,访问该顶点。
- 重复此步骤(2)和(3),直至图中所有顶点均被访问过,访问结束。
??用图表示一下:(蓝色实线表示访问下一个未被访问邻接点,红色虚线表示回溯,路线旁的数字表示访问的顺序)

??所以搜索结果为: v1 v2 v4 v8 v5 v3 v6 v7 (深度优先搜索的结果不是唯一的,因为每个邻接点大于1的节点在访问该节点的邻接点时的顺序不唯一)
深度优先搜索题目:
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
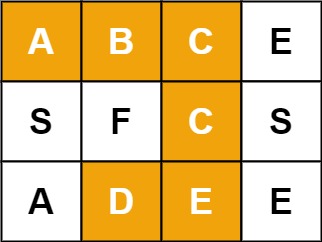
例如,在下面的 3×4 的矩阵中包含单词 “ABCCED”(单词中的字母已标出)。
示例 1:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" 输出:true示例 2:
输入:board = [["a","b"],["c","d"]], word = "abcd" 输出:false
? 这道题使用深度优先搜索,先朝一个方向搜到底,在回溯至上一个节点,选择另一条满足条件的路线,直至找出结果。
递归参数: 当前元素在board中的索引值 i 和 j ,当前目标字符在 word 中的索引 k。
终止条件:
? 1.返回false:行或列索引越界 或 当前矩阵元素与目标字符不同 或当前矩阵元素已经访问过。
? 2.返回true:k = word.length - 1, 表示字符串word全部匹配
递推工作:
? 1.声明一个和board数组同样空间大小的辅助数组,全部赋值为false,代表全部未被访问,用来判断当前矩阵元素是否被访问过,访问的时候改为true,当前层dfs结束回溯时改回false,防止不能回溯。
? 2.搜索下一单元格:朝当前元素的上或 右 或 下 或 左四个方向开始下层dfs,循环步骤 1。
返回值: 返回布尔值ans,代表是否搜索到目标字符串word。
代码实现:
var exist = function(board, word) {
let ans = false//结果初始化为false(如果遍历完整个矩阵都没有结果则返回该值)
const row = board.length//board的行
const col = board[0].length//board的列
const end = word.length-1//目标字符串的长度
//用来判断矩阵当前字符是否走过,开始时false表示每个格子都没有被访问过
const visited = new Array(row).fill(0).map(() => new Array(col).fill(false))
const ways = [[-1,0], [0,1], [1,0], [0,-1]]//向上右下左的路线
//判断i,j是否越界
const overBoarder = (i, j) => {
return i < 0 || i >= row || j<0 || j >= col
}
//深度优先搜索(递归循环)
const dfs = (i, j, k) => {
//1.确定是否找到答案(是否满足条件)
if(k > end || ans){
return
}
//2.是否终止
if(k === end){
return ans = true
}
//3.继续搜索
for(const way of ways){
//往哪走
let [si, sj] = way
const ni = i+si
const nj = j+sj
//判断当前所选择的字符是否越界,越界则跳过下边语句结束本次循环,选择另一条way
if(overBoarder(ni, nj)){
continue
}
//判断当前所选择的字符是否等于下一个目标字符串,不等于则结束本次循环,另选其他路径
if(board[ni][nj] !== word[k+1]){
continue
}
//判断当前所选择的字符是否被访问过,访问过则结束本次循环,另选其他路径
if(visited[ni][nj] == true){
continue
}
//此时所选择的字符符合所有条件,访问该字符,并把该字符在visited中的位置改为true
visited[ni][nj] = true
//从当前所选择的字符进行搜索,直至最后
dfs(ni, nj, k+1)
//这一步是当前层dfs结束时把对应的visited改回false,因为在回溯两次的时候,第一次回溯的那个值可能以后还会用到,如果为true,则影响回溯
visited[ni][nj] = false
}
}
outer: for(let i = 0; i < row ; i++){
for(let j = 0; j < col ; j++){
if(ans){
break outer;//outer是在跳出本层循环的时候也跳出外层循环,因为此时外层循环也没有再循环的必要了,目的是防止算法超出时间限制
}
if(board[i][j] == word[0]){
visited[i][j] = true //表示这个字符被访问过了
dfs(i, j, 0)
visited[i][j] = false//重置为false,
}
}
}
return ans
};