[数据结构与算法] KMP字符匹配算法详解

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> KMP字符匹配算法详解 -> 正文阅读

[数据结构与算法]KMP字符匹配算法详解

KMP算法中有很多抽象的点，需要自己将其理顺了才能理解该算法的奇妙之处。为防止自己以后忘记，今特地记录一下。

字符匹配——暴力破解

先来看看该算法解决一个什么问题。先定义两个字符串：

String haystack="qwertyuiop";
String needle="yui";

怎样获取子串needle在haystack中的起始索引位置？
首先可以采用暴力破解法，定义两个指针h和n，初始化分别指向haystack的索引0和needle的索引0；
在这里插入图片描述

比较指针h处的字符与n处的字符是否相等，如果相等，指针h和n分别向后移。
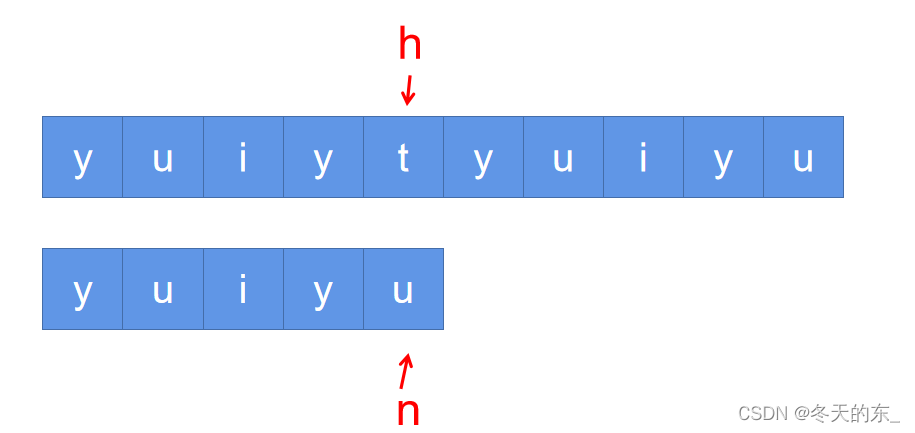
在这里插入图片描述

当两者所对应的字符不相等时，h回到初始位置的后一位置，n回到初始位置，然后重复上述的比较过程，直到n走完整个needle字符串或者h走完整个haystack字符串。

其实大家可以发现每次当h和n处的字符不匹配时，h和n都会回溯，采用上述暴力破解时，它们回溯的跨度是非常之大的，这就导致了搜索过程相当耗时。那么我们如果能解决h和n的回溯问题，其实就可以极大提高搜索效率，比如使h不再回溯到初始位置的下一位置，而是根据一定规则排除之前已经比较过的字符，回溯时直接回溯到这些字符的后面。对于n也是一样。
好了，至此我们知道了影响暴力破解法的搜索效率的罪魁祸首就是指针h和n的回溯。下面我们来看看KMP是如何干掉回溯问题的。

KMP

想要理解KMP算法，我们必须先来看一下另一个奇技淫巧：最长相等前后缀。在KMP中，这是相对于亚索e一样的存在（精髓），它直接关系到h和n回溯的位置。
最长相等前后缀也好理解，就是字面意思，指一个字符串中前缀和后缀相等时的最长字符串。比如“yuiyu”的最长相等前后缀为“yu”，“abcabca”为“a”。
这玩意虽然好理解，但是搭配起KMP那简直是直呼卧槽啊。让我捋一捋哈

我的眼睛望着窗外，幻想如何对你表白~。OK，捋顺了，咱们继续，下面有点高能。为了便于解释，先忘掉之前写的具体字符。在这里插入图片描述
刚才说了，每次h和n不匹配时，两者都会回溯，回溯到哪呢，现在是不知道的。不过没关系，我们先假设h回溯到h’的位置，并且最终成功完成了匹配，即其中haystack的灰色部分字符串和字符串needle完全匹配。
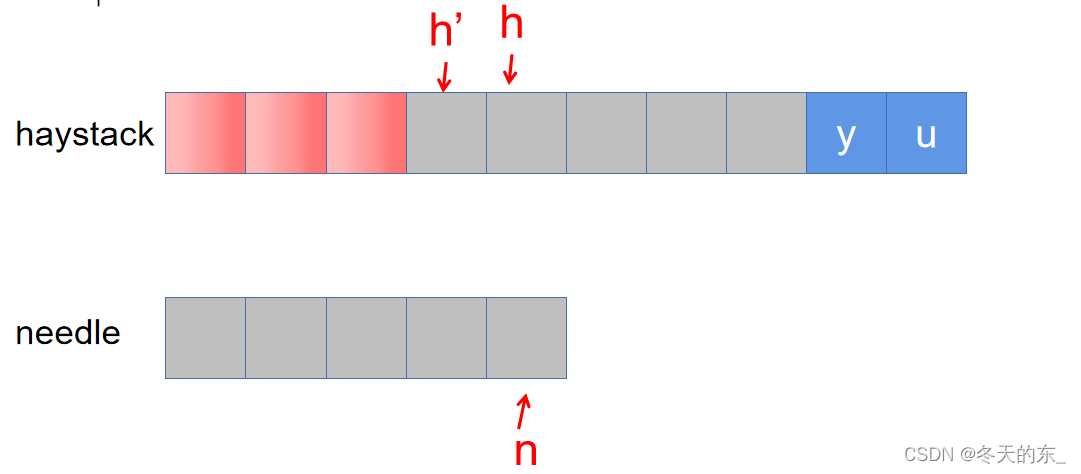
在这里插入图片描述
根据这个假设我们可以知道h’到h之间的字符串（假设有k个字符）一定是等于needle的前k个字符，即图中的黑色部分是相等的。

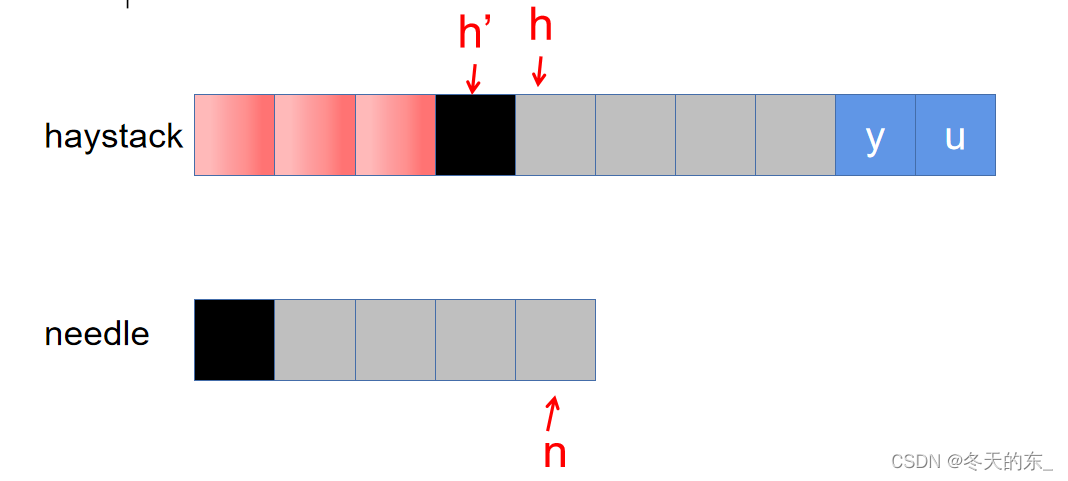
根据前面，我们是知道指针h前面的字符串和n前面的字符串s是相等的，所以黑色部分实际上就是字符串s的最长相等前后缀。因此我们回溯之前，只要知道指针n前面的字符串的最长相等前后缀的长度k就能确定指针n回溯到哪，也能确定h回溯到哪。实际上由于黑色部分相等，所以这之前的字符我们就没必要一一比较了，所以h不需要回溯，保持位置不变，而n调到needle的第k+1个字符的位置，然后再进行一一比较。如果再次出现不相等的情况，再次根据指针n前面的字符串的最长相等前后缀来确定回溯距离。
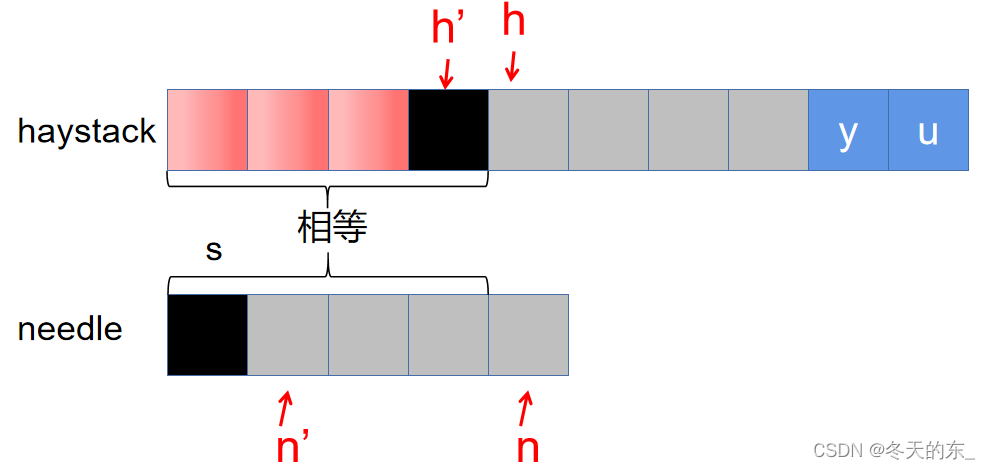
在这里插入图片描述
ok，利用最长相等前后缀来确定回溯的位置算是理解了。捋一下

首先移动指针h和n一一比较对应的字符是否相等，如果相等，h和n分别向后移；
如果不等，则根据在needle中指针n位置前面的字符串的最长相等前后缀来决定n的回溯位置n’，h保持不变。
比较h处的字符与n’处的字符是否相等，重复上述过程。

至于为啥根据needle中指针n位置前面的字符串的最长相等前后缀长度来决定n’的位置，刚刚已经说了，先假设回溯后找到了完全匹配的字符串，然后逆向来推。

OK，KMP算法已经解释完了，进行下一步。每一次比较的字符不相等时，我们都要去根据needle中指针n位置前面的字符串的最长相等前后缀长度来决定n’位置，所以需要事先获取到needle中每个索引i之前的最长相等前后缀长度。
先设定一个数组next[needle.length()]来存放我们想要的数据：其中next[i]表示needle中索引i之前（包括i）的字符串的最长相等前后缀的长度。

如何获取呢？假设已经知道n-1之前（包括n-1）的字符串的最长相等前后缀为黑色部分，是不是只需要判断n处和m处的字符是否相等就可以得到n（包括n）之前的字符串的最长相等前后缀了？如果相等则在黑色部分字符串的长度上+1就是当前的最长相等前后缀长度；如果不等则直接为0。是不是很好计算呀？
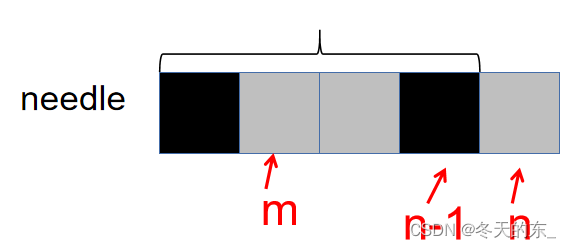
在这里插入图片描述
next获取到了后就可以根据它进行匹配了。
下面是匹配算法的代码，注意一些临界值的处理就ok啦。

public int strStr(String haystack, String needle) {

        int needleL = needle.length();

        //1.首先计算needle索引i之前（包括索引i）的字符串的最长相等前后缀长度。
        // next[i]表示索引i之前（包括索引i）的字符串的最长相等前后缀
        int[] next=new int[needleL];
        int k=0;//记录当前字符串的最长相等前后缀长度
        for (int i = 1; i < needleL; i++) {
            //如果当前字符（索引为i）与当前最长相等前后缀l1的后一字符不相等，
            // 则更新最长相等前后缀为l1的最长相等前后缀，
            // 直到最长相等前后缀长度为0或者当前字符与最长相等前后缀的后一字符相等。
            while(k>0&&needle.charAt(k)!=needle.charAt(i)){
                k=next[k-1];
            }
            //当前字符与最长相等前后缀的后一字符相等,则最长相等前后缀长度+1。
            if(needle.charAt(k)==needle.charAt(i)){
                k++;
            }
            //记录当前索引i之前（包括i）的字符串的最长相等前后缀长度
            next[i]=k;
        }
        //2.遍历haystack,寻找needle在haystack中的位置
        k=0;
        for (int i = 0; i < haystack.length(); i++) {
            while(k>0&&needle.charAt(k)!=haystack.charAt(i)){
                k=next[k-1];
            }
            if(needle.charAt(k)==haystack.charAt(i)){
                k++;
            }
            if(k==needleL){
                return i-k+1;
            }
        }
        return -1;
    }