两个操作:
push_up() 子节点的信息更新到父节点
push_down() 父节点信息下传到子节点 (懒标记)
线段树含有的基本操作
1.pushup(u)
2.build() 将一段区间初始化成线段树
3.modify() 修改 单点和区间
4.query() 查询某一段区间的内容
原理:除了最后一层之外是一颗满二叉树,用堆的方法来存储,一维数组存储整颗树。
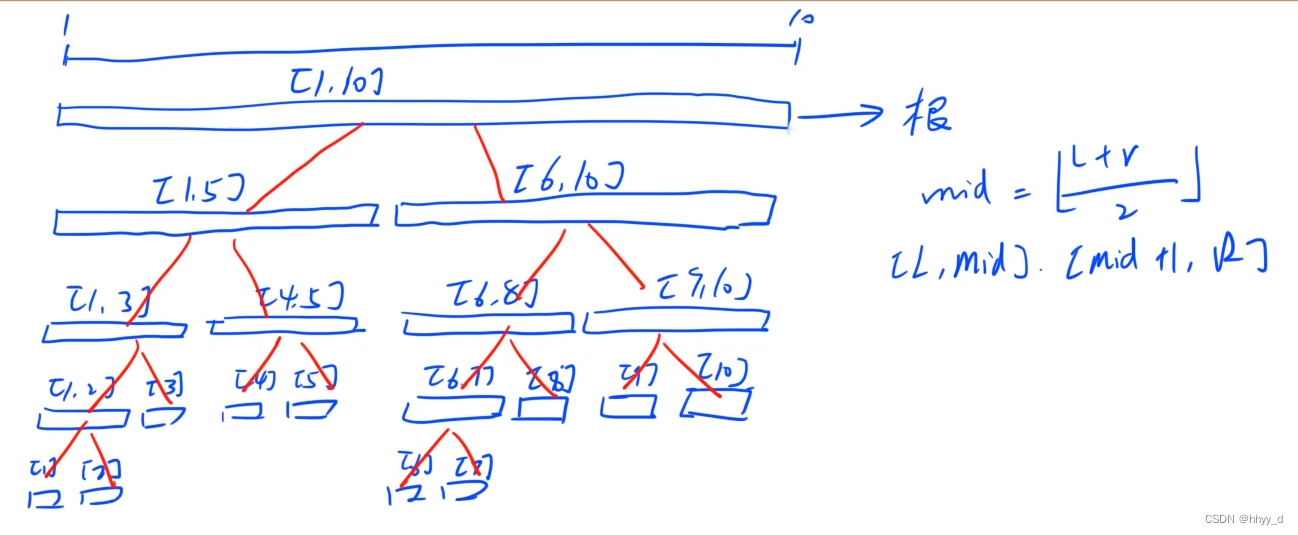

n个点的区间需要开4*n倍空间。
1、build函数
void build(int u,int l,int r)
{
tr[u].l l,tr[u].r = r;
if(l == r) return;
int mid = (l + r) >> 1;
build(u * 2,l,mid),build(u*2+1,mid+1,r);
pushup(u);
}
2、比如查询[5,9]的最大值,每个节点保存这个区间的最大值
[L,R] 表示查询的区间 [TL,TR]表示树中节点的位置
(1) [L,R] > [TL,TR] 直接返回 例如[3,5] [2,4]
(2) [L,R] & [TL,TR] 有交集,如果和左边有交集,递归到左边,和右边有交集,递归到右边。
(3) 没有交集不存在
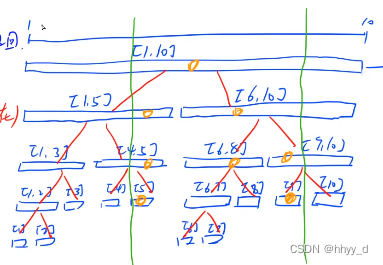
访问的节点数量一定是在log(n)的常数倍大小
例题:
1.最大数
可以看成是先生成n个位置,每次增加一个位置,就把对应位置上的数修改一下。 单点修改 区间查询
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 2e5+10;
struct Node
{
int l,r;
int v;
}tr[N*4];
int m,p;
void pushup(Node &u,Node &left,Node &right)
{
u.v = max(left.v,right.v);
}
void pushup(int u)
{
pushup(tr[u],tr[u*2],tr[u*2+1]);
}
void build(int u,int l,int r)
{
if(l == r) tr[u] = {l,r,0};
else
{
tr[u] = {l,r};
int mid = l + r >> 1;
build(u*2,l,mid),build(u*2+1,mid+1,r);
pushup(u);
}
}
Node query(int u,int l,int r)
{
if(tr[u].l >= l && tr[u].r <= r) return tr[u];
int mid = tr[u].l + tr[u].r >> 1;
if(r <= mid) return query(u*2,l,r);
else if(l > mid) return query(u*2+1,l,r);
else
{
auto left = query(u*2,l,r),right = query(u*2+1,l,r);
Node res;
pushup(res,left,right);
return res;
}
}
void modify(int u,int x,int v)
{
if(tr[u].l == x && tr[u].r == x) tr[u].v = v;
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid) modify(u*2,x,v);
else modify(u*2+1,x,v);
pushup(u);
}
}
int main()
{
cin >> m >> p;
build(1,1,m);
int last = 0,n = 0;
int x;
char op;
while(m --)
{
cin >> op >> x;
if(op == 'Q')
{
auto ans = query(1,n-x+1,n);
last = ans.v;
cout << last << "\n";
}
else
{
modify(1,n+1,((LL)x+last)%p);
n++;
}
}
return 0;
}
2.最大子段和
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 5e5+10;
int n,m;
int w[N];
struct Node
{
int l,r;
int tmax; //最大子段和
int sum; // 区间和
int lmax; //最大前缀和
int rmax; //最大后缀和
}tr[N*4];
void pushup(Node &u,Node &left,Node &right)
{
u.sum = left.sum + right.sum;
u.lmax = max(left.lmax,left.sum + right.lmax);
u.rmax = max(right.rmax,right.sum + left.rmax);
u.tmax = max(max(left.tmax,right.tmax),left.rmax+right.lmax);
}
void pushup(int u)
{
pushup(tr[u],tr[u*2],tr[u*2+1]);
}
void build(int u,int l,int r)
{
if(l == r)
{
tr[u] = {l,r,w[r],w[r],w[r],w[r]};
}
else
{
tr[u].l = l,tr[u].r = r;
int mid = l + r >> 1;
build(u*2,l,mid),build(u*2+1,mid+1,r);
pushup(u);
}
}
void modify(int u,int x,int v)
{
if(tr[u].l == x && tr[u].r == x) tr[u] = {x,x,v,v,v,v};
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid) modify(u*2,x,v);
else modify(u*2+1,x,v);
pushup(u);
}
}
Node query(int u,int l,int r)
{
if(tr[u].l >= l && tr[u].r <= r) return tr[u];
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(r <= mid) return query(u*2,l,r); // 全在左边
else if(l > mid) return query(u*2+1,l,r); // 全在右边
else
{
auto left = query(u*2,l,r),right = query(u*2+1,l,r);
Node res;
pushup(res,left,right);
return res;
}
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> w[i];
build(1,1,n);
while (m --)
{
int k,x,y;
cin >> k >> x >> y;
if(k == 1)
{
if(x > y) swap(x,y);
auto res = query(1,x,y);
cout << res.tmax << "\n";
}
else
{
modify(1,x,y);
}
}
return 0;
}
3.区间最大公约数
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 5e5+10;
LL n,m;
LL w[N];
struct Node
{
LL l,r;
LL v; //最大公约数
LL sum; // 区间和
}tr[N*4];
LL gcd(LL a,LL b)
{
return b ? gcd(b,a%b) : a;
}
void pushup(Node &u,Node &left,Node &right)
{
u.v = gcd(left.v,right.v);
u.sum = left.sum + right.sum;
}
void pushup(LL u)
{
pushup(tr[u],tr[u*2],tr[u*2+1]);
}
void build(LL u,LL l,LL r)
{
if(l == r)
{
LL b = w[r] - w[r-1];
tr[u] = {l,r,b,b};
}
else
{
tr[u].l = l,tr[u].r = r;
LL mid = l + r >> 1;
build(u*2,l,mid),build(u*2+1,mid+1,r);
pushup(u);
}
}
void modify(LL u,LL x,LL d)
{
if(tr[u].l == x && tr[u].r == x)
{
LL b = tr[u].sum + d;
tr[u] = {x,x,b,b};
}
else
{
LL mid = tr[u].l + tr[u].r >> 1;
if(x <= mid) modify(u*2,x,d);
else modify(u*2+1,x,d);
pushup(u);
}
}
Node query(LL u,LL l,LL r)
{
if(tr[u].l >= l && tr[u].r <= r) return tr[u];
else
{
LL mid = tr[u].l + tr[u].r >> 1;
if(r <= mid) return query(u*2,l,r);
else if(l > mid) return query(u*2+1,l,r);
else
{
auto left = query(u*2,l,r),right = query(u*2+1,l,r);
Node res;
pushup(res,left,right);
return res;
}
}
}
int main()
{
cin >> n >> m;
for (LL i = 1; i <= n; i ++ ) cin >> w[i];
build(1,1,n);
string op;
LL l,r,d;
while (m -- )
{
cin >> op >> l >> r;
if(op[0] == 'Q')
{
//cout << "yes" << endl;
auto left = query(1,1,l);
Node right({0,0,0,0});
if(l + 1 <= r) right = query(1,l+1,r);
LL ans = abs(gcd(left.sum,right.v));
cout << ans << "\n";
}
else
{
cin >> d;
modify(1,l,d);
if(r+1 <= n) modify(1,r+1,-d);
}
}
return 0;
}
