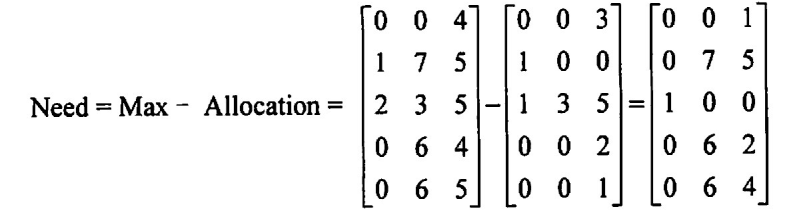安全序列
如果系统按照这种序列分配资源,则每个进程都能顺利完成。只要能找出一个安全序列,系统就是安全状态。
当然,安全序列可能有多个。
通俗理解模型
此时你是一位成功的银行家,手里有100亿资金…
此时有三个企业想找你贷款,分别是企业B,企业A,企业T
B:“大哥,我最多要借70亿”
A:“大哥,我最多要借40亿”
T:“大哥,我最多要借50亿”
有个规矩:借给企业的钱达不到企业提出的最大要求,那么你借的钱就打水漂了
当然你也不想你的钱打水漂,那么就要考虑 怎么借才能保证自己的100亿不打水漂
初始借完钱
| 最大要求 | 已经借走 | 最多再借 | |
|---|---|---|---|
| B | 70 | 20 | 50 |
| A | 40 | 10 | 30 |
| T | 50 | 30 | 20 |
此时你手里还有40亿…
分析借钱的安全序列
-
此时B想跟你借30亿,你敢借吗?
-
假如你答应了:借给了B 30亿,
那么你的手里还有10亿,上面的图稍作修改,如下图: -
最大要求 已经借走 最多再借 B 70 20 +30=5050 -30=20A 40 10 30T 50 30 20 -
如果其他企业再提出借20亿,那你巴比Q了,显然你借不了,你的钱打水漂了,所以这个钱不能借。
不安全
-
-
此时A想跟你借20亿,你敢借吗?
-
假如你答应了:借给了A 20亿,
那么你的手里还有20亿,上面的图稍作修改,如下图: -
最大要求 已经借走 最多再借 B 70 20 50A 40 10 +20=3030-20=10T 50 30 20 -
接下来你可以把这20亿都借给T企业。等他把钱全部还回来了,手里就有50亿,再把这些钱借给B企业。等他把钱全部还回来了,手里就有70亿,最后再借给A企业。这样你的钱就全回来了。
-
所以此借钱序列(安全序列):T->B->A
-
根据上述思路自行验证这个序列:A->T->B
-
银行家算法
核心思想
在进程提出资源申请时, 先预判此次分配是否会导致系统进入不安全状态。 如果会进入不安全状态, 就暂时不答应这次请求, 让该进程先阻塞等待。
核心是:安全性算法
资源表示
把单维的数字拓展为多维的向量。 比如: 系统中有5个进程 P0~P4, 3种资源 R0~R2, 初始数量为 (10, 5, 7)
| 进程 | 最大需求 | 已经分配 | 最多需要 |
|---|---|---|---|
| P0 | (7,5,3) | (0,1,0) | (7,4,3) |
| P1 | (3,2,2) | (2,0,0) | (1,2,2) |
| P2 | (9,0,2) | (3,0,2) | (6,0,0) |
| P3 | (2,2,2) | (2,1,1) | (0,1,1) |
| P4 | (4,3,3) | (0,0,2) | (4,3,1) |
此时已经分配了(7,2,5),还剩余(3,3,2)
安全性算法分析系统状态
-
此时系统是否处于一种安全状态?若是,则找出一条安全序列。
-
首先,检查剩余的资源是否满足各个进程的需求
-
我们发现能满足P1、P3的需求。那先分配给P1(将P1加入安全序列),等待他结束,那么剩余资源将变为(5,3,2);再分配给P3(将P3加入安全序列),等他结束,剩余资源将变为(7,4,3)。如下图:
-
进程 最大需求 已经分配 最多需要 P0 (7,5,3) (0,1,0) (7,4,3)P2 (9,0,2) (3,0,2) (6,0,0)P4 (4,3,3) (0,0,2) (4,3,1) -
将P4、P2、P0(他们最多需要的资源数小于剩余资源)加入安全序列,最终可得到一个安全序列。
安全性算法
-
-
实际做题(手算)的情况下可用更快速的方法找到一个安全序列
- (3, 3, 2) 可满足 P1、 P3, 说明无论如何, 这两个进程的资源需求一定是可以依次被满足的, 因此P1、 P3 一定可以顺利的执行完, 并归还资源。 可把 P1、 P3 先加入安全序列。(2, 0, 0) + (2, 1, 1) + (3, 3, 2) = (7, 4, 3)
剩下的 P0、 P2、 P4 都可被满足。 同理, 这些进程都可以加入安全序列 。于是, 5个进程全部加入安全序列, 说明此时系统处于安全状态, 暂不可能发生死锁。
- (3, 3, 2) 可满足 P1、 P3, 说明无论如何, 这两个进程的资源需求一定是可以依次被满足的, 因此P1、 P3 一定可以顺利的执行完, 并归还资源。 可把 P1、 P3 先加入安全序列。(2, 0, 0) + (2, 1, 1) + (3, 3, 2) = (7, 4, 3)
-
特殊:找不到安全序列的列子
-
进程 最大需求 已经分配 最多需要 P0 (8, 5, 3) (0, 1, 0) (8, 4, 3)P1 (3,2,2) (2,0,0) (1,2,2)P2 (9, 5 ,2) (3, 0, 2) (6, 5, 0)P3 (2,2,2) (2,1,1) (0,1,1)P4 (4, 3, 6) (0, 0, 2) (4, 3, 4) -
资源总数(10,5,7),剩余可用资源(3,3,2)
-
(3, 3, 2) 可满足 P1、 P3,可把 P1、 P3 先加入安全序列,剩余可用资源(7, 4, 3)
-
进程 最大需求 已分配 最多还需要 P0 (8, 5, 3) (0, 1, 0) (8, 4, 3)P2 (9, 5 ,2) (3, 0, 2) (6, 5, 0)P4 (4, 3, 6) (0, 0, 2) (4, 3, 4) -
剩下的无法满足,每一位对比。剩下的 P0 需要 (8, 4, 3)
(7, 4, 3)P2 需要 (6, 5, 0)(7, 4, 3)P4 需要 (4, 3, 4) -
无法找到任何一个安全序列, 说明
此时系统处于不安全状态, 有可能发生死锁
-
下面进入正题:银行家算法的实现
银行家算法实现
| 进程 | 最大需求Max | 已分配Allocation | 最多还需要Need |
|---|---|---|---|
| P0 | (7, 5, 3) | (0, 1, 0) | (7, 4, 3) |
| P1 | (3, 2, 2) | (2, 0, 0) | (1, 2, 2) |
| P2 | (9, 0 ,2) | (3, 0, 2) | (6, 0, 0) |
| P3 | (2, 2, 2) | (2, 1, 1) | (0, 1, 1) |
| P4 | (4, 3, 3) | (0, 0, 2) | (4, 3, 1 |
数据结构:
n*m 矩阵 Max 表示各进程对资源的最大需求数
n*m 矩阵 Allocation 表示已经给各进程分配 了多少资源
Max – Allocation = Need 矩阵表示各进程最多还需要多少资源
长度为 m 的一维数组 Available 表示还有多少可用资源 [表示:Available = (3, 3, 2)]
用长度为 m 的一位数组 Requesti表示进程此次申请的各种资源数 [表示:Request0 = (2, 1, 1) ]
思路分析
-
如果 Requesti[j]≤Need[i, j] (0≤j≤m)便转向
2; 否则认为出错 :因为它所需要的资源数已超过它所宣布的最大值 -
如果 Requesti[j]≤Available[j] (0≤j≤m), 便转向
3; 否则表示尚无足够资源, Pi必须等待 -
系统试探着把资源分配给进程Pi, 并修改相应的数据(
并非真的分配, 修改数值只是为了做预判)Available = Available - Requesti; Allocation[i, j] = Allocation[i, j] + Requesti[j]; Need[i, j] = Need[i, j] – Requesti[j] -
操作系统执行
安全性算法, 检查此次资源分配后,系统是否处于安全状态。 若安全, 才正式分配; 否则, 恢复相
应数据, 让进程阻塞等待
银行家算法步骤
- 检查此次申请是否超过了之前声明的最大需求数
- 检查此时系统剩余的可用资源是否还能满足这次请求\
- 试探着分配, 更改各数据结构
- 用安全性算法检查此次分配是否会导致系统进入不安全状态
安全性算法步骤
检查当前的剩余可用资源是否能满足某个进程的最大需求, 如果可以, 就把该进程加入安全序列,并把该进程持有的资源全部回收。
不断重复上述过程, 看最终是否能让所有进程都加入安全序列。
系统处于不安全状态未必死锁, 但死锁时一定处于不安全状态。 系统处于安全状态一定不会死锁
升华思维
死锁预防是保证系统不进入死锁状态的静态策略,其解决办法是破坏产生死锁的四个必要条件之一、下列方法中 破坏了“循环等待”条件的是( )。
A. 银行家算法
B. 一-次性分配策略
C. 剥夺资源法
D. 资源有序分配策略
产生死锁的四个必要条件:互斥、不剥夺、请求和保持、循环等待
资源有序分配策略可以限制循环等待条件的发生。选项A判断是否为不安全状态;选项B破坏了占有请求条件;选项C破坏了非剥夺条件。
某系统中有三个并发进程都需要四个同类资源,则该系统必然不会发生死锁的最少资源是( )。
A. 9
B. 10
C. 11
D. 12
资源数为9时,存在三个进程都占有三个资源,为死锁;资源数为10 时,必然存在一个进程能拿到4个资源,然后可以顺利执行完其他进程。
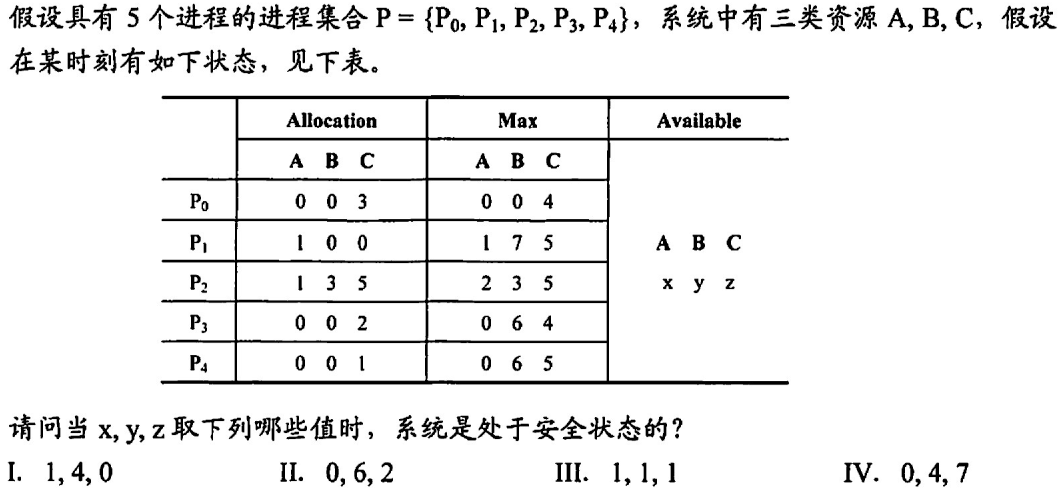
A. Ⅱ、Ⅲ
B. Ⅰ、Ⅱ
C. Ⅰ
D. Ⅰ、Ⅲ