A

点击此处查看对应的题目.
本题设计算法：模拟
开一个map，统计每个数字的出现次数即可

时间复杂度 $O (n)$

#include <iostream>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;

int main()
{
    map<char,int> m;
    string s;
    cin >> s;
    for (int i = 0;i < s.size();i ++ ) {
        m[s[i]] ++;
    }
    for (char i = '0';i <= '9';i ++ ) {
        if (!m[i]) {
            cout << i << '\n';
            break;
        }
    }
    return 0;
}

B

点击此处查看对应的题目.
本题设计算法：模拟

按照题意模拟一下整个过程即可

时间复杂度 $O (l o g k)$

#include <iostream>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;
typedef long long ll;

int main()
{
    ll a,b,k;
    cin >> a >> b >> k;
    ll res = 0;
    while (a < b) {
        a *= k;
        res ++;
    }
    cout << res << '\n';
    return 0;
}

C

点击此处查看对应的题目.
本题设计算法：动态规划

本题的题意就是构造得到一个满足下面条件的序列的方案数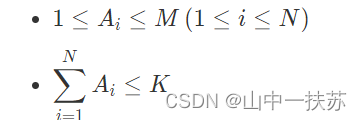请添加图片描述
那么，我们就可以发现这就类似背包问题

状态表示：我们可以用 dp(i,j)数组，表示在构造生成的序列中前 i 个字符中，元素值的总和为 j 的所有方案数

状态转移：枚举每个元素的每种取值可能
dp[i][k] = (dp[i][k] + dp[i - 1][k - j]) % mod;

时间复杂度 $O (n ? m ? k)$

#include <iostream>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;
typedef long long ll;
const int N = 110,M = 10010;
ll n,m,K,res;
ll mod = 998244353;
ll dp[N][M];

int main()
{
    cin >> n >> m >> K;

    dp[0][0] = 1;
    for(int i = 1;i <= n;i ++)
        for(int j = 1;j <= m;j ++)
            for(int k = i + j - 1;k <= K;k ++)
                dp[i][k] = (dp[i][k] + dp[i - 1][k - j]) % mod;

    for (int i = n;i <= K;i ++ ) res = (res + dp[n][i]) % mod;//总和数最低为n，所以累加答案的时候
    cout << res << '\n';
    return 0;
}

D

点击此处查看对应的题目.
本题设计算法：二分查找

本题要查找每个值的区间范围中 x 的个数，所以我们可以先将每个值的出现的下标用邻接表的形式统计一下，以便于缩小查找区间，然后再进行查找 x 的操作。

然而，本题查找 x 的次数极多，所以查找要用二分查找的方式进行。

时间复杂度 $O (q l o g n)$

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int N = 2e5 + 10;
int a[N];
vector<int> idx[N];

int main() {
    int n;
    cin >> n;
    for (int i = 1;i <= n;i ++ ) {
        cin >> a[i];
        idx[a[i]].push_back(i);
    }
    int q;
    cin >> q;
    while (q -- ) {
        int l,r,x;
        cin >> l >> r >> x;

        int lidx = lower_bound(idx[x].begin(),idx[x].end(),l) - idx[x].begin();
        int ridx = upper_bound(idx[x].begin(),idx[x].end(),r) - idx[x].begin();
        cout << ridx - lidx << '\n';
    }

    return 0;
}

E

点击此处查看对应的题目.
本题设计算法：计算几何 + 离散化

本题的题意：

给出直角坐标系上N个点(N <= 300)，求经过这些点中至少K个点的直线数量，若有无穷多条，则输出"Infinity"。

本题思路：

如果枚举点来找直线的话，复杂度过大，所以我们可以将点两两离散化出来成为直线（因为两点确定一条直线）
当K==1时，答案自然是无穷多条。
当K >= 2时，我们可以枚举两点，求出其确定的直线，再枚举所有点，判断该直线经过的点数是否不少于K。

求直线方程：

用直线的方程 y = kx + b 来表示直线，但由于 k 是 dy / dx，这里最开始我是用浮点数来表示，但问题是浮点数的误差比较大所以咱们可以将 y = kx + b 变形 y = (dy / dx) * x 然后再变形 y * dx = dy * x + b * dx。
已知经过点（x1，y1），（x2，y2），那么dy = y2 - y1, dx = x1 - x2, dxb = y * dx- dy *.x。
为了方便直线的判重，对参数进行处理（唯一性），使得：dy,dx,dxb三数公因数为1，(dx < 0 || (dx == 0 && dy < 0))

时间复杂度 $O(n ^ 3)$

#include <iostream>
#include <set>
#include <algorithm>
#include <set>
#include <array>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N = 1010,INF = 1e9 + 7;
PII point[N];
#define x first
#define y second

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}
int main()
{
    int n,k;
    cin >> n >> k;
    for (int i = 1;i <= n;i ++ ) cin >> point[i].x >> point[i].y;
    if (k == 1) {
        puts("Infinity");
        return 0;
    }

    set<array<int,3>> s;
    for (int i = 1;i < n;i ++ ) {
        for (int j = i + 1;j <= n;j ++ ) {
            int dy = point[i].y - point[j].y,dx = point[i].x - point[j].x;

            int d = gcd(abs(dy),abs(dx));
            dx /= d,dy /= d;
            if(dx < 0 || (dx == 0 && dy < 0)) dx = -dx,dy = -dy;
            int dxb = point[i].y * dx- dy * point[i].x;
            if(s.count({dx,dy,dxb})) continue;//防止完全相同的情况

            int cnt = 0;
            for (int t = 1; t <= n; t ++) {
                if (dy * point[t].x + dxb == dx * point[t].y)
                    cnt++;
            }
            if (cnt >= k) s.insert({dx,dy,dxb});
        }
    }

    cout << s.size() << '\n';
    return 0;
}

}