P2257 YY的GCD

https://www.luogu.com.cn/problem/P2257

重学莫反*2.
第一眼看过去， “这不是莫反sb题”，直接搞了个代码，然后T了:).
算了下时间复杂度，我敲，发现这东西不好搞。通过自己的努力，搞了一下午，终于忍不住去看了题解。发现确实妙啊。

暴力特别好搞。
让我们随便推一下暴力的公式。

$∑_i^n∑_j^m[gcd(i , j) == primes] \\ ∑_{p \in primes}∑_i^n∑_j^m[gcd(i , j) == p] \\$
这个比较眼熟：
$_i^n∑_j^m[gcd(i , j) == p]$
可以直接搞成:
$∑_d^{n/p}μ(d)*[\frac{n}{pd}] *[\frac{m}{pd}]$

所以暴力可以搞成：
$∑_{p \in primes}∑_d^nμ(d)*[\frac{n}{pd}] *[\frac{m}{pd}]$
可以大致算一下。素数的个数大概少一个数量级。那么时间复杂度为：
$\sqrt n)))$
这个复杂度，会很愉快的T掉。

通过我的挣扎去翻的题解。发现了一个自己~~曾经会的东西~~ 。但是我想用通俗的东西去解释，发现还不好解释，就一直很不愉悦。

但是我还是想通俗的解释一下：首先，通过暴力，我们实际上是在算每一个 $p r i m e s$ ,所对应的 $g c d (i, j) = p r i m e s$ ,而且计算 $g c d (i, j)$ 的过程，相当于枚举每一个 $p r i m e s$ 的倍数，也就是 $p d$ ,但是我们可以换一种枚举方式，直接枚举每一个数，去看每一个 $p d$ 的因子是质数的因子有多少个，而对于这个问题，可以预处理出来。
(懒得打公式，直接贴了个洛谷的图片)
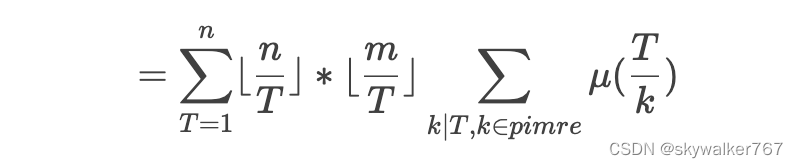
在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;

#define endl '\n'
#define pb push_back
#define mp make_pair
#define PI acos(-1)
#define lowbit(x) (x & (-x))
#define sz(x) ((int)(x).size())
#define all(a) a.begin() , a.end()
#define rn(i , n) for (int i = 0;i < (n); ++ i)
#define rep(i, a, b) for (int i = (a); i <= (b); ++i)
#define pre(i, b, a) for (int i = (b); i >= (a); --i)
#define debug(x) cout << #x << ": " << x << endl

typedef long long LL;
typedef long double db;
typedef vector<int> VI;
typedef pair<int , int > PII;

const int INF = 0x3f3f3f3f;
const LL MOD = 1000000007;
mt19937 mrand(random_device{}()); 
int rnd(int x) { return mrand() % x;}
LL gcd(LL a, LL b) { return b?gcd(b,a%b):a;}
LL _power(LL a , LL b) {LL res=1 % MOD;a%=MOD; assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%MOD;a=a*a%MOD;}return res;}
const int N = 1e7;
int tot , mu[N + 10] , pr[N / 5] , p[N + 10] , _;
LL sum[N + 10], f[N + 10];
void init(int n)
{
	mu[1] = 1;
	for (int i = 2;i <= n;i ++ ){
		if (!p[i]) p[i] = i , pr[++ tot] = i , mu[i] = -1;
		for (int j = 1;j <= tot && pr[j] * i <= n;j ++ ){
			p[pr[j] * i] = pr[j];
			if (pr[j] == p[i]) break;
			mu[i * pr[j]] -= mu[i];
		}
	}
	for (int i = 1;i <= tot;i ++)
	{
		for (int j = 1;j * pr[i] <= n;j ++){
			f[j * pr[i]] += mu[j];
		}
	}
	// rep(i , 1 , n) mu[i] += mu[i - 1];
	for (int i = 1;i <= n;i ++) sum[i] = sum[i - 1] + f[i];
}

void solve()
{
	int n , m;
	scanf("%d %d" , &n , &m);
	if (n > m) swap(n , m);
	LL ans = 0;
	for (int l =  1 , r;l <= n;l = r + 1){
		r = min(n / (n / l) , m / (m / l));
		ans = ans + 1LL * (n / l) * (m / l) * (sum[r] - sum[l - 1]);
	}
	printf("%lld\n" , ans);
}


int main()
{
	init(1e7);	
	for (scanf("%d" , &_);_;_ --) {
		solve();
	}
	return 0; 
}