一、知识准备
**首先是堆的概念。**这里的堆其实可以简单的理解成金字塔形的形象体。我们用二叉树来构造,但是我们这个二叉树是完全体,也就是树的扩展是要有顺序排列的。
- 堆是一个完全二叉树。
- 完全二叉树: 二叉树除开最后一层,其他层结点数都达到最大,最后一层的所有结点都集中在左边(左边结点排列满的情况下,右边才能缺失结点)。
- 大顶堆:根结点为最大值,每个结点的值大于或等于其孩子结点的值。
- 小顶堆:根结点为最小值,每个结点的值小于或等于其孩子结点的值。
- 堆的存储: 堆由数组来实现,相当于对二叉树做层序遍历。
大堆顶:
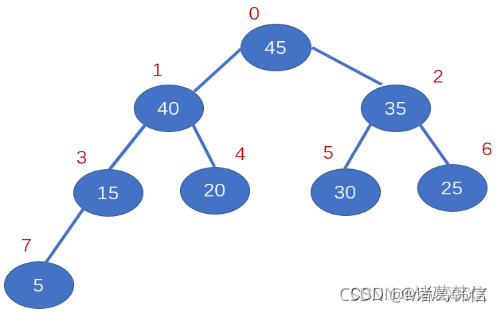
小堆顶:
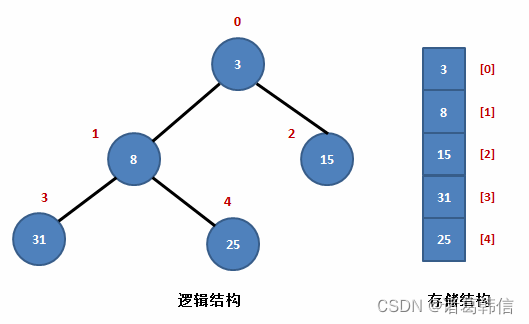
二、排序思路
- 将初始二叉树转化为大顶堆(heapify)(实质是从第一个非叶子结点开始,从下至上,从右至左,对每一个非叶子结点做heapify操作),此时根结点为最大值,将其与最后一个结点交换。
- 除开最后一个结点,将其余节点组成的新堆转化为大顶堆(实质上是对根节点做heapify操作),此时根结点为次最大值,将其与最后一个结点交换。
- 重复步骤2,直到堆中元素个数为1(或其对应数组的长度为1),排序完成。
三、动图演示
动图1:

动图2:

四、JS代码实现
**// 交换两个节点
function swap(A, i, j) {
let temp = A[i];
A[i] = A[j];
A[j] = temp;
}
// 将 i 结点以下的堆整理为大顶堆,注意这一步实现的基础实际上是:
// 假设 结点 i 以下的子堆已经是一个大顶堆,shiftDown函数实现的
// 功能是实际上是:找到 结点 i 在包括结点 i 的堆中的正确位置。后面
// 将写一个 for 循环,从第一个非叶子结点开始,对每一个非叶子结点
// 都执行 shiftDown操作,所以就满足了结点 i 以下的子堆已经是一大
//顶堆
function shiftDown(A, i, length) {
let temp = A[i]; // 当前父节点
// j<length 的目的是对结点 i 以下的结点全部做顺序调整
for(let j = 2*i+1; j < length; j = 2*j+1) {
temp = A[i]; // 将 A[i] 取出,整个过程相当于找到 A[i] 应处于的位置
if(j+1 < length && A[j] < A[j+1]) {
j++; // 找到两个孩子中较大的一个,再与父节点比较
}
if(temp < A[j]) {
swap(A, i, j) // 如果父节点小于子节点:交换;否则跳出
i = j; // 交换后,temp 的下标变为 j
} else {
break;
}
}
}
// 堆排序
function heapSort(A) {
// 初始化大顶堆,从第一个非叶子结点开始
for(let i = Math.floor(A.length/2-1); i >= 0; i--) {
shiftDown(A, i, A.length);
}
// 排序,每一次for循环找出一个当前最大值,数组长度减一
for(let i = Math.floor(A.length-1); i > 0; i--) {
swap(A, 0, i); // 根节点与最后一个节点交换
shiftDown(A, 0, i); // 从根节点开始调整,并且最后一个结点已经为当
// 前最大值,不需要再参与比较,所以第三个参数
// 为 i,即比较到最后一个结点前一个即可
}
}
let Arr = [3, 6, 13, 8, 2];
heapSort(Arr);
console.log(Arr); // [2, 3, 6, 8, 13]
代码看起来比较复杂。其实我们只需要记住两大点:
1、堆排序面对的数组一开始是无序状态的,这个时候,我们需要构建一个规则中的排序顶(所有中的最大值或者最小值);那么就是代码中需要做的第一次循环,如下:
// 初始化大顶堆,从第一个非叶子结点开始
for(let i = Math.floor(A.length/2-1); i >= 0; i--) {
shiftDown(A, i, A.length);
}
循环完成,我们就可以得到如下的数据:
[13, 8, 3, 6, 2]
上边的数就是我们循环第一次后的数据,可以知道,把他们依次放入完全体的二叉树中,父节点始终是最大的那个。
那么接下来我们只需要继续循环下去。
2、通过头一次的循环,整个完全二叉树已经构造,但是数据还没有排序完成,我们需要做的就是把这个二叉树,重复方法一,进行排序。所以才会有第二轮的循环,如下:
// 排序,每一次for循环找出一个当前最大值,数组长度减一
for(let i = Math.floor(A.length-1); i > 0; i--) {
swap(A, 0, i); // 根节点与最后一个节点交换
shiftDown(A, 0, i); // 从根节点开始调整,并且最后一个结点已经为当
// 前最大值,不需要再参与比较,所以第三个参数
// 为 i,即比较到最后一个结点前一个即可
}
五、辅助理解案例
步骤1
初始化大顶堆,首先选取最后一个非叶子结点(我们只需要调整父节点和孩子节点之间的大小关系,叶子结点之间的大小关系无需调整)。设数组为arr,则第一个非叶子结点的下标为:i = Math.floor(arr.length/2 - 1) = 1,也就是数字4,如图中虚线框,找到三个数字的最大值,与父节点交换。
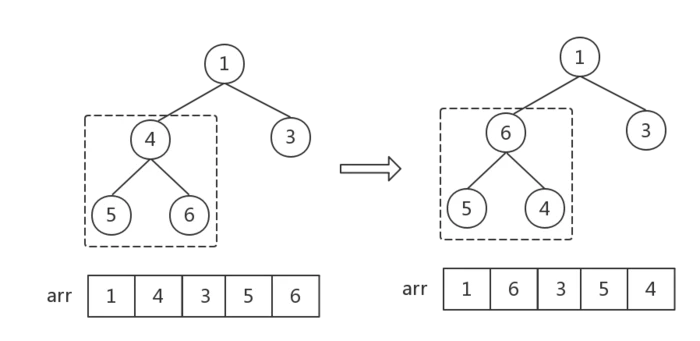
然后,下标 i 依次减1(即从第一个非叶子结点开始,从右至左,从下至上遍历所有非叶子节点)。后面的每一次调整都是如此:找到父子结点中的最大值,做交换。
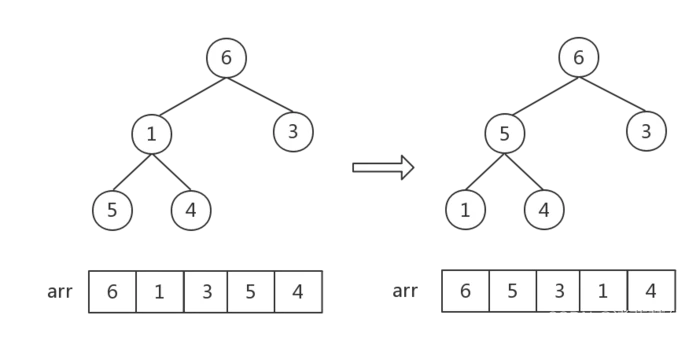
这一步中数字6、1交换后,数字[1,5,4]组成的堆顺序不对,需要执行一步调整。因此需要注意,每一次对一个非叶子结点做调整后,都要观察是否会影响子堆顺序!
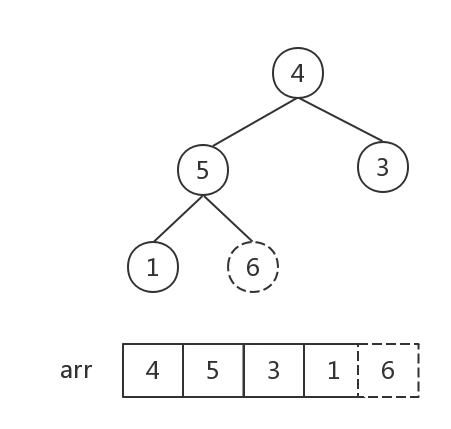
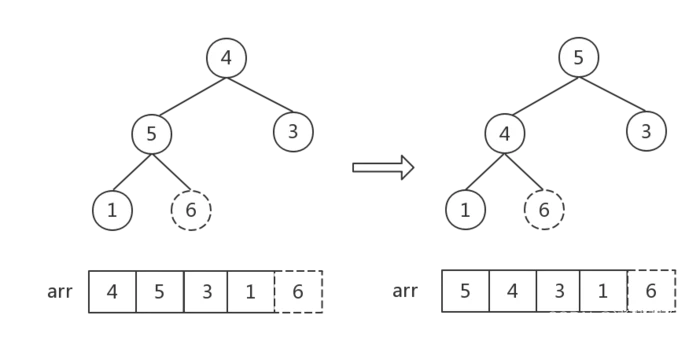
这次调整后,根节点为最大值,形成了一个大顶堆,将根节点与最后一个结点交换。
步骤二
除开当前最后一个结点6(即最大值),将其余结点[4,5,3,1]组成新堆转化为大顶堆(注意观察,此时根节点以外的其他结点,都满足大顶堆的特征,所以可以从根节点4开始调整,即找到4应该处于的位置即可)。
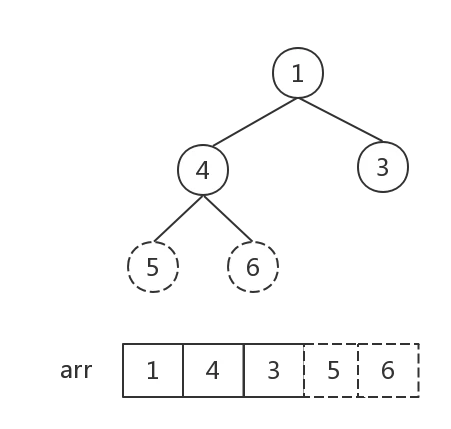
步骤3
接下来反复执行步骤2,直到堆中元素个数为1:
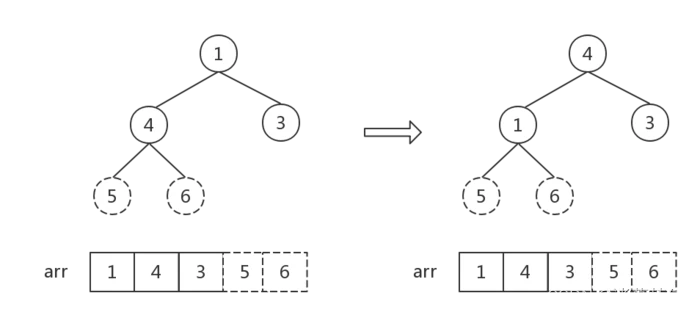
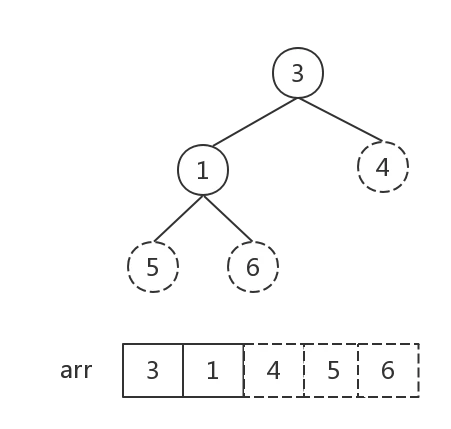
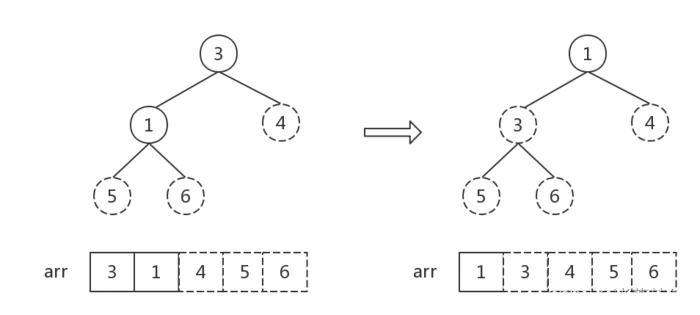
堆中元素个数为1, 排序完成。
参考文献:
