C++ 中缀表达式转后缀表达式
关于后缀表达式如何计算,这里不做过多叙述。以下提供两种方式供参考,第二个种方式粗略的写了计算方式。
方式一 —— 栈
该方式主要是通过栈的数据结构,规定运算符的优先级进行处理即可。
参考链接:https://blog.csdn.net/liudongdong19/article/details/80767156
源码(C++)
#include <iostream>
#include <map>
#include <string>
#include <stack>
using namespace std;
map<char, int> priority;
bool JudgeNumber(char s) { return s - '0' >= 0 && s - '0' <= 9 ? true : false; }
int GetPriority(char c)
{
auto iter = priority.find(c);
return iter == priority.end() ? -1 : iter->second;
}
string GetSuffix(string prefixStr)
{
string suffixStr;
stack<char> s;
s.push('#');
while (!prefixStr.empty())
{
//如果是数字或者小数那么直接加入后缀表达式
if (JudgeNumber(prefixStr[0]) || prefixStr[0] == '.')
{
suffixStr.push_back(prefixStr[0]);
prefixStr.erase(prefixStr.begin());
}
else
{
//当中缀表达式第一个字符为左括号时不进行判断
if (!suffixStr.empty())
{
//只有上一个数是数字,才添加空格;否则的话数字和数字之间不会有空格,也就无法区分是否为同一个数字
if (JudgeNumber(suffixStr.back()))
suffixStr.push_back(' ');
}
//如果是右括号的话,输出所有的操作运算符直至遇到左括号,并抛弃这一对括号
if (prefixStr[0] == ')')
{
while (s.top() != '(')
{
suffixStr.push_back(s.top());
s.pop();
suffixStr.push_back(' ');
}
prefixStr.erase(prefixStr.begin());
s.pop();
}
else if (prefixStr[0] == '(')//如果是左括号的话,直接入栈
{
s.push(prefixStr[0]);
prefixStr.erase(prefixStr.begin());
}
else if (GetPriority(prefixStr[0]) > GetPriority(s.top()))//如果中缀表达式中符号的优先级大于栈顶的符号优先级则直接入栈
{
s.push(prefixStr[0]);
prefixStr.erase(prefixStr.begin());
}
else if (GetPriority(prefixStr[0]) <= GetPriority(s.top()))//如果中缀表达式中符号的优先级小于等于栈顶符号的优先级那么直接将栈中运算符添加至后缀表达式中。如果遇到左括号,则停止出栈,否则所有数据均出栈
{
while (s.top() != '(' && s.top() != '#')
{
suffixStr.push_back(s.top());
suffixStr.push_back(' ');
s.pop();
}
s.push(prefixStr[0]);
prefixStr.erase(prefixStr.begin());
}
}
}
while (s.top() != '#')
{
suffixStr.push_back(' ');
suffixStr.push_back(s.top());
s.pop();
}
return suffixStr;
}
int main()
{
priority = { {'#',0},{'(',1}, {'+',3},{'-',3} ,{'*',5},{'/',5},{')',6} };
//string s = "2*(3*5+2)+7/1-4";
//string s = "8+4-6*2";
//string s = "2*(3+5)+7/1-4";
//string s = "12*(3+4)-6+8/2";
string s = "(2+3)*2";
cout << GetSuffix(s) << endl;
return 0;
}
方式二 —— 二叉树
思路如下(以下思路仅供参考):
??比如对于中缀表达式:2*(3*5+2)+7/1-4,我们使用一个vector<string>的动态数组存储数字(整型和非整数);使用stack<char>存储运算符号,由于优先级的关系,我们使用’#'来表示最低优先级(其它符号均可)。
??现假定动态数组vector<string> arr和stack<char> s,一开始第一轮我们将2插入至arr,‘*‘的优先级比’#‘高,直接插入s中,但是由于当前没有两个以上数字,所以我们继续处理中缀表达式,s中插入’(‘运算符,之后一直处理数字和符号(s中如果有’(‘运算符则直接无条件插入),直至遇到’)‘符号,此时,当前arr = {2,3,5,2},s = {’#’,‘*’,‘(’,‘*’,‘+’};我们对括号中的符号以及相应数字进行处理,结果如下:
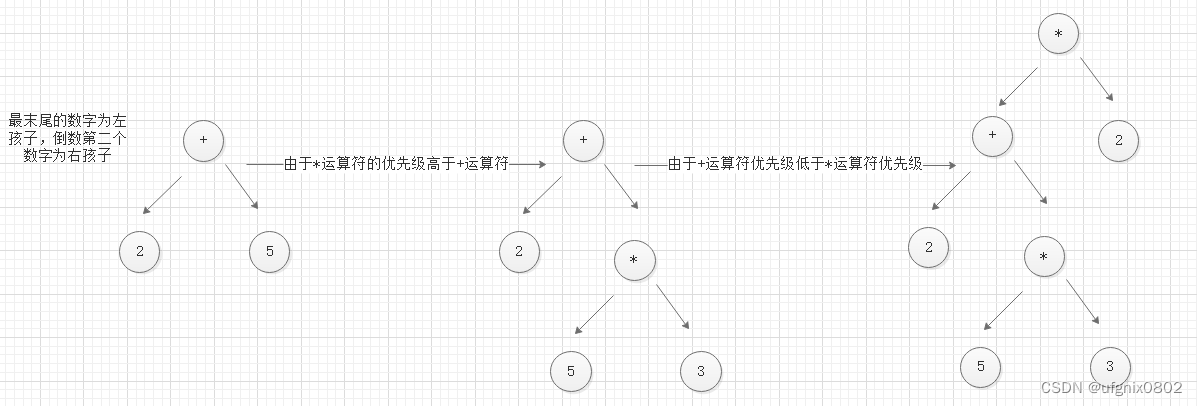
??此时中缀表达式只剩下:+7/1-4。继续处理,如下:
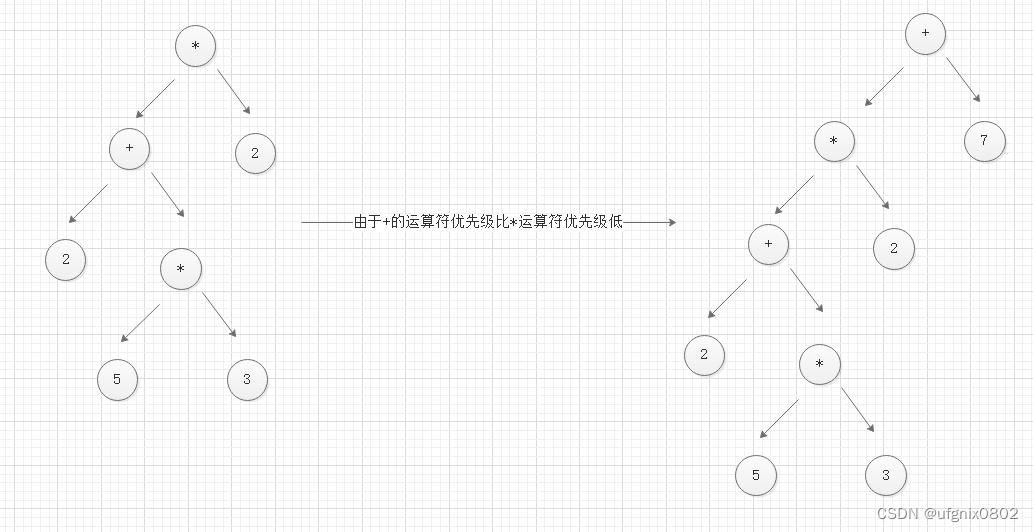
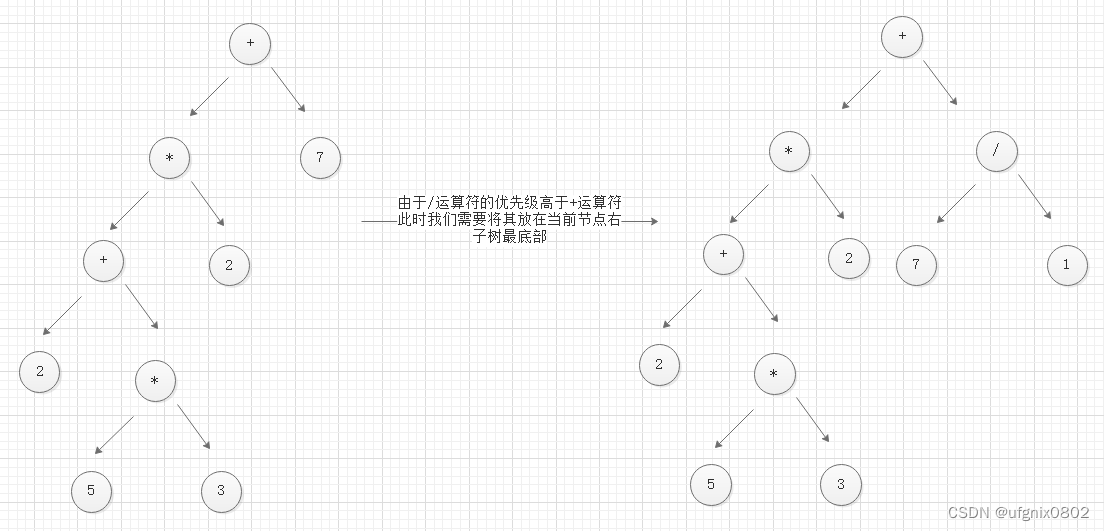
??最后,将剩余的符号和数字进行处理。
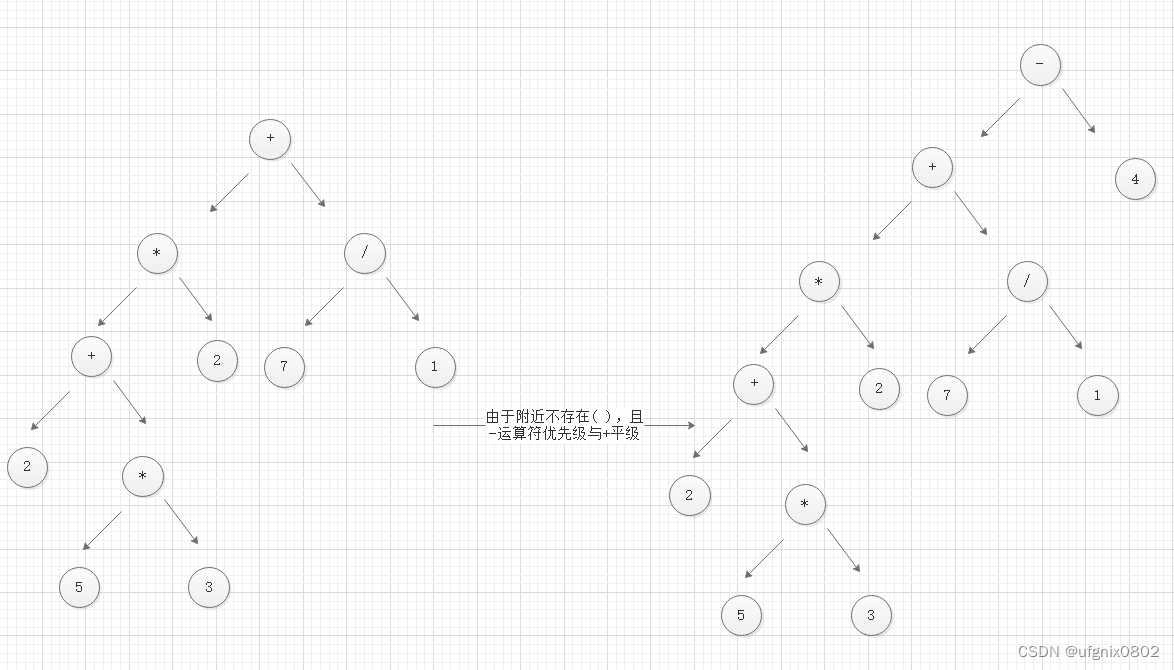
源码(C++)
#include <iostream>
#include <string>
#include <vector>
#include <stack>
#include <map>
#include <algorithm>
using namespace std;
static map<char, int> priority;
//二叉树结构
struct TreeNode
{
TreeNode* left;
TreeNode* right;
string val;
TreeNode(string val_) :left(nullptr), right(nullptr), val(val_) {};
};
//判断是否为数字
static bool JudgeNumber(char s) { return s - '0' >= 0 && s - '0' <= 9 ? true : false; }
//判断优先级
static int GetPriority(char c)
{
auto iter = priority.find(c);
return iter == priority.end() ? -1 : iter->second;
}
//判断当前栈中是否包含'('操作符
static bool IsLeftSymbol(stack<char> stacks)
{
while (!stacks.empty())
{
if (stacks.top() == '(')
return true;
stacks.pop();
}
return false;
}
//在当前节点的右子树最下方重新构建一个单元的二叉树,
//比如:
// +
// / \
// 3 5
//如果c='*',rightNum=8,则
// +
// / \
// 3 *
// / \
// 5 8
void SetRightTree(TreeNode* curNode, char c, string rightNum)
{
stack<TreeNode*> stacks;
while (curNode->right != nullptr)
{
stacks.push(curNode);
curNode = curNode->right;
}
TreeNode* node = new TreeNode(string(1, c));
node->left = stacks.top()->right;
node->right = new TreeNode(rightNum);
stacks.top()->right = node;
}
//在当前节点上方重新构建一个单元的二叉树,
//比如:
// +
// / \
// 5 6
//如果s = {#,-},arr = {6};则
// -
// / \
// + 6
// / \
//5 6
void SetTopTree(stack<char>& s, vector<string>& arr, TreeNode*& curNode)
{
if (arr.size() == 0)return;
TreeNode* node = new TreeNode(string(1, s.top()));
s.pop();
node->left = curNode;
node->right = new TreeNode(arr[arr.size() - 1]);
arr.pop_back();
curNode = node;
}
//设计一个单元的二叉树(一个父节点,两个子节点)
void SetRootNode(stack<char>& s, vector<string>& arr, TreeNode*& curNode)
{
curNode = new TreeNode(string(1, s.top()));
s.pop();
curNode->left = new TreeNode(arr[arr.size() - 1]);
arr.pop_back();
curNode->right = new TreeNode(arr[arr.size() - 1]);
arr.pop_back();
}
//根据不同的情况(运算符的优先级)构建不同的二叉树单元
void SetTree(stack<char>& s, vector<string>& arr, TreeNode*& curNode, bool flag)
{
if (curNode == nullptr)
SetRootNode(s, arr, curNode);
else if (GetPriority((curNode->val[0])) < GetPriority(s.top()) && !flag)//如果当前父节点的优先级小于栈顶运算符的优先级
{
SetRightTree(curNode, s.top(), arr[arr.size() - 1]);
s.pop();
arr.pop_back();
}
else if (GetPriority((curNode->val[0])) >= GetPriority(s.top()) || flag)//如果当前父节点的优先级大于等于栈顶运算符的优先级
SetTopTree(s, arr, curNode);
}
//构建二叉树,用于计算中缀表达式
TreeNode* GetPrefixTree(string str)
{
TreeNode* beginNode = nullptr;
vector<string> arr;
stack<char> s;
s.push('#');
bool flag = false;
while (!str.empty())
{
//如果当前不存在'('符号且beginNode未初始化,同时arr中有两个数字。(保证第一次直接构架一个基础二叉树单元)
if (!IsLeftSymbol(s) && beginNode == nullptr && arr.size() == 2)
SetRootNode(s, arr, beginNode);
//如果是数字或者小数那么直接记录下来
if (JudgeNumber(str[0]))
{
int count = 0;
while (count < str.size())
{
if (str[count] == '.' || JudgeNumber(str[count]))count++;
else break;
}
arr.push_back(string(str.begin(), str.begin() + count).c_str());
str.erase(str.begin(), str.begin() + count);
}
else//此时为运算符(+,-,*,/)或者'('和')'
{
if (str[0] == ')')//如果为')'符号,则处理当前数据
{
str.erase(str.begin());//去除')'
while (s.top() != '#')
{
if (s.top() == '(')
{
s.pop();
flag = true;
continue;
}
SetTree(s, arr, beginNode, flag);//构建二叉树
}
if (GetPriority(str[0]) >= GetPriority(beginNode->val[0]))//这个是用于判断比如(3+5)*2和2*(3+5),即如果括号在右侧,flag为true,此时不需要按照优先级判断。
flag = true;
else
flag = false;
}
else if (str[0] == '(')//此时无条件入栈
{
s.push(str[0]);
str.erase(str.begin());
}
else if (IsLeftSymbol(s))//如果栈中有'('符号,则运算符号直接入栈
{
s.push(str[0]);
str.erase(str.begin());
}
else if (GetPriority(str[0]) >= GetPriority(s.top()))//如果当前表达式中的符号优先级大于等于栈顶符号优先级
{
//如果此时二叉树中已经有节点,则接着处理
if (beginNode != nullptr && s.top() != '#')
SetTopTree(s, arr, beginNode);
s.push(str[0]);
str.erase(str.begin());
}
else if (GetPriority(str[0]) < GetPriority(s.top()))//如果当前表达式中的符号优先级小于栈顶符号优先级
{
SetTree(s, arr, beginNode, flag);
s.push(str[0]);
str.erase(str.begin());
}
}
}
if (beginNode != nullptr)//将最后剩余的元素进行处理
SetTree(s, arr, beginNode, flag);
return beginNode;
}
//计算二叉树
double GetValue(TreeNode* node)
{
if (!JudgeNumber(node->val[0]))
{
if (node->val == "+")
return GetValue(node->left) + GetValue(node->right);
else if (node->val == "-")
return GetValue(node->left) - GetValue(node->right);
else if (node->val == "*")
return GetValue(node->left) * GetValue(node->right);
else
return GetValue(node->left) / GetValue(node->right);
}
else
return atof(node->val.c_str());
}
int main()
{
priority = { {'#',0},{'(',1}, {'+',3},{'-',3} ,{'*',5},{'/',5},{')',6} };
//string s = "2*(3+5)+7/1-4";
//string s = "8+4-6*2";
//string s = "2.4234*(3+5)+7/1-4";
string s = "2*(3*5+2)+7/1-4";
//string s = "12*(3+4)-6+8/2";
//string s = "(2+3)*2";
TreeNode* node = GetPrefixTree(s);
double res = GetValue(node);
cout << GetValue(node) << endl;
return 0;
}
