圆形,在初中和高中时我们经常学到,也做过不少关于圆形的数学题,
?今天我就要用数学知识来打印一个圆,编程不开数学,我们要学以致用。
思路 :打印圆形的思路很简单,首先定义一个正方形,这个正方形比较特殊,它是以坐标来打印的 ,利用x 和 y 如图所示
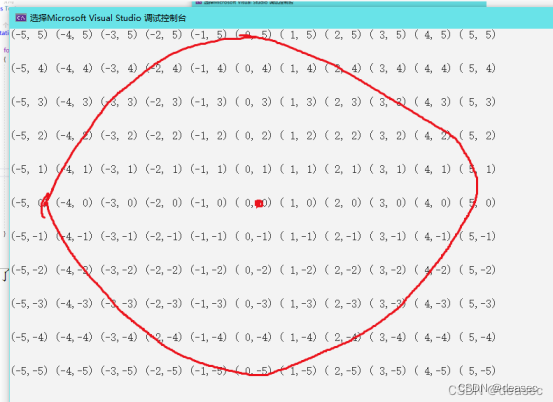
?
有了坐标可以想到使用坐标 来画圆形,
然后定义一个方法InputRadius,输入一个数会输出圆形,这个数是圆形的半径,这个正方形的边长是 两倍的半径+1
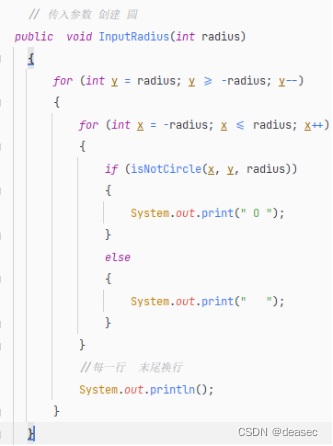
?
这里的x和y其实就是 初中学的直角坐标系的对应的 x和y,然后根据x和y判断一个正方形中的圆,就像数学题中正方形中求圆形的阴影面积一样,如果可以做出一个方法函数判断x,y是否在圆内,很简单,利用到初中学的勾股定理就能搞定,将上面的x和y和半径传入一个isNotCircle方法中作为实参,这个方法代码如下:
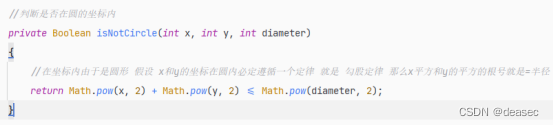
?
我来讲解一下这一段代码的意思, 我用传入参数x的平方+y的平方的值比较传入半径的平方的值, 如果小于或等于半径的平方的话,那么就是在圆的范围内。最后看效果图我输入一个半径为20的圆,半径越大越像圆,半径不能小于10:

?
最后是完全的代码
public class Circle {
// 传入参数 创建 圆
public void InputRadius(int radius)
{
for (int y = radius; y >= -radius; y--)
{
for (int x = -radius; x <= radius; x++)
{
if (isNotCircle(x, y, radius))
{
System.out.print(" O ");
}
else
{
System.out.print(" ");
}
}
//每一行 末尾换行
System.out.println();
}
}
//判断是否在圆的坐标内
private Boolean isNotCircle(int x, int y, int diameter)
{
//在坐标内由于是圆形 假设 x和y的坐标在圆内必定遵循一个定律 就是 勾股定律 那么x平方和y的平方的根号就是=半径
return Math.pow(x, 2) + Math.pow(y, 2) <= Math.pow(diameter, 2);
}
public static void main(String[] args) {
Circle circle=new Circle();
circle.InputRadius(15);
}
}
