
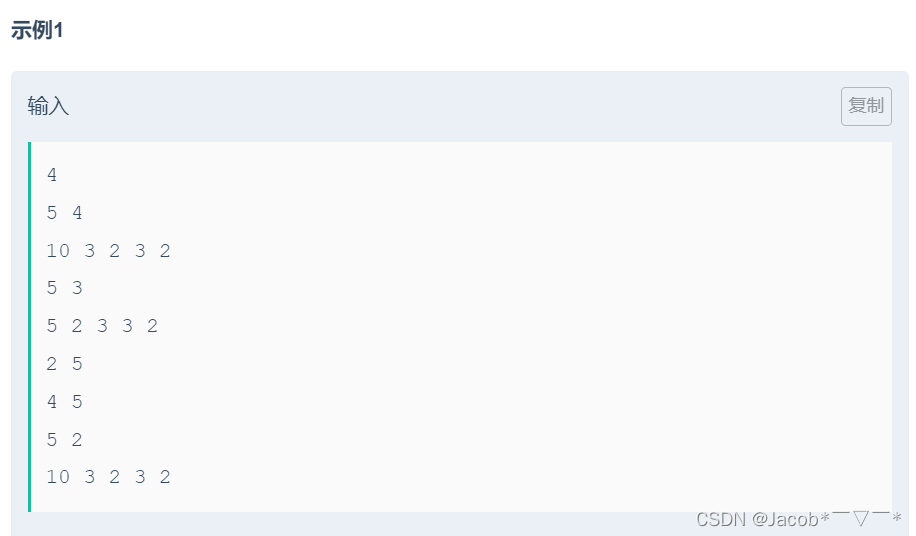
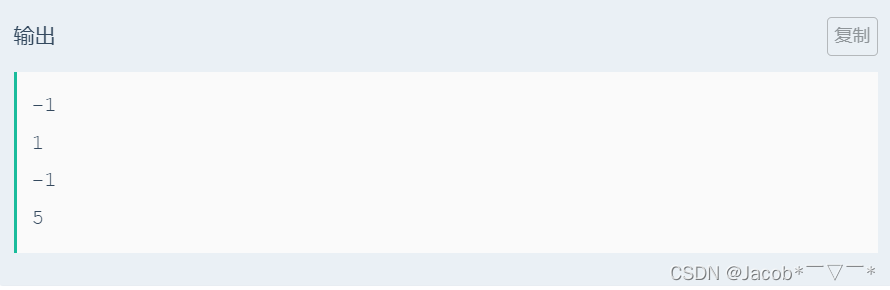
题意:
给定一个 长为 n 的数组 a 和 一个整数 m,你需要将其 切成连续的若干段,使得 每一段的中位数 都 大于等于 m,求 最多可以划分成多少段。
思路:
这是一道十分有趣的题目,预期的简单解法 O(n) ,复杂解法 O(nlogn) 。
一、简单解法:
记 数列中 ≥ m 的数字 有 cnt1 个,< m 的数字 有 cnt2 个,则 答案为 cnt1 - cnt2,该值 ≤ 0 时输出 -1
证明一(严谨):
记 f(l, r) 为 原数组中 a[l],...,a[r] 一段中的元素 对应的 cnt1 - cnt2 的值
f() 的性质:
-
f(l, r) > 0表示该段单独拿出来满足中位数≥ m -
f(l, r) = f(l, mid) + f(mid + 1, r)
原问题 f(1, n) ≤ 0 时 输出 -1 是显然的。
欲证明:
f(1, n) > 0 时,f(1, n) 即为原问题答案。
考虑 初始 所有数组成了一个大区间,我们在通过 切大区间 为 若干段 来得到 最终答案。
若可以 找到一个位置 mid,使 f(1, mid) > 0 && f(mid + 1, n) > 0,则 沿 mid 将数组切开 得到的 两部分中位数 依然 满足条件,此时 区间数 += 1。
所以我们要探究 什么时候数组可以切?
定理:
当且仅当 f(l, r) > 1 时 存在 一种切法 mid 使 f(l, mid) > 0 && f(mid + 1, r) > 0
证明:
若 有一个位置 mid 使得 f(l, mid) = 1,则 该位置 是 满足条件的切割位置,因为 此时 f(l, mid) = 1 > 0, f(mid + 1, r) = f(l, r) - f (l, mid) > 1 - 1 = 0。
又因为 f(l, l - 1) = 0(表示 空区间)且 f(l, r) > 1 且 f(l, x) -> f(l, x + 1) 时 值只会变化 1,因此过程中 一定存在某一时刻 mid 使得 f(l, mid) = 1。
由上,只要 f(l, r) > 1 就可以切,而我们又希望 切得尽可能多,因此 最终状态 一定是 所有切割得到的段都有 f(l, r) = 1 (否则 还可以再切)。
因此,

又因为 初始时 有
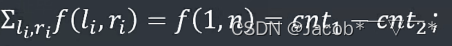
所以 最终切成的段数 = cnt1 - cnt2,证毕。
证明二(不严谨):
先假设 数组里只有 ≥ m 的数字们(想象有一个 只含 ≥ m 的数 的 长为 cnt2 的数组),他们都自己作为一个区间,则 一共有 cnt1 个区间,且这些区间都是 满足中位数 ≥ m 的要求 的。
然后考虑 插一个 < m 的数字进去,这个数字 需要和 两个 > m 的数组 组成一个区间 才可以 满足中位数要求,因此 原来两个区间变成了一个区间,区间数减一,然后 删掉这个数 和 某个 > m的数,数组长变为 cnt2 - 1。
(你可能会说这 cnt2 - 1 里有一个数其实是在刚才新组成的区间里,这没问题吗,但 这种新组成的区间并不影响上述操作,所以 可以看作一个 > m 的数字)
以此类推,可以看出 每个 < m 数字的作用就是说区间数减一。
二、复杂解法:(借鉴一位大佬博主)
使用 线段树 + 前缀和 + DP,将 O(n ^ 2) 的 DP 优化到 O(nlogn)。
划分满足 无后效性,想到 dp,则设:dp[i] 表示 考虑前 i 个元素,最多划分 的 段数。
看到 中位数,想到把元素变化。若 ai ≥ m ,即为 1,否则记为 -1
这样,序列的 中位数 ≥ m 转化为 序列的和 ≥ 1
dp 的转移,如下:

元素和,想到 前缀和。我们用 pre 数组记录前缀和(代码中用 s 数组表示),于是后面就变成了:
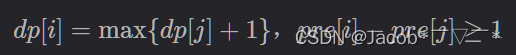
由于 pre[i] 是固定的,我们 移动元素位置,得到:
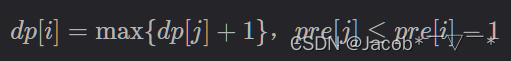
于是,右边就变成了 求区间最大值,线段树 搞定。
最后 答案当然就是 dp[n]
注意到,pre 数组是可以为负数的,所以我们 每个位置的元素增加一个增量 M = 1e5 + 5 即可。
还注意到,有些位置的分隔是不可行的,因为求的是 区间最大值,用 -1 做初始化。
代码:(做法一)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
ll num[N];
int main()
{
int t; scanf("%d", &t);
while(t--)
{
int n, m; scanf("%d%d", &n, &m);
int a = 0, b = 0;
for(int i=0; i<n; ++i)
{
scanf("%lld", &num[i]);
if(num[i]>=m) ++a;
else ++b;
}
int ans = a - b;
if(ans > 0) printf("%d\n", ans);
else puts("-1");
}
return 0;
}
代码:(更新做法二 线段树优化dp + 前缀和)
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
const int M = N>>1;
struct node
{
int l, r;
int v;
} t[N<<2];
int s[N];
void pushup(int u)
{
t[u].v = max(t[u<<1].v, t[u<<1|1].v);
}
void build(int u, int l, int r)
{
t[u] = {l, r};
if(l==r) {t[u].v = -1; return ;}
int mid = l + r >> 1;
build(u<<1, l, mid), build(u<<1|1, mid+1, r);
pushup(u);
}
void modify(int u, int x, int v)
{
if(t[u].l==x&&t[u].r==x) {t[u].v = v; return ;}
int mid = t[u].l + t[u].r >> 1;
if(x<=mid) modify(u<<1, x, v);
if(x>mid) modify(u<<1|1, x, v);
pushup(u);
}
int ask(int u, int l, int r)
{
if(l<=t[u].l&&r>=t[u].r) return t[u].v;
int res = -1;
int mid = t[u].l + t[u].r >> 1;
if(l<=mid) res = max(res, ask(u<<1, l, r));
if(r>mid) res = max(res, ask(u<<1|1, l, r));
return res;
}
int main()
{
int t; scanf("%d", &t);
while(t--)
{
int n,m; scanf("%d%d",&n,&m);
for(int i=1; i<=n; ++i)
{
int t; scanf("%d",&t);
s[i] = s[i-1] + (t>=m ? 1 : -1);
}
build(1, 1, N);
modify(1, 0 + M, 0);
int ans = -1;
for(int i=1; i<=n; ++i)
{
int dpj = ask(1, 1, s[i] - 1 + M);
if(dpj!=-1)
{
int dpi = dpj + 1;
if(i==n) ans = dpi;
modify(1, s[i] + M, dpi);
}
}
printf("%d\n", ans);
}
return 0;
}
