-
第一题
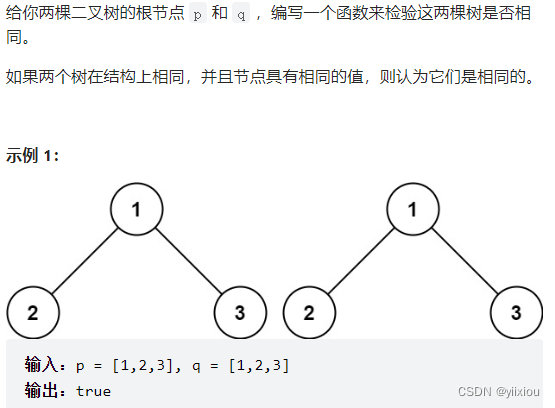
方法一:深度优先搜索
(1)两个二叉树都为空,则相同。
(2)两个二叉树只有一个为空,则不相同。
(3)两个二叉树都不为空,可以判断根节点的值,若根节点的值相同再判断二叉树的左子树是否相同、右子树是否相同。/** * Definition for a binary tree node. * struct TreeNode { * int val; * struct TreeNode *left; * struct TreeNode *right; * }; */ bool isSameTree(struct TreeNode* p, struct TreeNode* q){ //两个二叉树都为空,一定相同 if(p==NULL && q==NULL) { return true; } else if ((p==NULL && q!=NULL) || (p!=NULL && q==NULL)) //两个二叉树只有一个为空,说明一定不相同 { return false; } else if(p->val!=q->val) //根节点值不相同,说明一定不相同 { return false; } else{ return isSameTree(p->left,q->left) && isSameTree(p->right,q->right); //递归遍历左右子树 } }方法二:使用迭代方法实现
-
第二题(二叉树的中序遍历)
中序遍历:根节点在中间访问,正常顺序是左子树、根节点、右子树。
方法一:递归。
void inorder(struct TreeNode* root,int* res,int* resSize) { if(!root) //空节点推出 { return; } inorder(root->left,res,resSize); res[(*resSize)++]=root->val; inorder(root->right,res,resSize); } int* inorderTraversal(struct TreeNode* root, int* returnSize){ int* res=malloc(sizeof(int)*501); *returnSize=0; inorder(root,res,returnSize); return res; }方法二:迭代:
int* inorderTraversal(struct TreeNode* root, int* returnSize) { *returnSize = 0; int* res = malloc(sizeof(int) * 501); struct TreeNode** stk = malloc(sizeof(struct TreeNode*) * 501); int top = 0; while (root != NULL || top > 0) { while (root != NULL) { stk[top++] = root; root = root->left; } root = stk[--top]; res[(*returnSize)++] = root->val; root = root->right; } return res; } -
第三题(二叉树的后序遍历)
后序遍历:根节点在最后访问,正常顺序是左子树、右子树、根节点,但是需要判断右子树是否存在,如果不存在,左节点后的节点是根节点。
方法一:递归
void inorder(struct TreeNode* root,int* res,int* resSize) { if(!root) //空节点推出 { return; } inorder(root->left,res,resSize); inorder(root->right,res,resSize); res[(*resSize)++]=root->val; } int* postorderTraversal(struct TreeNode* root, int* returnSize){ //后序遍历,左子树、右子树、根节点 int* res=malloc(sizeof(int)*2001); *returnSize=0; inorder(root,res,returnSize); return res; }方法二:迭代
/** * Definition for a binary tree node. * struct TreeNode { * int val; * struct TreeNode *left; * struct TreeNode *right; * }; */ /** * Note: The returned array must be malloced, assume caller calls free(). */ int* postorderTraversal(struct TreeNode* root, int* returnSize){ //根节点最后,左子树,右子树,根节点 int* res = malloc(sizeof(int)*2001); *returnSize=0; if(root==NULL){ return res; } struct TreeNode** stk = malloc(sizeof(struct TreeNode*) *2001); int stk_top=0; struct TreeNode *prev = NULL; while(stk_top>0 || root !=NULL) { while(root != NULL) { stk[stk_top++] = root; root = root->left; } root = stk[--stk_top]; if(root -> right==NULL || root->right ==prev) //无右子树的情况,更新根节点 { res[(*returnSize)++] = root->val; prev=root; root=NULL; } else //正常迭代右子树 { stk[stk_top++] =root; root = root->right; } } return res; } -
第四题(二叉树的前序遍历)
前序遍历:根节点在首尾,顺序是根节点、左子树、右子树。
方法一:递归。
void inorder(struct TreeNode* root,int* res,int* resSize) { if(!root) //空节点推出 { return; } res[(*resSize)++]=root->val; inorder(root->left,res,resSize); inorder(root->right,res,resSize); } int* preorderTraversal(struct TreeNode* root, int* returnSize) { //前序遍历,根节点在首位,根节点、左子树、右子树 int* res = malloc(sizeof(int) * 2000); *returnSize = 0; inorder(root,res,returnSize); return res; }方法二:迭代。
int* preorderTraversal(struct TreeNode* root, int* returnSize) { //前序遍历,根节点在首位,根节点、左子树、右子树 int* res = malloc(sizeof(int) * 2000); *returnSize = 0; if (root == NULL) { //如果根节点为空,直接返回空 return res; } struct TreeNode* stk[2000]; struct TreeNode* node = root; int stk_top = 0; while (stk_top > 0 || node != NULL) { while (node != NULL) { res[(*returnSize)++] = node->val; stk[stk_top++] = node; node = node->left; } node = stk[--stk_top]; node = node->right; } return res; }
