项目地址???????How Does a Database Work? | Let’s Build a Simple Database (cstack.github.io)。
如果你还不知道什么是b+树,请阅读网站上相关内容。如果还不懂,请在网上查相关资料。
如果不会b+树,之后的内容就等于天书。
上述内容至少得看一个小时吧,从原理到设计实现,都可以看挺久的。
如果你不想找或者还没看懂,那么就往下翻。
我也是看博客及百度百科的,他们说的太权威了,我这里就尽量以最容易理解的方式说明。
能不能往下走就看各位了,加油!
1.你给我翻译翻译,树是什么?
树嘛,就是树。这还用翻译?(bushi)一种数据类型结构。(呵呵,听君一席话,如听一席话。)你看数组,我们拿指针遍历a[0]是第一个,a[1]是第二个,它就是一维的结构。而树是二维的结构,如图。

?你看,它从根部分叉了,分成了多个枝丫,每个枝丫它又分叉,一直到叶子为止。
我们抽象一点,为了记录一颗树,我们用节点来表示位置,用指针指向下一个节点。叶子我就不画了,太麻烦了。我们把图中这棵树最下面的节点叫做根节点,把枝丫叫做内部节点,把叶子称为叶节点。节点的上一层叫做父节点,下一层叫做子节点。(是节点还是结点,我傻傻的分不清,反正就这么叫吧。)
而把树倒过来看,就是我们研究的内容了。(为什么要倒过来看呢?我也不知道。可能是方便吧)。
2.你给我翻译翻译,b+树是什么?
你看上图的树,它垂直向上的节点多一些,而左边的节点少一些。而b+树,一个名字中有balance的树,它的节点应该一样多。
别忘了我们是写数据库的,数据放哪里呢?我们放叶子节点里,因为叶子多。那么怎么找数据呢?为了方便的找数据,我们把数据从小到大排列(比如说我们的id)并依次放入叶子中(从左到右排),叶子一个一个的连着(就类似与铁索连营,这里省略)。有人问,树不是二维的吗?怎么叶节点成一维的了?这是因为b+树节点一样多,那么对于每个叶节点,他们应该都在同一层。枝丫承受的叶子重量有限,但作为一颗健康的树,它靠近叶子的枝丫至少也有一些树叶。假设这里有两片树叶,一个叶子数据存的1,5,另一个存的12。作为连接两个树的枝丫,我们假设就存左边节点中最大的那个数(也可以是右边节点最小的),这里是5。那么如果找1或5,就去左边的叶子,如果找12,就去右边的叶子。找到叶子后,就找到了该id存储的数据,非常方便。
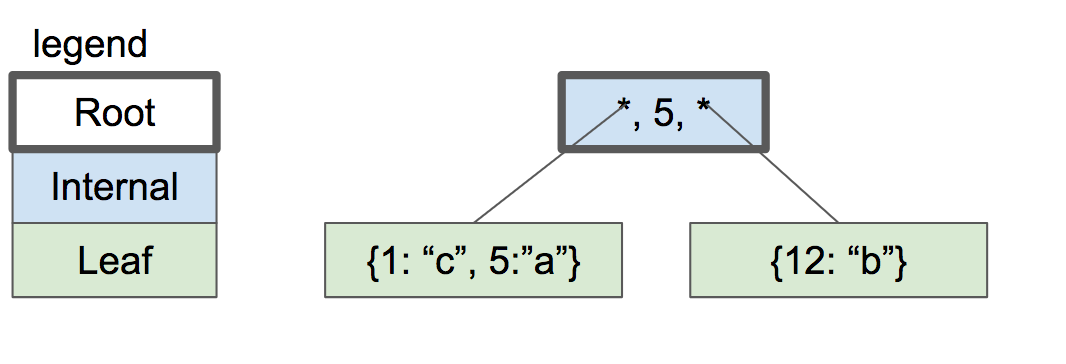
当然,不是所有b+树,它最多只有两个子节点,它可能有多个节点。它的父节点就存除了最右边的子节点的最大值。(如果是存的最小值,则是除左边的子节点的最小值。)
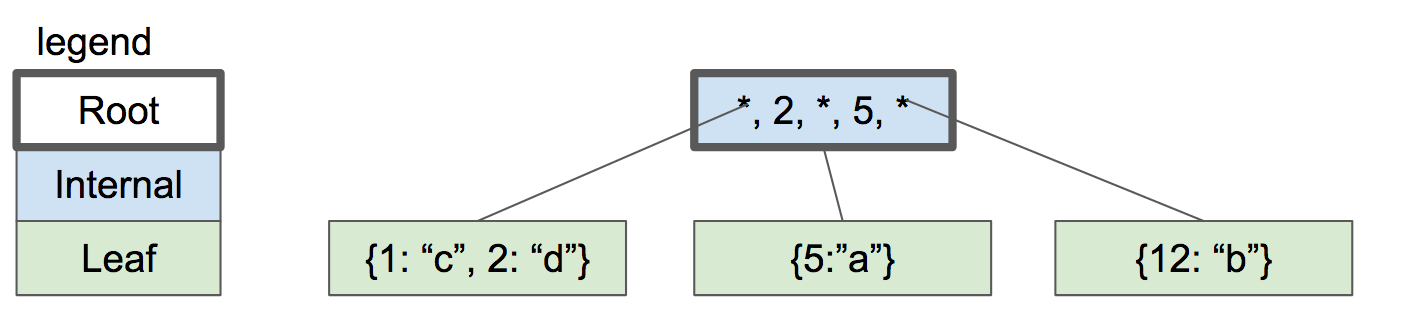
当然不是所有的树都只有两层,大的b+树应该有很多很多层。也就是说,枝丫有可能不连接树叶,它可能连接枝丫。同一层的枝丫也是从小到大排,它们的上一层依旧是左边节点的叶节点的最大值。(如果是存的最小值,则是右边节点的叶节点的最小值。)
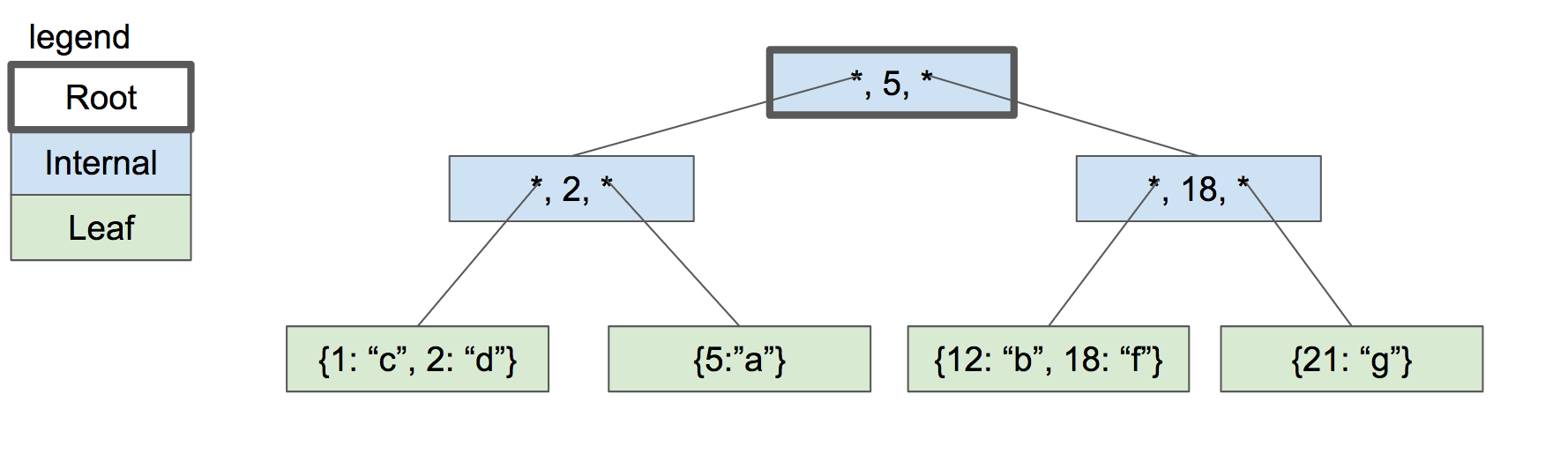
那么我们再说细一点,如何查找?如何插入?如何删除?
这里我们说说“阶”。什么是阶?我理解为限制节点个数的。不然我就一片叶子,里面装所有数据,那肯定是不合理的。同理,明明可以多个数据被装在一个叶子的,我一个叶子装一个数据,那也是不合理的。我们说一个m阶的b+树,叶子数据要大于等于m/2且小于等于m-1,内部节点项的个数要大于等于m/2且小于等于m-1。
好了,先说查找吧,查找是最简单的。对于3阶b+树,我们拿上面那张图举例从根节点开始,小于或等于在左边,大的在右边。比如我们查找12,12比5大,故到右边的子节点。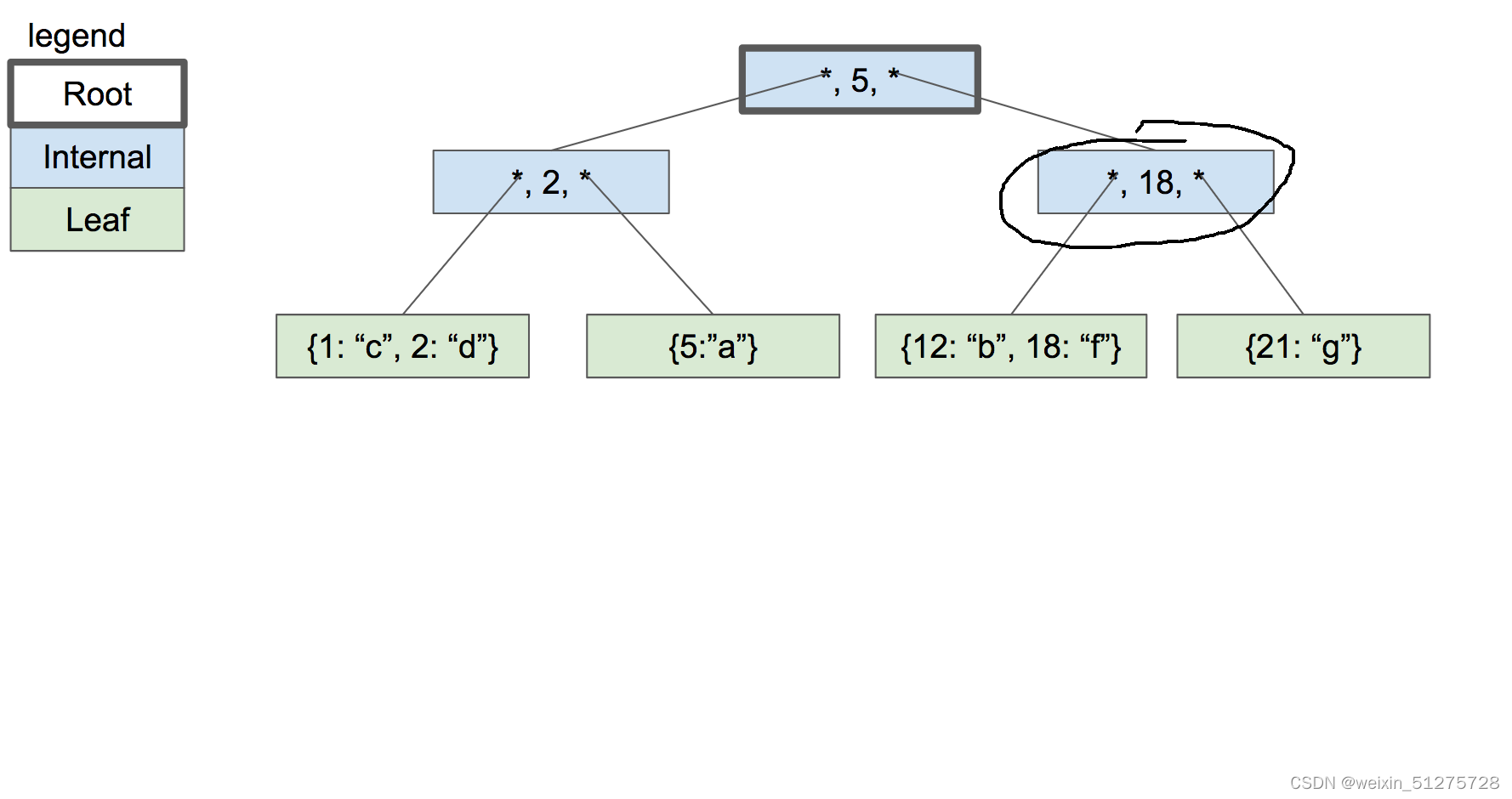
12比18小,故去左边的子节点。然后就找到12了。?
接下来是一颗4阶的b+树,找的别人博客的。
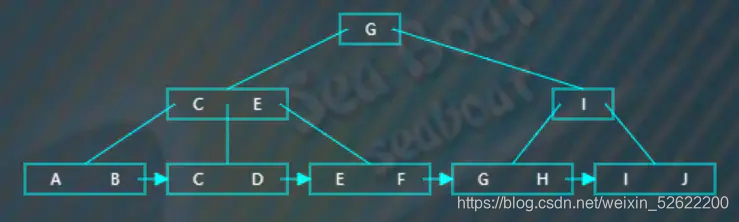
?它父节点存放的就是子节点右最小值。那么小于在左边的子节点,大于等于在右边的子节点。
比如我们找D,D小于G,故去左边的子节点。这时候,C<D<E,怎么办呢?当然是去中间的子节点了。查找就是这样,没什么难度。
怎么插入呢?m阶B+树插入要记住这几个步骤:
1.B+树插入都是在叶子结点进行的,就是插入前,需要先找到要插入的叶子结点。
2.如果被插入关键字的叶子节点,当前含有的关键字数量是小于阶数m,则直接插入。
3.如果插入关键字后,叶子节点当前含有的关键字数目等于阶数m,则分成两个节点。
4.分裂后,需要将中间的关键字上移到父结点。如果这时候父结点中包含的关键字个数小于m,则插入操作完成。
5.分裂后,需要将中间的关键字上移到父结点。如果父结点中包含的关键字个数等于m,则继续分裂父结点。直到小于m为止。
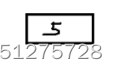
那么我们再来插入操作。假设是个3阶b+树。我们依次插入? 5,1,2,3,6,9,11,4,8,。首先插入5
?插入1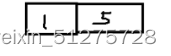
?插入2,超出一个节点了,分成两个节点,根节点存放左边节点中最大的。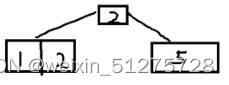
?插入3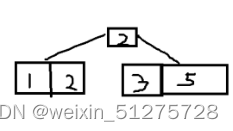
插入6 把3,5,6分成两个节点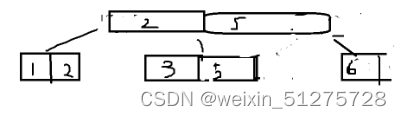
?插入9?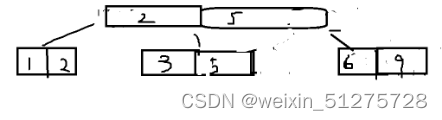
插入11? ?6,9,11分成两个节点,9保存在上一层节点,根节点分层
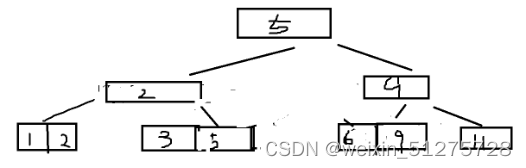
插入4 3,4,5节点分成两个节点 4保存在上一个节点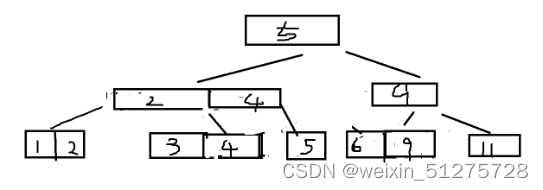 ?
?
插入8 6,8,9分成两个节点,8保存在上一个节点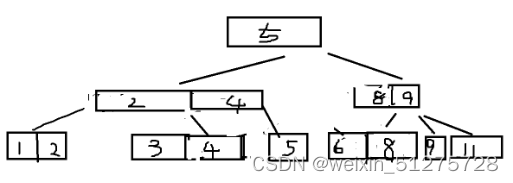 ?
?
最后,如何删除呢?
1.如果该叶子存放的内容大于m/2,就直接删除,如果父节点中还存着这个值,那么也应该相应调整。
2.如果该叶子存放的内容等于m/2,删除后这叶节点就不满足最少存放内容个数,这时候就找周围的(其父节点下面的所有节点)有多于这标准的叶节点借,当然如果父节点中还存着这个值,父节点也有相应调整。
3.如果周围没多的,那就合并两个叶节点。

比如这个图,我想删除E节点。首先它是一颗4阶b+树,叶节点至少要两个内容,对于周围节点都没有多的,那么c,d,f就合在一起,其父节点的E去掉。
以上就是所有内容了,喜欢的可以点个赞哦!
