今天我们浅谈一下树上操作的边分治,首先我们要了解一下为什么要使用边分治,当我们处理问题的规模很大时,用暴力的方法O(n^2)会导致时间超时,而使用边分治,点分治每次会将树分为将近n/2的子树,所以点分治,边分治会将时间复杂降为O(nlogn)。
边分治是指在给定的一个树中,找到一条边(中心边),将这条边删去,使得删去这条边后分成的两个子树的大小尽可能相等。边分治和点分治所解决的问题基本上是相同的,但是基于边的分治只需要考虑两棵子树,所以设计算法更为简单。找中心边的方法和找重心的方法一样,找使最大子树尽可能小的那一条边。
假设中心边为x-y,则树中任意两个点的路径可以分为两种:经过x-y,不经过x-y。
不经过x-y的路径在以x,y为根的两个子树中,可以递归求解。
需要注意的一点是,边分治对菊花图的处理,如图:

在处理这种图的时候发现,所有路径都经过中心边,算法的时间复杂会退化为O(n^2),此时需要将树转化一下,转化树有两种方法:
第一种方法是从1开始枚举每个点,对于一个点x,如果他有<=2个子节点,那么直接向子节点连边即可;否则新建两个点,将x连向这两个点,并将x的子节点按奇偶分类暂时归为这两个新建点的子节点。为了不影响原树深度等信息,我们将连向新建点的边权设为0。这样新建树因为每条原树边会被存logn次,所以空间复杂度是O(nlogn)。
void rebuild()
{
tot=1;
for(int i=1;i<=n;i++)
{
head[i]=0;
}
for(int i=1;i<=n;i++)
{
int len=q[i].size();
if(len<=2)
{
for(int j=0;j<len;j++)
{
add(i,q[i][j],(q[i][j]<=m));
add(q[i][j],i,(q[i][j]<=m));
}
}
else
{
int ls=++n;
int rs=++n;
v[ls]=v[rs]=v[i];
add(i,ls,0);
add(ls,i,0);
add(i,rs,0);
add(rs,i,0);
for(int j=0;j<len;j++)
{
if(j&1)
{
q[ls].push_back(q[i][j]);
}
else
{
q[rs].push_back(q[i][j]);
}
}
}
}
}第二种方法是dfs整棵树,对于原树每个点x,记录一个last(初始为x),每次将lastlast连向一个子节点,并新建一个点y将lastlast连向y,然后将last改为y。同样将连向新建点的边权设为0。因为每个原树边只被保存一次,所以空间复杂度是O(n)。需要注意的是这里和线段树一样要开四倍空间。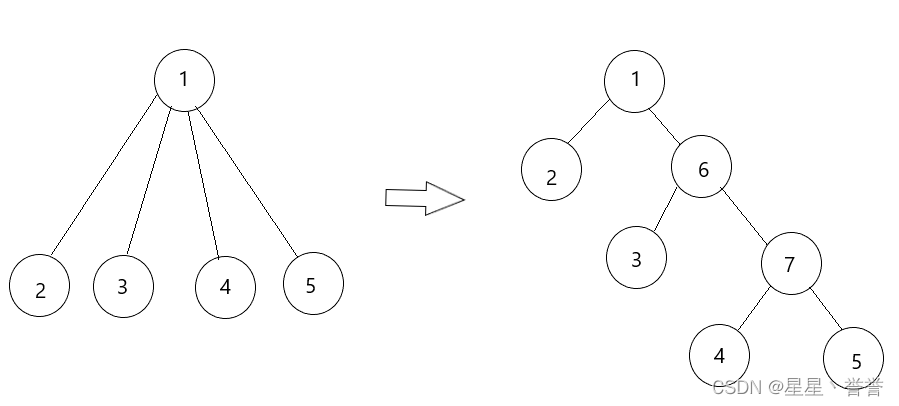
inline void rebuild(int x,int fa)
{
int tmp=0;
int last=0;
int len=v[x].size();
for(int i=0;i<len;i++)
{
int to=v[x][i].first;
int val=v[x][i].second;
if(to==fa)
{
continue;
}
tmp++;
if(tmp==1)
{
add(x,to,val);
add(to,x,val);
last=x;
}
else if(tmp==len-(x!=1))
{
add(last,to,val);
add(to,last,val);
}
else
{
m++;
add(last,m,0);
add(m,last,0);
last=m;
add(m,to,val);
add(to,m,val);
}
}
for(int i=0;i<len;i++)
{
if(v[x][i].first==fa)
{
continue;
}
rebuild(v[x][i].first,x);
}
}将图重建完毕之后就是找中心边
求中心边的方法与点分治中求中心的方法类似,只需进行一次深度优先遍历,使删除该边后的最大子树最小,代码如下:
void dfs_midedge(int u, int code)//找中心边
{
if(max(sz[u],sz[T[root].rt]-sz[u])<Max)
{
Max=max(sz[u],sz[T[root].rt]-sz[u]);//sz[T[root].rt]为该子树结点总数
midedge=code;
}
for(int i=Head[u];~i;i=E[i].nxt)
{
int v=E[i].v;
if(i!=(code^1))
dfs_midedge(v,i);
}
}接下来就是中心边分解,方法是:
(1)找出中心边midedge,得到中心边的两个端点p1,p2,然后删除p1的邻接边midedge,删除p2的邻接边midedge;
(2)分别从p1、p2出发递归求解
(3)更新树根rt的ans;
void DFS(int id, int u)
{
root=id; Max=N; midedge=-1;
T[id].rt=u;
dfs_size(u,0,0);//求解每个子树大小
dfs_midedge(u,-1);//找中心边
if(~midedge)
{
//中心边的左右2点
int p1=E[midedge].v;//p1:v midedge: u->v
int p2=E[midedge^1].v;//p2:u
cout<<"中心边:"<<endl;
cout<<p2<<"——"<<p1<<endl;
//中心边长度
T[id].midlen=E[midedge].w;
//左右子树
T[id].ls=++cnt;
T[id].rs=++cnt;
//删除中心边
Delete(p1,midedge^1);//删除p1结点的i号边
Delete(p2,midedge);
DFS(T[id].ls,p1);
DFS(T[id].rs,p2);
}
PushUP(id);//更新rt的ans
}关于边分治的例题
(2)树上查询Ⅱ(SPOJ QTREE5)
(3)树上两点之间的路径数(POJ1741)
