二叉树中和为某一值的路径(三)
描述
??给定一个二叉树root和一个整数值 sum ,求该树有多少路径的的节点值之和等于 sum 。
- 该题路径定义不需要从根节点开始,也不需要在叶子节点结束,但是一定是从父亲节点往下到孩子节点
- 总节点数目为n
- 保证最后返回的路径个数在整形范围内(即路径个数小于231-1)
数据范围:
0 <= n <= 1000
-109<= 节点值 <= 109
??假如二叉树root为{1,2,3,4,5,4,3,#,#,-1},sum=6,那么总共如下所示,有3条路径符合要求
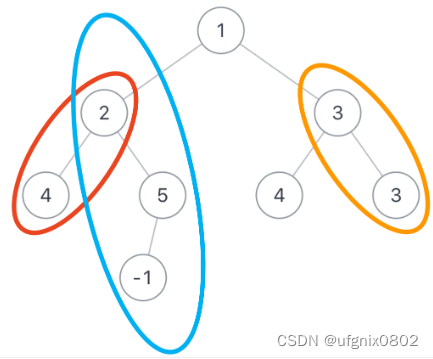
示例1
输入:
{1,2,3,4,5,4,3,#,#,-1},6
返回值:
3
说明:
如图所示,有3条路径符合
示例2
输入:
{0,1},1
返回值:
2
示例3
输入:
{1,#,2,#,3},3
返回值:
2
思路/解法
方式一
将每一层的数据存入一个一维数组中,当进入下一层的时候,上一层的数据要累加到当前下一层中,以此反复重复进行判断。
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @param sum int整型
* @return int整型
*/
void GetDepth(TreeNode* node,vector<int> arr,int& res,int sum)
{
if(node == nullptr)
return;
vector<int> newArr;
newArr.push_back(node->val);
for(int i=0;i<arr.size();i++)
newArr.push_back(arr[i]+node->val);
for(int j = 0;j<newArr.size();j++)
if(newArr[j] == sum)res++;
GetDepth(node->left, newArr, res, sum);
GetDepth(node->right, newArr, res, sum);
}
int FindPath(TreeNode* root, int sum) {
int res = 0;
vector<int> arr;
GetDepth(root, arr, res, sum);
return res;
}
};
方式二
使用一种特殊的方式进行遍历二叉树,思想为:一开始找到最左边的子树,判断当前是否有满足条件的数,没有则回退一次(到当前子树的父节点位置),往右子树继续深度查找,找到最底部判断是否有满足条件的数。之后回退,由于左右子树都已经查找过,此时应该强行回退到上一个父节点。循环反复。
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @param sum int整型
* @return int整型
*/
int FindPath(TreeNode* root, int sum) {
if (root == nullptr)return 0;
stack<TreeNode*> stacks;
vector<int> arr;
int res = 0;
while (root || !stacks.empty()) {
while (root) {
for (int i = 0; i < arr.size(); i++)
arr[i] = arr[i] + root->val;
arr.push_back(root->val);
for (int i = 0; i < arr.size(); i++)
if (arr[i] == sum)res++;
stacks.push(root);
root = root->left ? root->left : root->right;
}
root = stacks.top();
stacks.pop();
//回退
arr.pop_back();
for (int i = 0; i < arr.size(); i++)
arr[i] = arr[i] - root->val;
if (!stacks.empty() && stacks.top()->left == root)
root = stacks.top()->right;
else
root = nullptr;
}
return res;
}
};
