[数据结构与算法]Strassen矩阵乘法(C++)

思路

两个矩阵A,B相乘时.有以下三种方法

暴力计算法. 三个for循环, 这时候时间复杂度为O(n^3).因为Cij=∑(k=1->n)Aik*Bkj,需要一个循环, 且C中有n^2个元素, 所以时间复杂度为O(n^3)

分治法. 首先将A,B,C分成相等大小的方块矩阵.

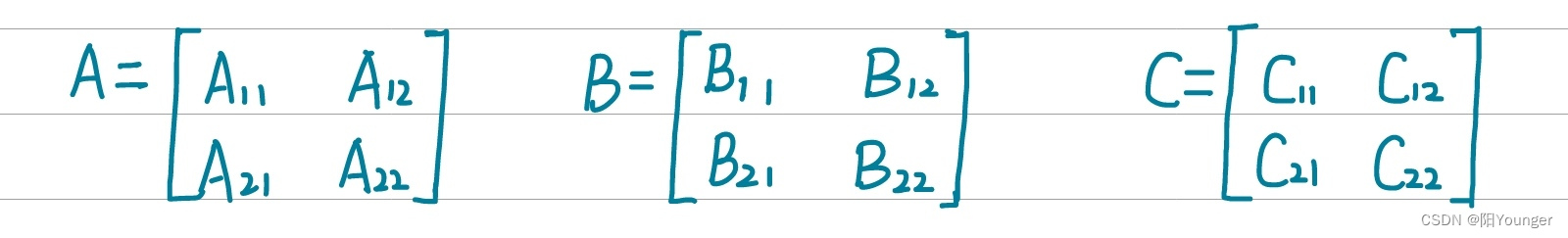
所以C11=A11*B11+A12*B21, C12=A11*B12+A12*B22,

C21=A21*B11+A22*B21, C22=A21*B12+A22*B22

用T(n)表示n*n矩阵的乘法, 所以有T(n)=8T(n/2)+Θ(n^2). 其中, 8T(n/2)表示8次子矩阵乘法, 子矩阵的规模为n/2 * n/2. θ(n^2)表示4次矩阵加法的时间复杂度以及合并C矩阵的时间复杂度.最后结果是Θ(n^3)与暴力计算时间复杂度相同.

Strassen算法,可以将时间复杂度优化到O(n^log7).

现在重新定义7个新矩阵

M1=(A11+A22)*(B11+B22)

M2=(A21+A22)*B11

M3=A11*(B12-B22)

M4=A22*(B21-B11)

M5=(A11+A12)*B22

M6=(A21-A11)*(B11+B12)

M7=(A12-A22)*(B21+B22)

结果矩阵C可以组合上述矩阵,如下

C11=M1+M4-M5+M7

C12=M3+M5

C21=M2+M4

C22=M1-M2+M3+M6

这时候共用了7次乘法,18次加减法运算. 写出递推公式T(n)=7T(n/2)+Θ(n^2). 最终结果是O(n^log7)=O(n^2.807).

代码如下:

#include <bits/stdc++.h>

using namespace std;

// 矩阵相乘的暴力求解
void MUL(int** MatrixA,int** MatrixB,int** MatrixResult,int Msize){
    for(int i=0;i<Msize;i++){
        for(int j=0;j<Msize;j++){
            MatrixResult[i][j]=0;
            for(int k=0;k<Msize;k++){
                MatrixResult[i][j]+=MatrixA[i][k]*MatrixB[k][j];
            }
        }
    }
}

// 矩阵相加运算
void ADD(int** MatrixA,int** MatrixB,int** MatrixResult,int Msize){
    for(int i=0;i<Msize;i++){
        for(int j=0;j<Msize;j++){
            MatrixResult[i][j]=MatrixA[i][j]+MatrixB[i][j];
        }
    }
}

// 矩阵相减运算
void SUB(int** MatrixA,int** MatrixB,int** MatrixResult,int Msize){
    for(int i=0;i<Msize;i++){
        for(int j=0;j<Msize;j++){
            MatrixResult[i][j]=MatrixA[i][j]-MatrixB[i][j];
        }
    }
}

// Strassen算法
void Strassen(int N,int** MatrixA,int** MatrixB,int** MatrixC){
    int halfSize=N/2;
    if(N<=2){
        MUL(MatrixA,MatrixB,MatrixC,N);
    }
    else{
        // 创建二维数组指针
        int** A11;
        int** A12;
        int** A21;
        int** A22;

        int** B11;
        int** B12;
        int** B21;
        int** B22;

        int** C11;
        int** C12;
        int** C21;
        int** C22;

        int** M1;
        int** M2;
        int** M3;
        int** M4;
        int** M5;
        int** M6;
        int** M7;
        int** AResult;
        int** BResult;
        // 初始化
        A11=new int*[halfSize];
        A12=new int*[halfSize];
        A21=new int*[halfSize];
        A22=new int*[halfSize];

        B11=new int*[halfSize];
        B12=new int*[halfSize];
        B21=new int*[halfSize];
        B22=new int*[halfSize];

        C11=new int*[halfSize];
        C12=new int*[halfSize];
        C21=new int*[halfSize];
        C22=new int*[halfSize];

        M1=new int*[halfSize];
        M2=new int*[halfSize];
        M3=new int*[halfSize];
        M4=new int*[halfSize];
        M5=new int*[halfSize];
        M6=new int*[halfSize];
        M7=new int*[halfSize];
        AResult=new int*[halfSize];
        BResult=new int*[halfSize];

        for(int i=0;i<halfSize;i++){
            A11[i]=new int[halfSize];
            A12[i]=new int[halfSize];
            A21[i]=new int[halfSize];
            A22[i]=new int[halfSize];

            B11[i]=new int[halfSize];
            B12[i]=new int[halfSize];
            B21[i]=new int[halfSize];
            B22[i]=new int[halfSize];

            C11[i]=new int[halfSize];
            C12[i]=new int[halfSize];
            C21[i]=new int[halfSize];
            C22[i]=new int[halfSize];

            M1[i]=new int[halfSize];
            M2[i]=new int[halfSize];
            M3[i]=new int[halfSize];
            M4[i]=new int[halfSize];
            M5[i]=new int[halfSize];
            M6[i]=new int[halfSize];
            M7[i]=new int[halfSize];

            AResult[i]=new int[halfSize];
            BResult[i]=new int[halfSize];
        }

        // 把MatrixA和MatrixB分块
        for(int i=0;i<N/2;i++){
            for(int j=0;j<N/2;j++){
                A11[i][j]=MatrixA[i][j];
                A12[i][j]=MatrixA[i][j+N/2];
                A21[i][j]=MatrixA[i+N/2][j];
                A22[i][j]=MatrixA[i+N/2][j+N/2];

                B11[i][j]=MatrixB[i][j];
                B12[i][j]=MatrixB[i][j+N/2];
                B21[i][j]=MatrixB[i+N/2][j];
                B22[i][j]=MatrixB[i+N/2][j+N/2];
            }
        }

        // M1=(A11+A22)*(B11+B22)
        ADD(A11,A22,AResult,halfSize);
        ADD(B11,B22,BResult,halfSize);
        Strassen(halfSize,AResult,BResult,M1);

        // M2=(A21+A22)*B11
        ADD(A21,A22,AResult,halfSize);
        Strassen(halfSize,AResult,B11,M2);

        // M3=A11*(B12-B22)
        SUB(B12,B22,BResult,halfSize);
        Strassen(halfSize,A11,BResult,M3);

        // M4=A22*(B21-B11)
        SUB(B21,B11,BResult,halfSize);
        Strassen(halfSize,A22,BResult,M4);

        // M5=(A11+A12)B22
        ADD( A11, A12, AResult, halfSize);
        Strassen(halfSize, AResult, B22, M5);

        // M6=(A21-A11)*(B11+B12)
        SUB( A21, A11, AResult, halfSize);
        ADD( B11, B12, BResult, halfSize);
        Strassen( halfSize, AResult, BResult, M6);

        // M7=(A12-A22)*(B21+B22)
        SUB(A12, A22, AResult, halfSize);
        ADD(B21, B22, BResult, halfSize);
        Strassen(halfSize, AResult, BResult, M7);

        // C11=M1+M4-M5+M7
        ADD( M1, M4, AResult, halfSize);
        SUB( M7, M5, BResult, halfSize);
        ADD( AResult, BResult, C11, halfSize);

        // C12=M3+M5
        ADD( M3, M5, C12, halfSize);

        // C21=M2+M4
        ADD( M2, M4, C21, halfSize);

        // C22=M1-M2+M3+M6
        ADD( M1, M3, AResult, halfSize);
        SUB( M6, M2, BResult, halfSize);
        ADD( AResult, BResult, C22, halfSize);

        // 把C11,C12,C21,C22矩阵合并成一个大矩阵MatrixC
        for(int i=0;i<N/2;i++){
            for(int j=0;j<N/2;j++){
                MatrixC[i][j]=C11[i][j];
                MatrixC[i][j+N/2]=C12[i][j];
                MatrixC[i+N/2][j]=C21[i][j];
                MatrixC[i+N/2][j+N/2]=C22[i][j];
            }
        }

        // 释放空间
        for (int i = 0; i < halfSize; i++)
        {
            delete[] A11[i];delete[] A12[i];delete[] A21[i];
            delete[] A22[i];

            delete[] B11[i];delete[] B12[i];delete[] B21[i];
            delete[] B22[i];
            delete[] C11[i];delete[] C12[i];delete[] C21[i];
            delete[] C22[i];
            delete[] M1[i];delete[] M2[i];delete[] M3[i];delete[] M4[i];
            delete[] M5[i];delete[] M6[i];delete[] M7[i];
            delete[] AResult[i];delete[] BResult[i] ;
        }
        delete[] A11;delete[] A12;delete[] A21;delete[] A22;
        delete[] B11;delete[] B12;delete[] B21;delete[] B22;
        delete[] C11;delete[] C12;delete[] C21;delete[] C22;
        delete[] M1;delete[] M2;delete[] M3;delete[] M4;delete[] M5;
        delete[] M6;delete[] M7;
        delete[] AResult;
        delete[] BResult;
    }

}

int main()
{
    int MSize;
    cin >> MSize;

    // 定义三个矩阵
    int** MatrixA;
    int** MatrixB;
    int** MatrixC;

    // 初始化三个矩阵
    MatrixA=new int*[MSize];
    MatrixB=new int*[MSize];
    MatrixC=new int*[MSize];
    for(int i=0;i<MSize;i++){
        MatrixA[i]=new int[MSize];
        MatrixB[i]=new int[MSize];
        MatrixC[i]=new int[MSize];
    }

    // 输入相乘的矩阵
    for(int i=0;i<MSize;i++){
        for(int j=0;j<MSize;j++){
            cin >> MatrixA[i][j];
        }
    }
    for(int i=0;i<MSize;i++){
        for(int j=0;j<MSize;j++){
            cin >> MatrixB[i][j];
        }
    }

    Strassen(MSize,MatrixA,MatrixB,MatrixC);

    // 打印输出结果矩阵
    for(int i=0;i<MSize;i++){
        for(int j=0;j<MSize;j++){
            cout << MatrixC[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}


/* 一组数据
4
1 2 4 7
8 3 6 5
4 7 2 1
6 4 3 1
1 2 4 7
8 3 6 5
4 7 2 1
6 4 3 1
*/

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖