顺/逆时针旋转矩阵?

?题目很好理解,就是让你将一个二维矩阵顺时针旋转 90 度,难点在于要「原地」修改,函数签名如下
void rotate(int[][] matrix)
如何「原地」旋转二维矩阵?稍想一下,感觉操作起来非常复杂,可能要设置巧妙的算法机制来「一圈一圈」旋转矩阵:
但实际上,这道题不能走寻常路,在讲巧妙解法之前,我们先看另一道谷歌曾经考过的算法题热热身:
给你一个包含若干单词和空格的字符串?s,请你写一个算法,原地反转所有单词的顺序。
比如说,给你输入这样一个字符串:
s = "hello world labuladong"
你的算法需要原地反转这个字符串中的单词顺序:
s = "labuladong world hello"
常规的方式是把?s?按空格?split?成若干单词,然后?reverse?这些单词的顺序,最后把这些单词?join?成句子。但这种方式使用了额外的空间,并不是「原地反转」单词。
正确的做法是,先将整个字符串?s?反转:
s = "gnodalubal dlrow olleh"
然后将每个单词分别反转:
s = "labuladong world hello"
这样,就实现了原地反转所有单词顺序的目的。
我讲这道题的目的是什么呢?
旨在说明,有时候咱们拍脑袋的常规思维,在计算机看来可能并不是最优雅的;但是计算机觉得最优雅的思维,对咱们来说却不那么直观。也许这就是算法的魅力所在吧。
回到之前说的顺时针旋转二维矩阵的问题,常规的思路就是去寻找原始坐标和旋转后坐标的映射规律,但我们是否可以让思维跳跃跳跃,尝试把矩阵进行反转、镜像对称等操作,可能会出现新的突破口。
我们可以先将?n x n?矩阵?matrix?按照左上到右下的对角线进行镜像对称:
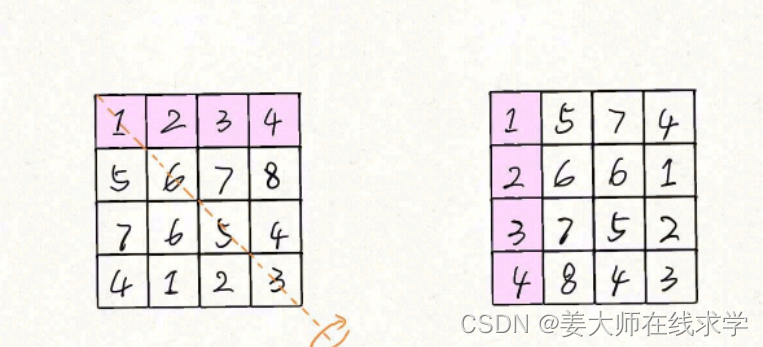
?然后再对矩阵的每一行进行反转
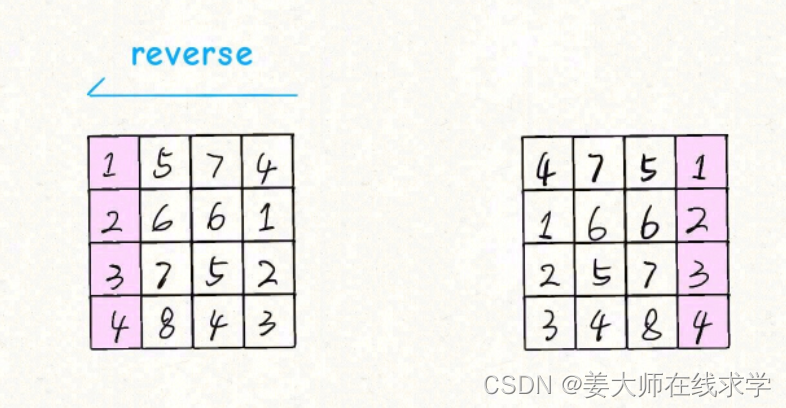
?发现结果就是?matrix?顺时针旋转 90 度的结果
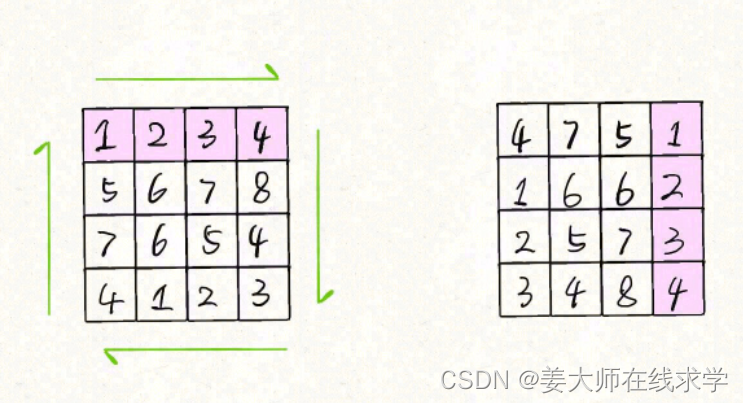
将上述思路翻译成代码,即可解决本题?
// 将二维矩阵原地顺时针旋转 90 度
public void rotate(int[][] matrix) {
int n = matrix.length;
// 先沿对角线镜像对称二维矩阵
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
// swap(matrix[i][j], matrix[j][i]);
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
// 然后反转二维矩阵的每一行
for (int[] row : matrix) {
reverse(row);
}
}
// 反转一维数组
void reverse(int[] arr) {
int i = 0, j = arr.length - 1;
while (j > i) {
// swap(arr[i], arr[j]);
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
肯定有读者会问,如果没有做过这道题,怎么可能想到这种思路呢?
仔细想想,旋转二维矩阵的难点在于将「行」变成「列」,将「列」变成「行」,而只有按照对角线的对称操作是可以轻松完成这一点的,对称操作之后就很容易发现规律了。
既然说道这里,我们可以发散一下,如何将矩阵逆时针旋转 90 度呢?
思路是类似的,只要通过另一条对角线镜像对称矩阵,然后再反转每一行,就得到了逆时针旋转矩阵的结果: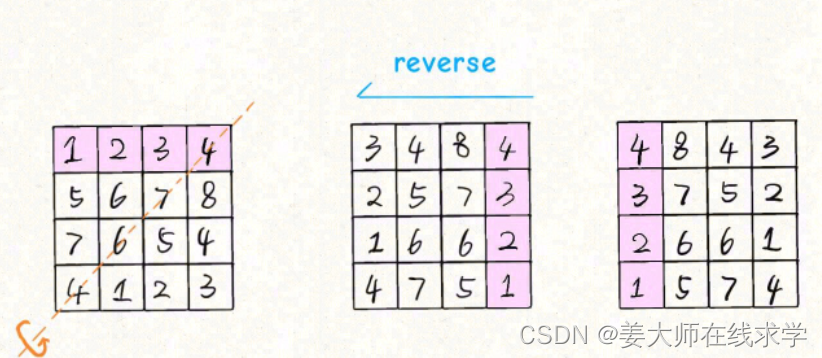
// 将二维矩阵原地逆时针旋转 90 度
void rotate2(int[][] matrix) {
int n = matrix.length;
// 沿左下到右上的对角线镜像对称二维矩阵
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - i; j++) {
// swap(matrix[i][j], matrix[n-j-1][n-i-1])
int temp = matrix[i][j];
matrix[i][j] = matrix[n - j - 1][n - i - 1];
matrix[n - j - 1][n - i - 1] = temp;
}
}
// 然后反转二维矩阵的每一行
for (int[] row : matrix) {
reverse(row);
}
}
void reverse(int[] arr) { /* 见上文 */}
?矩阵的螺旋遍历
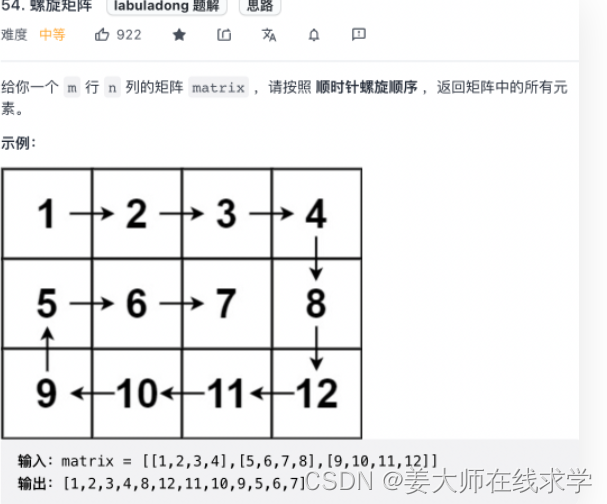
解题的核心思路是按照右、下、左、上的顺序遍历数组,并使用四个变量圈定未遍历元素的边界
?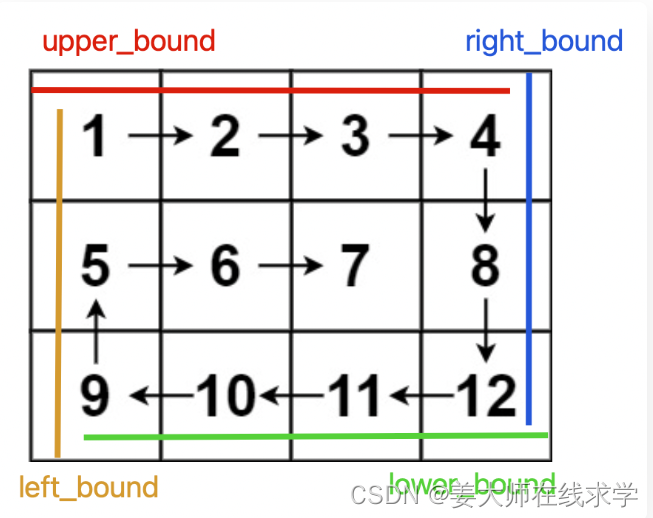
?随着螺旋遍历,相应的边界会收缩,直到螺旋遍历完整个数组:
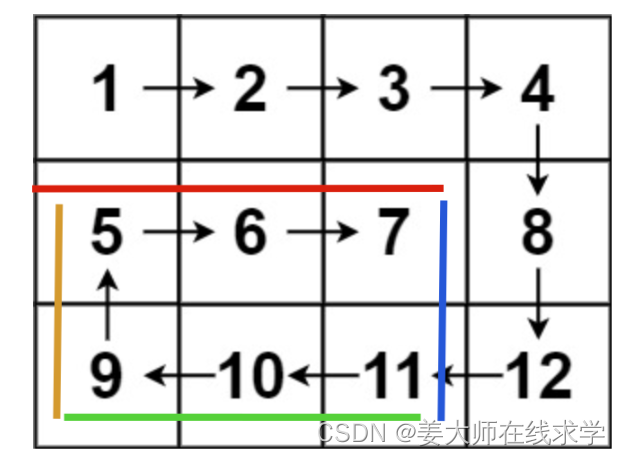
只要有了这个思路,翻译出代码就很容易了?
List<Integer> spiralOrder(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
int upper_bound = 0, lower_bound = m - 1;
int left_bound = 0, right_bound = n - 1;
List<Integer> res = new LinkedList<>();
// res.size() == m * n 则遍历完整个数组
while (res.size() < m * n) {
if (upper_bound <= lower_bound) {
// 在顶部从左向右遍历
for (int j = left_bound; j <= right_bound; j++) {
res.add(matrix[upper_bound][j]);
}
// 上边界下移
upper_bound++;
}
if (left_bound <= right_bound) {
// 在右侧从上向下遍历
for (int i = upper_bound; i <= lower_bound; i++) {
res.add(matrix[i][right_bound]);
}
// 右边界左移
right_bound--;
}
if (upper_bound <= lower_bound) {
// 在底部从右向左遍历
for (int j = right_bound; j >= left_bound; j--) {
res.add(matrix[lower_bound][j]);
}
// 下边界上移
lower_bound--;
}
if (left_bound <= right_bound) {
// 在左侧从下向上遍历
for (int i = lower_bound; i >= upper_bound; i--) {
res.add(matrix[i][left_bound]);
}
// 左边界右移
left_bound++;
}
}
return res;
}

?有了上面的铺垫,稍微改一下代码即可完成这道题:
int[][] generateMatrix(int n) {
int[][] matrix = new int[n][n];
int upper_bound = 0, lower_bound = n - 1;
int left_bound = 0, right_bound = n - 1;
// 需要填入矩阵的数字
int num = 1;
while (num <= n * n) {
if (upper_bound <= lower_bound) {
// 在顶部从左向右遍历
for (int j = left_bound; j <= right_bound; j++) {
matrix[upper_bound][j] = num++;
}
// 上边界下移
upper_bound++;
}
if (left_bound <= right_bound) {
// 在右侧从上向下遍历
for (int i = upper_bound; i <= lower_bound; i++) {
matrix[i][right_bound] = num++;
}
// 右边界左移
right_bound--;
}
if (upper_bound <= lower_bound) {
// 在底部从右向左遍历
for (int j = right_bound; j >= left_bound; j--) {
matrix[lower_bound][j] = num++;
}
// 下边界上移
lower_bound--;
}
if (left_bound <= right_bound) {
// 在左侧从下向上遍历
for (int i = lower_bound; i >= upper_bound; i--) {
matrix[i][left_bound] = num++;
}
// 左边界右移
left_bound++;
}
}
return matrix;
}
以上就是遍历二维数组的一些技巧
