前言

hello，大家好，接下来博主将会推出一系列算法刷题的博文，欢迎大家继续支持博主。今天我们来做第一道题：Bridge。

1. 题目描述

n个人要在晚上过桥，任何时候最多两人一组过桥，每组要有一只手电筒。在这n个人中只有一只手电筒可以用，因此要安排以某种往返的方式来返还手电筒，使得更多的人可以过桥。
每个人的过桥速度不同，每组的速度由速度较慢的成员所决定。请确定一个策略，使得n个人用最少的时间过桥。
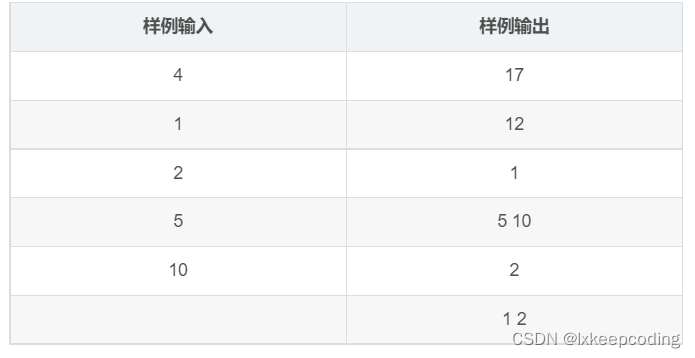
输入
输人的第一行给出n，接下来的n行给出每个人的过桥时间，不会超过1000人，且没有人的过桥时间超过100秒。
输出
输出的第一行给出所有n个人过桥的总秒数，接下来的若干行给出实现策略。每行包含一个或两个整数，表示组成一组过桥的一个人或两个人(每个人用其在输人中给出的过桥所用的时间来标识。虽然许多人有相同的过桥时间，但即使有混淆，对结果也没有影响)。这里要注意的是过桥也有方向性，因为要返还手电筒让更多的人通过。如果用时最少的策略有多个，则任意一个都可以。

2. 试题分析

在研究这道问题时，我们可以确定一个这样的基本思想，要使时间最短，则慢的成员必须借助快的成员传递手电筒。一次过桥最多两个人并且手电筒需要往返。
我们用每个人的过桥时间表示这个人，按照过桥时间递增顺序排列，我们设这个序列：
A为最快的人，B为次快的人，C为第三快的人。A、B是序列首部的两个元素。
a为最慢的人，b为次慢的人，a、b是序列尾部的两个元素。

如果我们让a和b用最短的时间过桥，则我们可以有以下两种考虑。

1 .由A带过河，A先带a，用时a，A回返，用时A，然后带B用时b，然后A回返。即由A带a、b过河用时为T1=2*A+a+b。

2 . 用A和B传递手电筒，帮助a和b过河。首先A、B到对岸，用时为B。A返回，将手电筒给a、b，a、b过河，用时为a。然后将手电筒给B，B返回将手电筒交还给A,用时为B。即由A和B带领a、b过河的时间为T2=2*B+A+a。

很明显，如果a、 b要用最少的时间过河，只能借助A或者A、B传递手电筒。如果T1<T2则采取1.反之则采取2。
我们每次帮助最慢和次慢的两个成员过河（n-=2）。最后，会出现如下两种情况：
1.对岸剩下2个队员（两个队员为A和B，用时为B）
2.对岸剩下3个队员（三个队员为A、B、C，用时为A+B+C）

3. 代码实现

#include<iostream>
#include<algorithm>

using namespace std;

int n,a[111111];          
int ans = 0;               

int main()
{
	cin >> n;
	for (int i = 1; i <=n; i++)
	{
		cin >> a[i];
	}
	if (n == 1)            
	{
		cout << a[1] << endl;
		cout << a[1] << endl;
	}
	int nn = n;
	sort(a + 1, a + n + 1);
	while (n > 3)
	{
		if (a[1] + a[n - 1] < 2 * a[2])
		{
			ans += a[n] + a[1] * 2 + a[n - 1];
		}
		else
		{
			ans += a[2] + a[1] + a[2] + a[n];
		}
		n -= 2;
	}
	if (n == 2)
	{
		ans += a[2];
	}
	else
	{
		ans += a[1] + a[2] + a[3];
	}
	cout << ans << endl;
	n = nn;
	while (n > 3)
	{
		if (a[1] + a[n - 1] < 2 * a[2])
		{
			cout << a[1] << "  " << a[n]
				<< endl << a[1] << endl << a[1] 
				<< "  " << a[n - 1] << endl << a[1] << endl;
		}
		else
		{
			cout << a[1] << "  " << a[2]
				<< endl << a[1] << endl << a[n - 1] 
				<< "  " << a[n] << endl << a[2] << endl;
		}
		n -= 2;
	}
	if (n == 2)
	{
		cout << a[1] << "  " << a[2] << endl;
	}
	else
	{
		cout << a[1] << "  " << a[3] << endl << a[1] << endl << a[1] << "  " << a[2];
	}
	return 0;
}