更快更高更强

路径压缩

细心的同学可以已经注意到了，上一章节的最后一个题目的代码出现了路径压缩这个东西，这里就来说说怎么让并查集更加健壮。

首先来说，原先的查找过程中可以看到是一个循环向前查询的过程，但是如果情况比较糟糕，最终的结构搞成了一字长蛇阵，那么查询效果就会不尽如人意，所以有无办法优化呢，其实可以在查询到最终结果时将路径上的所有节点的直接上级改成查询出的最终上级，并查集构造过程中不断优化现有结构，就会得到一个比较优秀的查询结果，从数据结构的角度来看—维护的树深度缩短了。这就是路径压缩。

//查找祖先的操作
int findAncestor(int x) { //寻找节点X的祖先
    int originX = x;
    while(x != faction[x]) {
        x = faction[x];
    }

    //路径压缩
    while(originX != faction[originX]) {
        originX = faction[originX];
        faction[originX] = x;
    }
    return x;
}

按秩合并

上面的路径压缩优化了查找的过程，合并的过程其实也能提升下，前面提到了，合并过程，现在是随便合并的，但实际上，如果是下面的这种情况

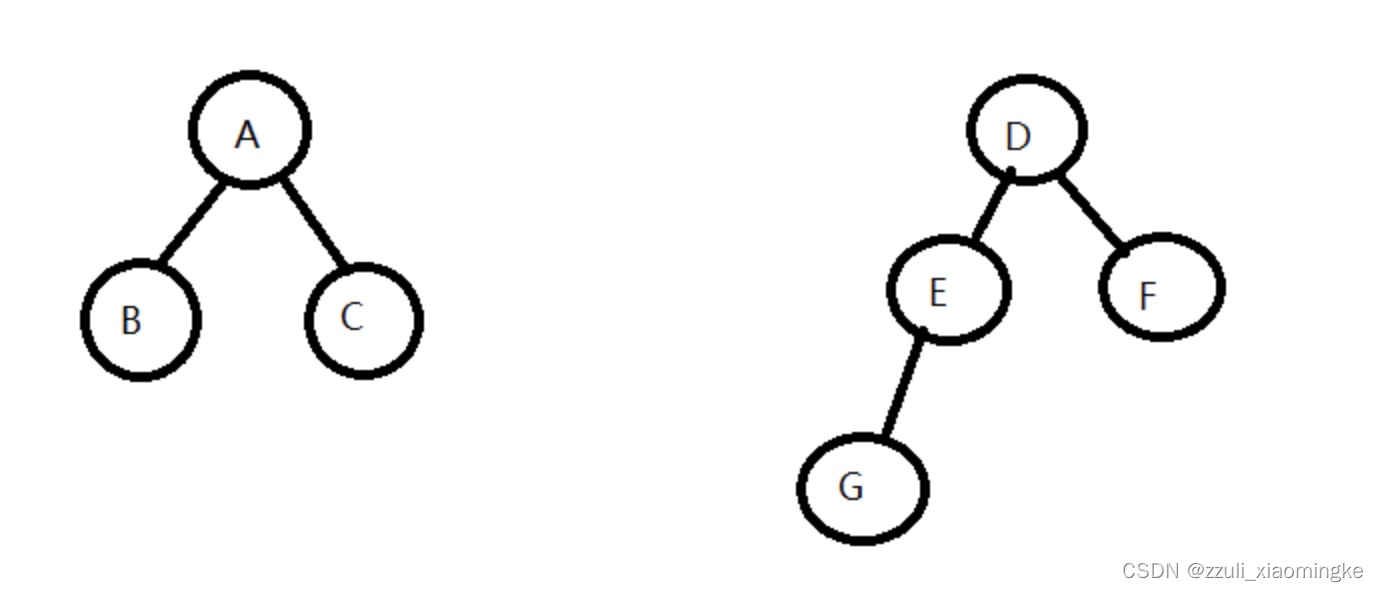
请添加图片描述

遇到这种情况，我们更希望能够把左边元素集合并入右边，也就是把深度较小的连通分量并入深度较大的连通分量，因为深度较大的连通分量元素较多，如果并入其他连通分量，深度更大，查询起来压力不小，所以可以单独维护一个深度数组depth[i] = x，表示节点i所在连通分量树的深度为x，在合并操作的时候，就能够确定谁去合并谁了。

int faction[30005]; //标记节点的祖先节点
//合并两个节点所在的派系
void unionFaction(int x, int y) {
    int AneX = findAncestor(x);
    int AneY = findAncestor(y);
    faction[AneX] = AneY;
    if(depth[AneX] > depth[AneY]) { //如果x所在树的深度较大
        faction[AneY] = AneX; 
    }else {
        if(depth[AneX] == depth[AneY]) { //如果x和y的层高相同的话，合并后新层高加1
            depth[AneY]++;
        }
        faction[AneX] = AneY; 
    }
}