二维区域和检索-矩阵不可变的思路探讨与源码
????二维区域和检索-矩阵不可变的题目如下图,该题属于数学类和矩阵类型的题目,主要考察对于矩阵搜索方法的使用和题目本身思路的理解。本文的题目作者想到2种方法,分别是前缀和方法和动态规划方法,其中前缀和方法使用Java进行编写,而动态规划方法使用Python进行编写,当然这可能不是最优的解法,还希望各位大佬给出更快的算法。

????本人认为该题目可以使用前缀和方法的思路进行解决,首先计算矩阵的长度,如果矩阵长度大于0就计算矩阵的宽度,初始化一个数组,长宽都比原有的矩阵大1,开始循环遍历矩阵,将矩阵的每一个元素按照公式进行重新计算,最终直到遍历结束。那么按照这个思路我们的Java代码如下:
#喷火龙与水箭龟
class NumMatrix {
int[][] mat;
public NumMatrix(int[][] arr) {
int arrLen = arr.length;
if (arrLen > 0) {
int arrNum = arr[0].length;
mat = new int[arrLen + 1][arrNum + 1];
for (int ir = 0; ir < arrLen; ir++) {
for (int jr = 0; jr < arrNum; jr++) {
mat[ir+1][jr+1]=mat[ir][jr+1]+mat[ir+1][jr]-mat[ir][jr]+arr[ir][jr];
}
}
}
}
public int sumRegion(int r1, int c1, int r2, int c2) {
return mat[r2+1][c2+1]-mat[r1][c2+1]-mat[r2+1][c1]+mat[r1][c1];
}
}

????显然,我们看到前缀和方法的效果比较好,同时还可以使用动态规划的方法解决。首先判断矩阵是否为空,如果非空就计算矩阵的长和宽,并且初始化一个比原矩阵长和宽都大1的动态规划矩阵,然后开始遍历矩阵,矩阵的每个子范围的元素都加到动态规划矩阵的结果里。遍历动态规划矩阵,将动态规划的每一行的结果都进行求和,按照这个思路得到的结果就是最终结果。所以按照这个思路就可以解决,下面是Python代码:
#喷火龙与水箭龟
class NumMatrix:
def __init__(self, matrix: List[List[int]]):
if(not matrix or not matrix[0]):
pass
else:
r = len(matrix)
c = len(matrix[0])
self.dpArr = [[ 0 ] * (c + 1) for _ in range(r + 1)]
for iz in range(1, r + 1):
for jz in range(1 ,c + 1):
self.dpArr[iz][jz] = self.dpArr[iz][jz - 1] + matrix[iz - 1][jz - 1]
for jb in range(1, c + 1):
for ib in range(1, r + 1):
self.dpArr[ib][jb] += self.dpArr[ib - 1][jb]
def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
return self.dpArr[row2 + 1][col2 + 1] - self.dpArr[row1][col2 + 1] - self.dpArr[row2 + 1][col1] + self.dpArr[row1][col1]
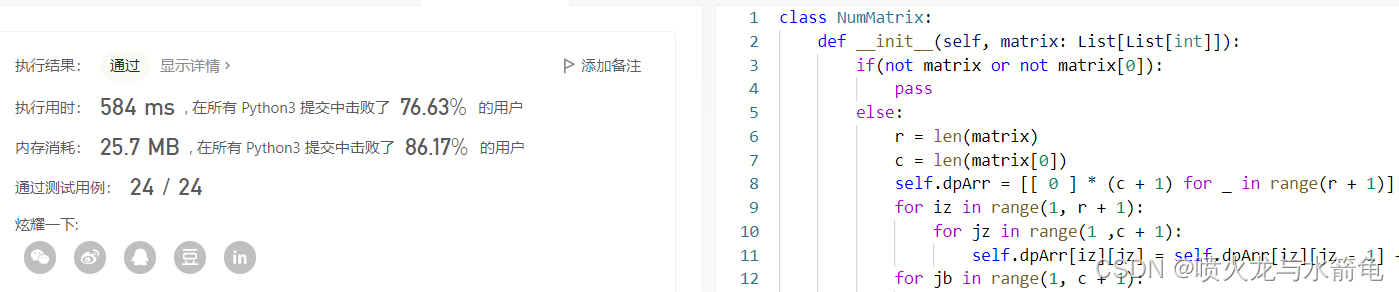
????从结果来说Java版本的前缀和方法的效率比较好,而Python版本的动态规划方法的速度比较一般,但应该是有更多的方法可以进一步提速的,希望朋友们能够多多指教,非常感谢。
