[数据结构与算法]LeetCode 1552、两球之间的磁力

1552、两球之间的磁力

1）题目描述

在代号为 C-137 的地球上，Rick 发现如果他将两个球放在他新发明的篮子里，它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子，第 i 个篮子的位置在 position[i] ，Morty 想把 m 个球放到这些篮子里，使得任意两球间 最小磁力 最大。

已知两个球如果分别位于 x 和 y ，那么它们之间的磁力为 |x - y| 。

给你一个整数数组 position 和一个整数 m ，请你返回最大化的最小磁力。

示例 1：

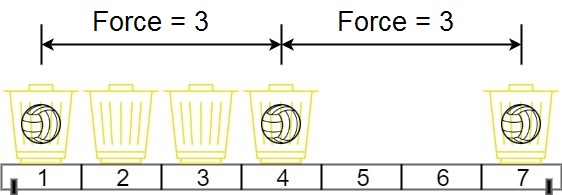
输入：position = [1,2,3,4,7], m = 3
输出：3
解释：将 3 个球分别放入位于 1，4 和 7 的三个篮子，两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。

示例 2：

输入：position = [5,4,3,2,1,1000000000], m = 2
输出：999999999
解释：我们使用位于 1 和 1000000000 的篮子时最小磁力最大。

提示：

• n == position.length
• 2 <= n <= 10^5
• 1 <= position[i] <= 10^9
• 所有 position 中的整数 互不相同 。
• 2 <= m <= position.length

2）分析

二分：

• 球之间的距离代表了磁力，本题实际上是要求球之间的最小距离的最大值；
• 对篮子的位置数组position进行排序；
• 球之间的最小距离最小取值为1，最大取值为篮子位置排序之后的第一个位置和最后一个位置的距离；
• 当球的最小距离取了最大取值之后，若球的数量超过两个，那么久放不下这么多的球；
• 需要在 $[1,最大取值]$ 内寻找一个合适的值，使得最值距离的取值最大，并且还能够放下所有的球，可以使用二分法来寻找；
• 判断在当前取值下是否能够放得下所有的球，第一个球一定是放在第一个篮子内，将剩下的球逐个放入距离当前篮子不小于当前取值的篮子中，若到最后一个篮子的时候，放球数量不小于给定球的数量，表明当前取值下能够放得下所有的球。

3）C++代码

class Solution {
public:
    bool isSuitable(vector<int> position,int minDis,int m){
        int cnt=1;
        int prePos=position[0];
        for(int i=1;i<position.size();i++){
            if(position[i]-prePos>=minDis){
                cnt++;
                prePos=position[i];
            }
        }
        return cnt>=m;
    }

    int maxDistance(vector<int>& position, int m) {
        int n=position.size();
        sort(position.begin(),position.end());
        int left=1;
        int right=position[n-1]-position[0];
        while(left<=right){
            int mid=(right-left)/2+left;
            if(isSuitable(position,mid,m))
                left=mid+1;
            else
                right=mid-1;
        }
        return right;
    }
};

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖