目录
1递归遍历二叉树
1. 1 前序遍历:递归法
-
144.二叉树的前序遍历(中序和后序差不多)
-
思路介绍:
1)首先写主函数
2)然后开始写递归函数(包含两部分,截止条件和递归次序:中间左边右边)
//前序遍历
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList();
//调用递归函数
preorder(root , list);
return list;
}
public static void preorder(TreeNode root,List<Integer> list){
//1)截止条件
if(root==null) return;
//2)操作
list.add(root.val);
//3)递归函数
preorder(root.left,list);
preorder(root.right,list);
}
}
1. 2 前序遍历:迭代法(深度优先算法)
- 思路
1)前序遍历的顺序中左右,那么只需要把入栈的顺序改为中-右-左即可。这样出栈顺序就是中-左-右了
2)代码书写过程类似层序遍历,
(1):定义集合和栈
(2):把首节点放进去
(3):开始进行遍历操作,一层while循环,然后就是先出栈后压栈(顺序为中右边左边) - 代码
//前序遍历
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
//方法二:迭代解法
//1)定义集合和栈
List<Integer> list=new ArrayList<>();
ArrayDeque<TreeNode> deque=new ArrayDeque<>();
//2)特殊情况
if(root==null) return list;
deque.push(root);
//3)进行循环
while(deque.size()>0){
//先删除父节点,然后判断压入子节点(从右到左)
TreeNode fa=deque.pop();
list.add(fa.val);
if(fa.right!=null) deque.push(fa.right) ;
if(fa.left!=null) deque.push(fa.left) ;
}
//4)返回结果
return list;
}
}
//后续遍历
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
//迭代方法
//需要的结果是左右中,可以先做出来中右左-反转得到左右中
//为了得到中右左,故压栈的顺序为中左右
//1)集合和栈的定义
List<Integer> list=new ArrayList<>();
ArrayDeque<TreeNode> deque=new ArrayDeque<>();
//2)特殊情况
if(root==null) return list;
deque.push(root);
//3)开始循环遍历
while(deque.size()>0){
TreeNode temp=deque.pop();
list.add(temp.val); //中间
if(temp.left!=null) deque.push(temp.left);
if(temp.right!=null) deque.push(temp.right);
}
//4)进行反转
Collections.reverse(list);
return list;
}
}
1. 3 层序遍历:迭代法
- 思路步骤
1) 定义二维数组集合与队列
2)特殊情况先考虑,并把根节点放进去
3)根节点不为空,那么就一层一层放东西(两层while循环)
(1)第一层while循环,得到目前队列的大小,判断是否还有下一层,然后把上一层的数据装载入集合中
(2) 第二层while循环,(先存子节点,和父节点值,再删父节点)循环遍历队列中的元素,看子节点是否存在,存在就进行输入队列,然后把父节点值存入,再删除父节点。
(3)在第一层里,第二层外,把每一层的数据存起来。
4)输出二维集合数据 - 代码展示
public List<List<Integer>> levelOrder(TreeNode root) {
//1)新建集合和队列
List<List<Integer>> data=new ArrayList<>();
ArrayDeque<TreeNode> deque=new ArrayDeque<>();
//特殊情况
if(root==null) return data;
deque.offer(root);
//3)两层while循环
int size;
while(deque.size()!=0){
//(1)新建一维集合装数据,计算size的大小,方便二层循环
List<Integer> list=new ArrayList<>();
size=deque.size();
while(size-->0){
//(2)先把数据装进行,然后看子节点是否需要装入队列中
if(deque.peek().left!=null) deque.offer(deque.peek().left);
if(deque.peek().right!=null) deque.offer(deque.peek().right);
list.add(deque.poll().val); //查找的同时进行删除
}
data.add(list);
}
return data;
}
- 总结
1)层序遍历是一个经典的bfs算法(广度搜索算法)。对一个地方都会进行遍历一遍,能够解决很多类似问题
2)能够解决一些类型问题
 3)层序遍历算法是使用迭代法,使用队列装节点。
3)层序遍历算法是使用迭代法,使用队列装节点。
1. 3.1 Leecode:116. 填充每个节点的下一个右侧节点指针
-
题目描述
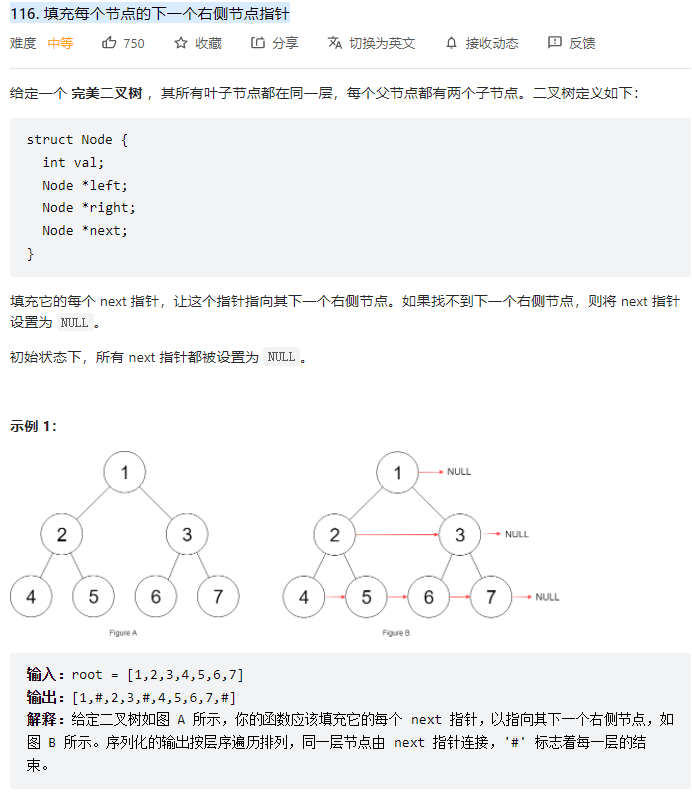
-
思路说明‘
1)需要额外的两个操作
(1):父节点右边节点与相邻节点的左边节点链接
(2):父节点的子节点之间的连接(非空一定有) -
代码展示
class Solution {
//核心思路:如果next没有赋值,默认为null节点
//递归的三部曲:截止条件;操作;递归方向
public Node connect(Node root) {
//1)特殊情况(根节点为空或者子节点不存在)
if(root == null || root.left == null) return root;
//2)根节点存在,子节点存在;连接子节点之间的线
root.left.next = root.right;
//3)如果相邻节点存在子节点,那么这两个节点之间子类的先要连起来。
if(root.next != null) root.right.next = root.next.left;
//4)进行递归遍历
connect(root.left);
connect(root.right);
//5)输出
return root;
}
}
2 反转二叉树

2.1 前序遍历:深搜
class Solution {
public TreeNode invertTree(TreeNode root) {
//前序遍历:递归法
//1)截止条件
if(root==null) return root;
//2)操作
swap(root);
//3)递归
invertTree(root.left);
invertTree(root.right);
return root;
}
public static void swap(TreeNode node){
TreeNode temp=node.left;
node.left=node.right;
node.right=temp;
}
}
2.2 后序遍历:深搜
class Solution {
public TreeNode invertTree(TreeNode root) {
//后序遍历:递归法
//1)截止条件
if(root==null) return root;
//3)递归
invertTree(root.left); //左
invertTree(root.right); //右
//2)操作
swap(root); //中
return root;
}
public static void swap(TreeNode node){
TreeNode temp=node.left;
node.left=node.right;
node.right=temp;
}
}
2.3 层序遍历:广搜
class Solution {
public TreeNode invertTree(TreeNode root) {
//层序遍历:使用
//1)栈的定义
ArrayDeque<TreeNode> deque=new ArrayDeque<>();
//2)特殊情况
if(root==null) return root;
deque.push(root);
//3)循环遍历
while(deque.size()>0){
int size=deque.size();
while(size-->0){
TreeNode node=deque.pop();
swap(node); //中
if(node.left!=null) deque.push(node.left); //左边
if(node.right!=null) deque.push(node.right); //右边
}
}
return root;
}
public static void swap(TreeNode node){
TreeNode temp=node.left;
node.left=node.right;
node.right=temp;
}
}
3 对称二叉树
- 题目描述
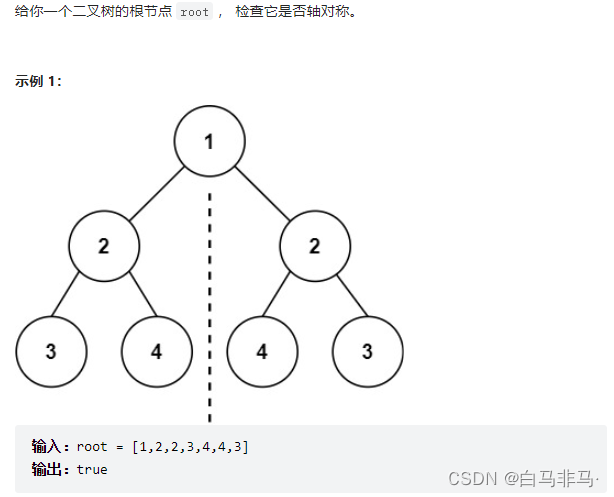
- 思路
1)书写递归方法,输入两个子节点
2)截止条件:判断两个子节点的情况(四种情况,有空值,值不相等)
3)递归:保证两个子节点是相等的,非空的:A:两个子节点的外侧;B:两个子节点的内侧
4)该递归是有返回值的:不满足条件的时候,会立即退出
class Solution {
public boolean isSymmetric(TreeNode root) {
//对称二叉树:使用递归进行书写(后续遍历)
//定义一个方法:一下需要传入两个值
return method(root.left,root.right);
}
public static boolean method(TreeNode node1,TreeNode node2){
//截止条件
if(node1==null && node2==null) return true;
if(node1==null && node2!=null) return false;
if(node2==null && node1!=null) return false;
if(node2.val!=node1.val) return false;
//在node2.val==node1.val情况下判断
//递归:因为有返回值,不需要遍历全局,故要提取返回值
boolean A=method(node1.left, node2.right);
boolean B=method(node1.right, node2.left);
return A && B;
}
}
4 二叉树最大深度
- 概念介绍
1)深度:从根节点到该节点的最长简单路径边(需要从上往下查,一般使用前序遍历)
2)高度:从该节点到叶子节点的最长简单路径边(从下到上查,一般使用后序遍历) - 后序遍历递归算法
class Solution {
public int maxDepth(TreeNode root) {
//使用后序遍历:递归方法
//1)截止条件
if(root==null) return 0;
//2)递归
int A=maxDepth(root.left); //左边
int B=maxDepth(root.right); //右边
return Math.max(A,B)+1; //中间一层加一
}
2. 前序遍历递归算法
5 N叉树最大深度
- 后序遍历递归算法
class Solution {
public int maxDepth(Node root) {
//使用二叉树的后序遍历算法
//
if(root==null) return 0;
int result=0;
for(int i=0;i<root.children.size();i++){
result=Math.max(result,maxDepth(root.children.get(i)));
}
return result+1; //有返回值,那么中间的那一步就丢给return 来完成。
}
}
2. 前序遍历递归算法
6 二叉树最小深度
- 思路
1)其实整体上是延续二叉树最大深度的想法
2)在处理两个子节点,其中一个为空的情况,返回值不为此处的零,而为另一边节点深度+1 - 代码
1)方法一:后序遍历的递归
只是在两个子节点,其中一个为空的情况下,更改下逻辑
class Solution {
public int minDepth(TreeNode root) {
//使用后序遍历的方法求解二叉树的最小深度
//和最大深度不一样的地方:如果两个节点,其中一个节点为空,那么最小为另一个节点深度+1值
//截止条件
if(root==null) return 0;
//2)循环体
int leftDepth=minDepth(root.left); //左
int rightDepth=minDepth(root.right); //右
//中
//子情况一:左边为空
if(root.left==null) return 1+rightDepth; //多了这一步
//子情况二:右边为空
if(root.right==null) return 1+leftDepth; //多了这一步
//子情况三:两边都不为空
return 1+Math.min(leftDepth,rightDepth);
}
}
2)方法二:层序遍历的迭代
需要找到叶子节点,那么就输出该层的高度
在第二层while循环中加入这一句:
if(temp.left==null&&temp.right==null){ //出现叶子节点时候,就输出该层
7. 完全二叉树的节点个数
- 概念说明
1)完全二叉树:
2) - 题目说明
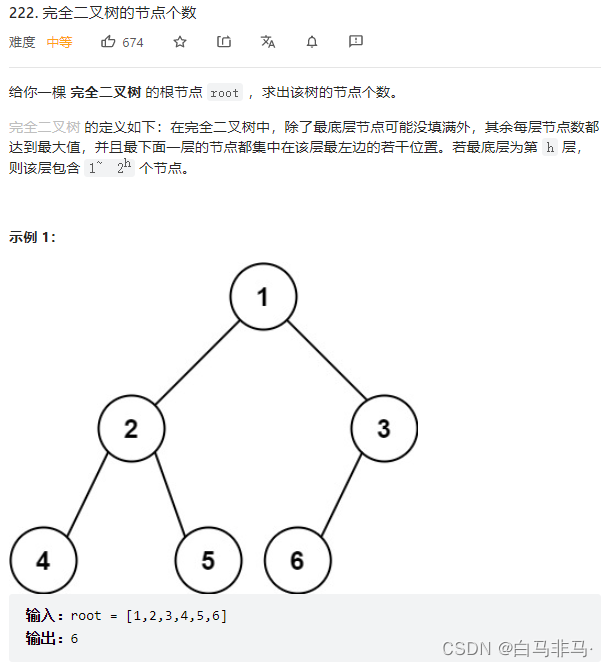
- 思路说明
1)如果把它看成是一个简单的树,那么可以用简单的递归(方法一)
2)通过层序遍历,也可以计算出来(简单树) (方法二)
3)如果看成是完全二叉树,则需要先找到完全二叉树,找到之后用公式,没找到,递归孩子节点用公式。(方法三) - 代码说明
1)方法一:递归,看是一般的树
class Solution {
public int countNodes(TreeNode root) {
//递归,不看成是完全二叉树
//1)截止条件
if(root==null) return 0;
//2)后续遍历递归(先递归,后看状态)
return countNodes(root.left)+countNodes(root.right)+1;
}
}
2)方法二:看成是完全二叉树,通过递归进行求解
class Solution {
public int countNodes(TreeNode root) {
//递归方法(找到完全二叉树,然后用公式计算)
//计算根节点的深度,如果深度相同意味着是满二叉树,即可用公式
//如果深度不同,那么递归左右子树,使用返回左+右+1。
if(root==null) return 0;
TreeNode left=root.left;
TreeNode right=root.right;
int lefthigh=0;
int righthigh=0;
while(left!=null){
left=left.left;
lefthigh++;
}
while(right!=null){
right=right.right;
righthigh++;
}
if(lefthigh==righthigh) {
return (2<<lefthigh)-1; //2左移lefthigh位,即2^(lefthigh+1);
}
return countNodes(root.left)+countNodes(root.right)+1;
}
}
3)方法三:看成是一般的树,通过迭代进行求解
class Solution {
public int countNodes(TreeNode root) {
//方法二:看成是一般的树,通过迭代进行求解
ArrayDeque<TreeNode> deque=new ArrayDeque<>();
//1)截止条件
if(root==null) return 0;
deque.offer(root);
int num=0;
while(deque.size()>0){
int size=deque.size();
while(size-->0){
num++;
TreeNode node=deque.poll();
if(node.left!=null) deque.offer(node.left);
if(node.right!=null) deque.offer(node.right);
}
}
return num;
}
}
8. 平衡二叉树
- 题目说明

- 思路说明
1)代码的核心思路是通过后续遍历,求解树的最大高度
2)核心代码与前一题求取树的最大深度类似
3)在前一题基础上,多加了一些判断,如果节点的左右子树不平衡,就返回-1进行停止。
class Solution {
public boolean isBalanced(TreeNode root) {
//求高度的,使用后序遍历算法
if(gethigh(root)==-1) {
return false;
}else return true;
}
//书写方法
public static int gethigh(TreeNode root){
//1)截止条件
if(root==null) return 0;
//2)递归条件
int lefthigh=gethigh(root.left); //左边
if(lefthigh==-1) return -1;
int righthigh=gethigh(root.right); //右边
if(righthigh==-1) return -1;
//3)中间(判定条件一定是差值大于1) //中间
if(Math.abs(lefthigh-righthigh)>1) return -1;
return Math.max(lefthigh,righthigh)+1;
}
}
9. 二叉树的所有路径(广搜的思想)
-
题目:
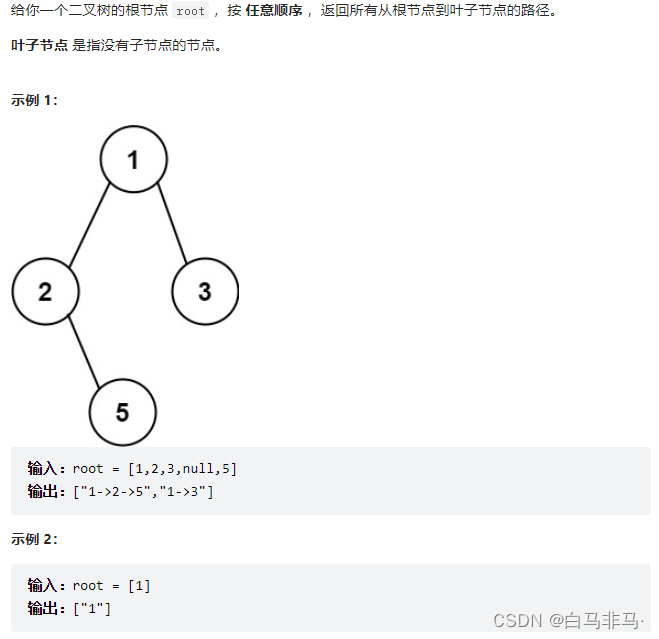
-
思路:
1)使用前序遍历进行全局遍历,因为是搜索全树,满足条件的路径。
2)递归函数的返回值类型和入参: 返回值类型为空(因为要遍历全树),入参为(根节点,String集合存结果,Integer存路径)
3)第一步:把根节点加入Integer集合中
4)(中):如果是根节点,那么就返回路径的全部值
5)(左):左边非空,递归左边,并且再回溯一步(即把最后一个路径值返回)
6)(右):右边非空,递归右边,并且再回溯一步(即把最后一个路径值返回) -
代码
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
//本题目设计到了回溯,因为是遍历路径,所以用前序遍历
//定义一个String类型的集合装结果,定义一个Integer类型集合装每走一步的路径
List<String> result=new ArrayList<>();
List<Integer> path=new ArrayList<>();
if(root==null) return result;
method(root,result,path);
return result;
}
//回溯遍历路径方法
public void method(TreeNode root,List<String> res,List<Integer> path){
//0)添加元素进去
path.add(root.val);
//1)截止条件操作 中间
if(root.left==null &&root.right==null){
StringBuilder sb=new StringBuilder();
for(int i=0;i<path.size();i++){
if(i==path.size()-1){
sb.append(path.get(i));
}else{
sb.append(path.get(i)).append("->");
}
}
res.add(sb.toString());
return; //截止条件
}
//2)递归回溯
if(root.left!=null){ //左边
method(root.left,res,path);
path.remove(path.size()-1); //回溯
}
if(root.right!=null){ //右边
method(root.right,res,path);
path.remove(path.size()-1); //回溯
}
}
}
10. 404. 左叶子之和
- 题目

- 思路
1)好好体会前序遍历的思想,从上往下依次进行遍历,先对头的信息进行处理(暂时不需要直到其叶子节点的值)
2)递归三部曲
(注意,如果直接用这个函数,中间需要一个全局变量,或者写为一个子函数,传入已给变量)
(1):截止条件:根节点为空,给节点没有叶子节点,均会返回0
(2):中:遇到了左叶子节点,那么就把左叶子节点之和给加起来
(3):前序遍历常规的递归操作,左右进行遍历
(4):返回值sum - 代码详解
//结合版本
class Solution {
public int sum=0;
public int sumOfLeftLeaves(TreeNode root) {
//使用前序遍历,找出有多少个左叶子,然后加起来
//1)截止条件
if(root==null) return 0;
if(root.left==null && root.right==null) return 0;
//递归
if(root.left!=null && root.left.left==null && root.left.right==null){ //找到了左叶子
sum+=root.left.val; //(中)
}
if(root.left!=null) sumOfLeftLeaves(root.left); //(左)
if(root.right!=null) sumOfLeftLeaves(root.right); //(右)
return sum;
}
}
//分离版本
class Solution {
public int sum=0; //可以定义全局变量,但是不能随便定义静态变量,会一直保持不变的
public int sumOfLeftLeaves(TreeNode root) {
method(root);
return sum;
}
public void method(TreeNode root){
//使用前序遍历,找出有多少个左叶子,然后加起来
//1)截止条件
if(root==null || root.left==null && root.right==null) return;
//递归
if(root.left!=null && root.left.left==null && root.left.right==null){ //找到了左叶子
sum+=root.left.val; //(中)
}
if(root.left!=null) method(root.left); //(左)
if(root.right!=null) method(root.right); //(右)
}
}
- 总结
1)如果是要遍历全树,那么递归函数不能有返回值(有返回值也不能用,只能作为最后的输出),因为一旦用了,那么就会在中途某个地方停下来。
11. 找树左下角的值
- 题目

- 思路说明
1)方法一:层序遍历,对每一层的第一个数进行保留
2)方法二:递归,前序遍历:在前的操作中,保存最大深度,在出现叶子节点的时候,判断深度是否超出原来的,超出就记录一下最新的深度,并且保留左叶子节点的值。(遍历顺序,默认为第一个) - 代码展示
1)方法一:层序遍历
class Solution {
public int findBottomLeftValue(TreeNode root) {
//使用层序遍历进行寻找:输出最后一层的第一个数
ArrayDeque<TreeNode> deque=new ArrayDeque<>();
int result=0;
//截止条件
deque.offer(root);
//两层while循环
while(deque.size()>0){
List<Integer> list=new ArrayList<>();
int size=deque.size();
for(int i=0;i<size;i++){
TreeNode node=deque.poll();
if(i==0) result=node.val;
if(node.left!=null) deque.offer(node.left);
if(node.right!=null) deque.offer(node.right);
}
}
//输出(最后一层的第一个数)
return result;
}
}
2)方法二:递归遍历
class Solution {
private int maxdepth=-1;
private int depth=0;
private int result;
public int findBottomLeftValue(TreeNode root) {
method(root);
return result;
}
//递归方法(前序遍历)
public void method(TreeNode root){
//截止条件
if(root==null) return;
//(中):遇到叶子节点进行操作(必定是第一次遇到叶子节点,即层数的最左边)
//操作:更新maxdepth和result的值
if(root.left==null &&root.right==null){
if(depth>maxdepth){
maxdepth=depth;
result=root.val;
}
}
//左边
if(root.left!=null){
depth++;
method(root.left);
depth--;
}
//右边
if(root.right!=null){
depth++;
method(root.right);
depth--;
}
}
}
12. 路径总和(深度:有返回值,要对左右递归值进行判别)
- 题目描述

- 思路
1)这道题目不需要遍历全局,只需要遍历局部就可以,所以递归是带有返回值的(方便及时退出)
2)求和的过程中:遇到一个节点就减去,而不是最后拿一个集合装,简便运算
3)递归三部曲
(1):截止条件:如果遇到了叶子节点,就先判断,目前的和是否为0了
(2):不是叶子节点,就继续左右遍历,四步(1)先减去该节点的值,2)然后进行递归判断,3)如果结果为true那么就停止);4)然后跟上一个回溯(没退出)。
4)最后递归返回值为false,不满足任何一个true的条件
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
//使用迭代方法,因为不需要遍历全部,故需要带返回值
//每走一步,就减去值,如果最后某个叶子节点值为0,那么就找到了
if(root==null) return false;
return find(root,targetSum-root.val); //走了第一步
}
public boolean find(TreeNode root, int targetSum){
//截止条件(叶子节点)
if(root.left==null && root.right==null){
if(targetSum==0){
return true;
}else return false;
}
//一般情况
//左边
if(root.left!=null){
targetSum-=root.left.val;
boolean flag=find(root.left,targetSum);
if(flag==true) return true;
targetSum+=root.left.val;
}
//右边
if(root.right!=null){
targetSum-=root.right.val;
boolean flag=find(root.right,targetSum);
if(flag==true) return true;
targetSum+=root.right.val;
}
return false; //如果不满足上面为true的条件,那么就是false了
}
}
13 .路径总和ii(广度遍历)
-
题目
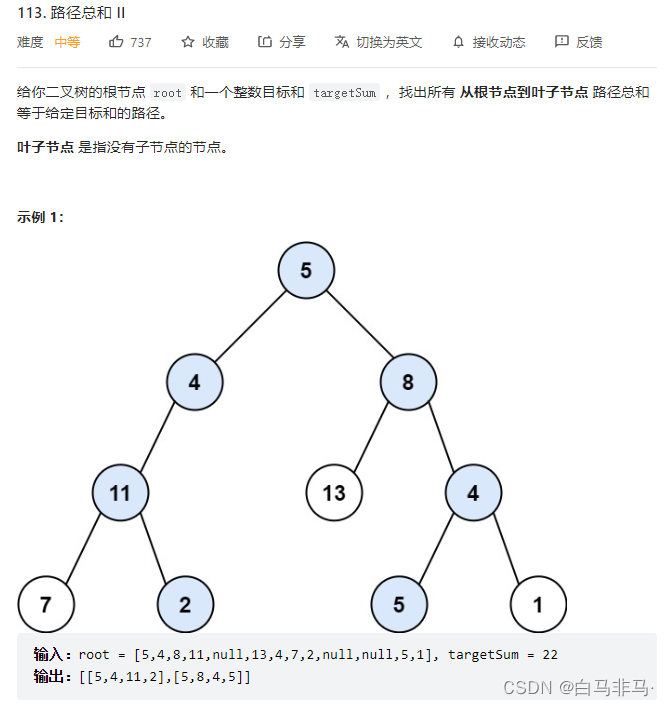
-
中心思路
1)因为需要遍历全树,故递归无返回值
2)这道题与求路径的题目非常像,知识在(中)的时候,进行一个判断,只有满足要求的才能被装进去,且是深度复制 -
代码解析
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> result=new ArrayList<>();
List<Integer> path=new ArrayList<>();
if(root==null) return result;
method(root,targetSum,result,path);
return result;
}
//前序遍历
public void method(TreeNode root, int targetSum, List<List<Integer>> result,List<Integer> path){
path.add(root.val);
//截止条件
int sum=0;
if(root.left==null && root.right==null){
for(int i:path) sum+=i;
if(sum==targetSum) result.add(new ArrayList<>(path)); //添加的时候,需要深度复制
}
//左右递归
if(root.left!=null){
method(root.left,targetSum,result,path);
path.remove(path.size()-1);
}
if(root.right!=null){
method(root.right,targetSum,result,path);
path.remove(path.size()-1);
}
}
}
14 .从中序与后序遍历序列构造二叉树(有一点绕)
- 题目说明
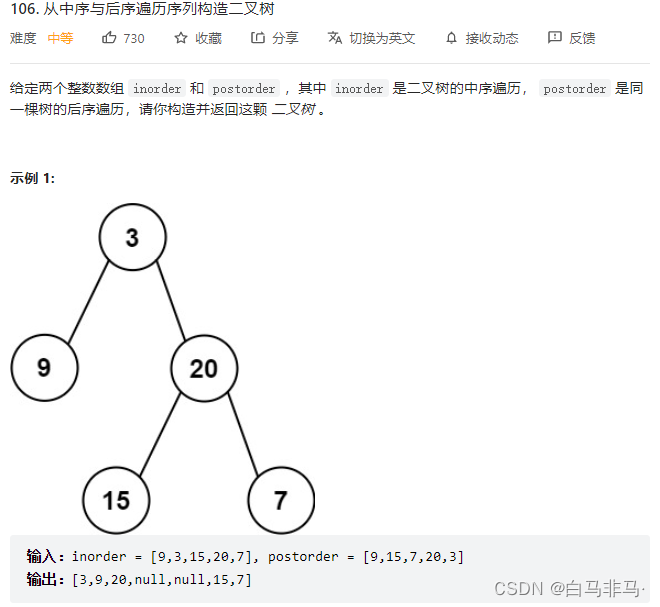
- 题目思路
1)其实就是一个递归的三部曲操作,
(1):截止条件有两个:一个是差值为0,一个是差值为1;
(2)先找到分割点的索引,然后找到分割点的值,并新建树的节点(新建树,用new TreeNode()
(3)然后递归找到左右子树,左边的两组给左边,右边的两组给右边
最后输出根节点。
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
//递归:前序遍历
return method(inorder,0,inorder.length,postorder,0,postorder.length);
}
public TreeNode method(int[]inorder, int inleft, int inright, int[]postorder, int postleft, int postright){
//1)截止条件(两种情况,一个为空,一个为单个节点)
if(inright-inleft==0) return null;
if (inright - inleft == 1) return new TreeNode(inorder[inleft]); //修改处
//2)中(找到切割点的索引值target,并且新建树节点)
int temp=postorder[postright-1]; //分割值
TreeNode root=new TreeNode(temp); //新建树节点
//在中序遍历中找到分割点的位置: 索引为:target
int target=0;
for(int i=inleft;i<inright;i++){
if(inorder[i]==temp){
target=i;
break;
}
}
//3)递归(左边和右边的节点一定要把握好)
root.left=method(inorder,inleft,target,postorder,postleft,postleft+(target-inleft)); //左开右闭
root.right=method(inorder, target+1,inright, postorder, postleft+(target-inleft),postright-1);
return root;
}
}
15 . 从前序与中序遍历序列构造二叉树(和上题一样思路)
- 题目说明
根据前序和中序遍历能够构造唯一的二叉树。思路和根据中序和后序类似,重点是左右递归参数索引的选定,比较容易弄错,可以中间输出一个日志进行说明。 - 代码说明
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
//使用递归方法
return method(preorder,0,preorder.length, inorder,0,inorder.length);
}
//方法:深搜
public TreeNode method(int[] preorder, int preleft, int preright, int[] inorder, int inleft, int inright){
//1)截止条件
if(inright-inleft==0) return null;
if(inright-inleft==1) return new TreeNode(preorder[preleft]);
//中(在前序数组中找到根节点,并且在中序遍历中找到切割位置,为后面分开左铺垫)
//新建节点,把根节点放进去
int target=preorder[preleft];
TreeNode node=new TreeNode(target);
int targetsize=0; //中序遍历位置
for(int i=inleft;i<inright;i++){
if(inorder[i]==target){
targetsize=i;
break;
}
}
//System.out.println("targetsize="+targetsize);
//找到中序遍历和前序遍历分割后的索引值(包前不包后) 这个次序容易搞混,可以输出日志验证一下
//System.out.println((preleft+1)+","+(targetsize-inleft+preleft+1)+","+inleft+","+targetsize);
//System.out.println(targetsize-inleft+(preleft+1)+","+preright+","+targetsize+","+inright);
node.left=method(preorder,preleft+1,targetsize-inleft+(preleft+1), inorder,inleft,targetsize);
node.right=method(preorder,targetsize-inleft+(preleft+1),preright, inorder,targetsize+1,inright);
return node;
}
}
