文章目录
一、电容元件
电容器:
两个导体极板,中间由绝缘材料隔开,构成一个电容器。
在外电源作用下,正、负电极上分别带上等量异号电荷。
撤去电源,电极上的电荷仍可长久地聚集下去,是一种储存电能的元件。
电容元件:
储存电能的两端元件。
任何时刻其储存的电荷q与其两端的电压u能用q-u平面上的一条曲线来描述。

线性时不变电容元件
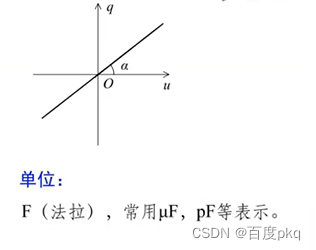
任何时刻,电容元件极板上的电荷q与电压u成正比。
q-u特性曲线是过原点的直线。

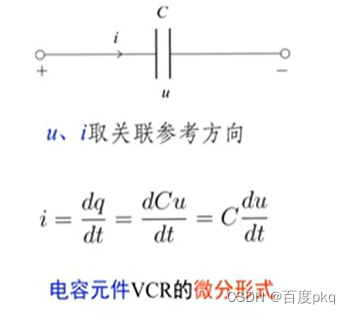
电容的电压-电流关系
某一时刻i的大小取决于u的变化率。而与该时刻电压u的大小无关。
电容是动态元件。
当u为常数(直流)时,i=0。电容相当于开路,电容有隔断直流作用。
实际电路中通过电容的i为有限值,则u必定是时间的连续函数。
某一时刻的ut)值与-o到该时刻的所有电流值有关。
电容元件有记忆电流的作用。称电容元件为记忆元件。
②研究某一to以后的u(t),需知道to时刻开始的电流i和to时刻电压u(to)。


电容的储能和功率
功率:
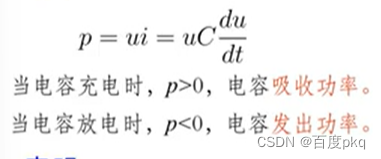
电容能在一段时间内吸收能量,转化为电场能量储存起来。
在另一段时间内将能量释放给电路。
因此电容元件是储能元件。
储能:

二、电感元件
电感线圈
把金属导线绕在一骨架上可构成一实际电感线圈。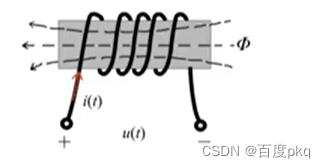
当电流通过线圈时,将产生磁通。
是一种抵抗电流变化、储存磁能的元件。
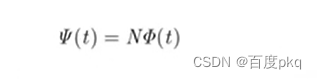
电感元件定义
存储磁能的两端元件

线性时不变电感元件

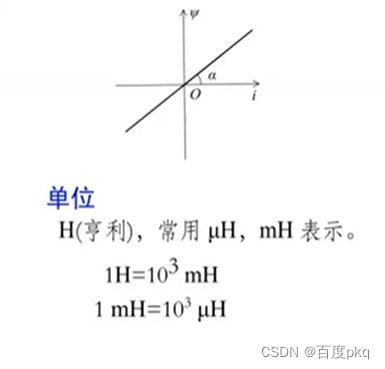
电感的电流电压关系
某一时刻u的大小取决于i的变化率。而与该时刻电流i的大小无关。
电感是动态元件。
当i为常数(直流)时,u=0。电感相当于短路。
实际电路中电感的电压u为有限值。则i必定是时间的连续函数。

某一时刻的i(t)与-∞ 到该时刻的所有电压值有关。
电感元件有记忆电压的作用。称电感元件为记忆元件。
研究某一to以后的i(t),需知道t时刻开始的电压u(t)和to时刻电流 i(to)。


电感的储能和功率
功率:
电感能在一段时间内吸收能量并转化为磁场能量储存起来。
在另一段时间内将能量释放给电路。
因此电感元件是无源元件、储能元件。
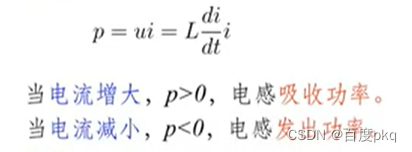
储能:

三、动态电路的方程
动态电路
含有动态元件电容和电感的电路称为动态电路。
特点:
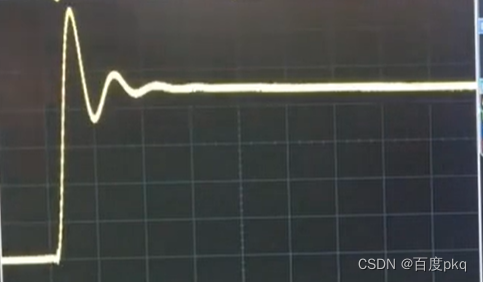
当动态电路状态发生改变时,经过一个变化过程
才能达到一个新的稳定状态。变化的过程称为过度过程。
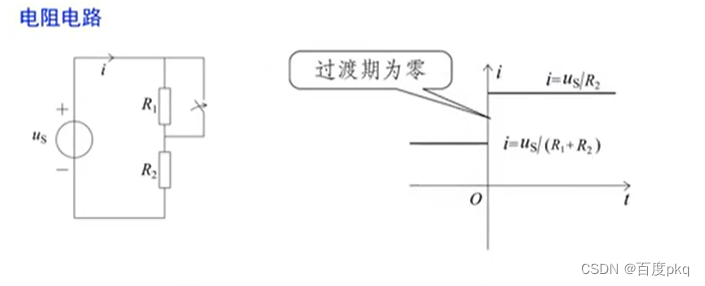
电容电路
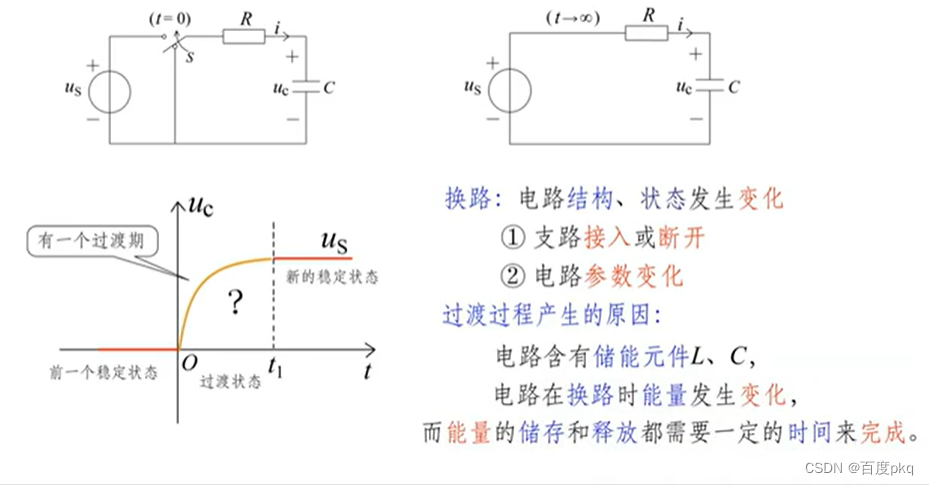
动态电路的方程
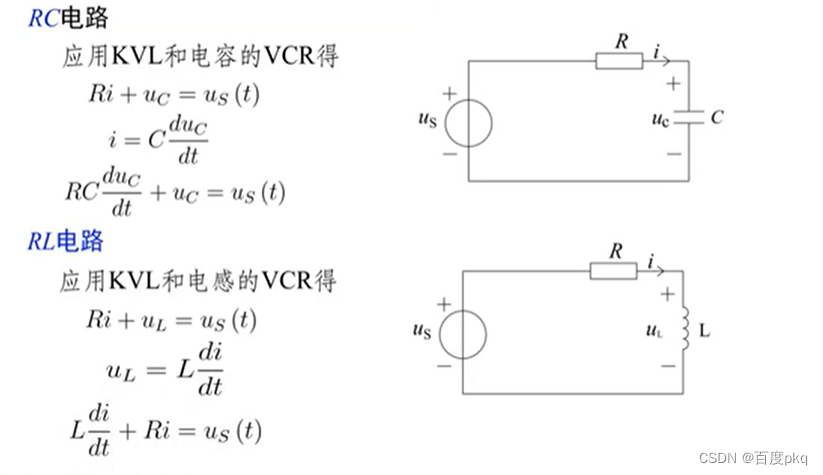
含有一个动态元件的线性电路,其方程为一阶线性常微分方程,称为一阶电路。
含有两个动态元件的线性电路,其方程为二阶线性常微分方程,称为二阶电路。
结论:
①描述动态电路的电路方程为微分方程。
②动态电路方程的阶数通常等于电路中动态元件的个数。
动态电路的分析方法:
①根据KVL、KCL和VCR建立微分方程。
②求解微分方程。(采用时域分析法中的经典法。)
四、动态电路的初始条件
初始条件:
对动态电路来说,初始条件就是电容的初始电压或电感的初始电流。
为什么要确定动态电路的初始条件?
动态电路的初始条件对于电路随时间发展的行为影响也很大,求解动态电路的微分方程也必须知道电路变量的初始值。
0+和0_是什么意思?
0±0_为一个无穷小的数


如何确定动态电路的初始条件
先确定初始条件对应的时间点是哪个。
动态电路的初始时间点是0+,开关动作后的电路动态行为是需要关注的,对电容来说,充电放电是需要一段时间的,电量q的积累或者释放都需要一个过程。
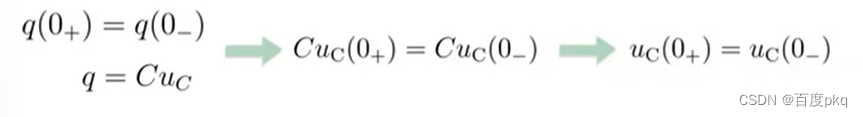
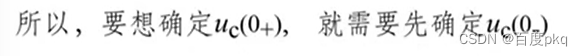

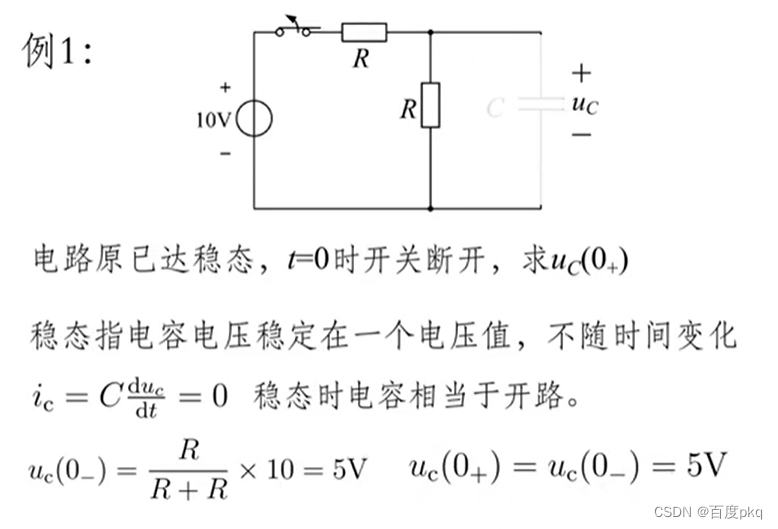
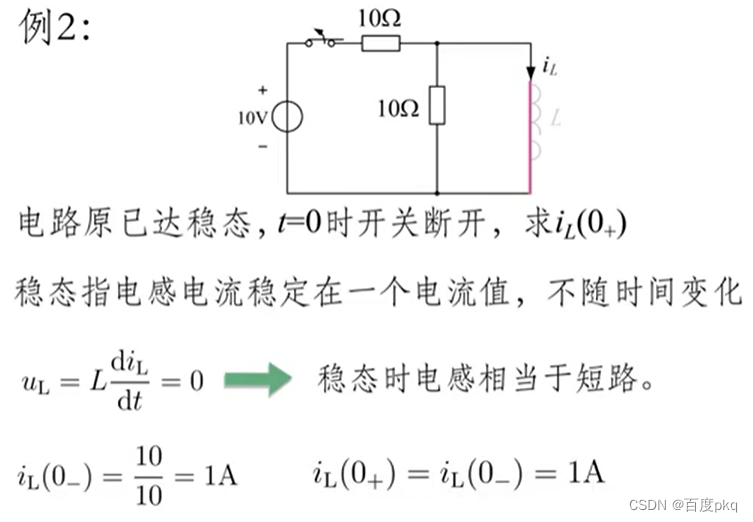
五、一阶电路的零输入响应

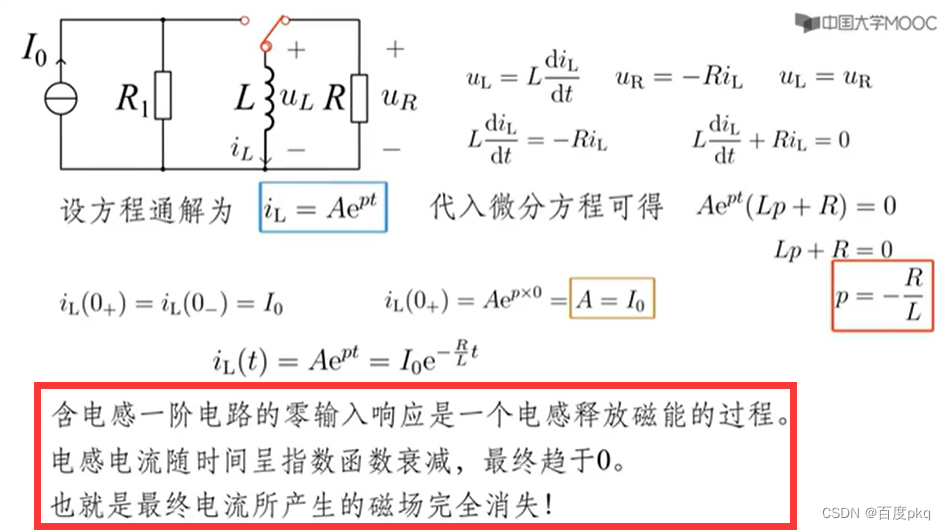
一阶电路的零 状态 响应
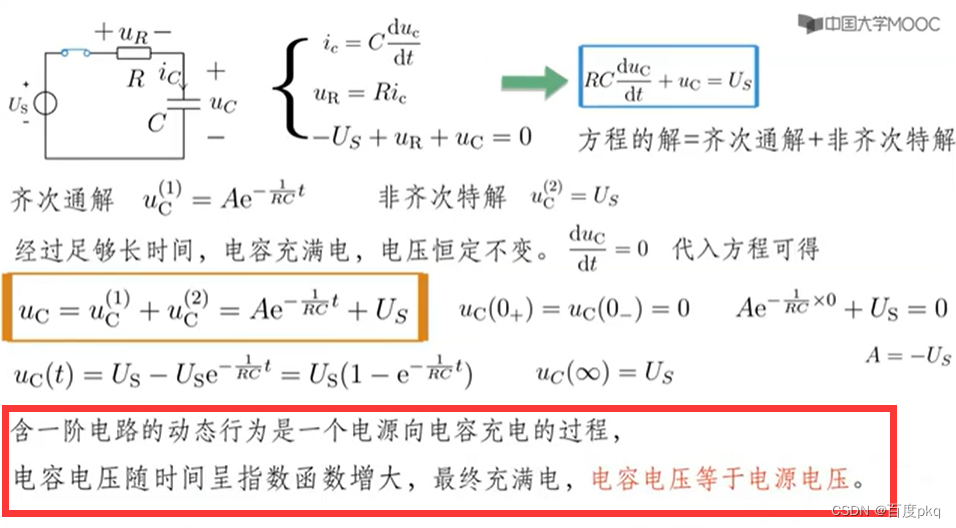
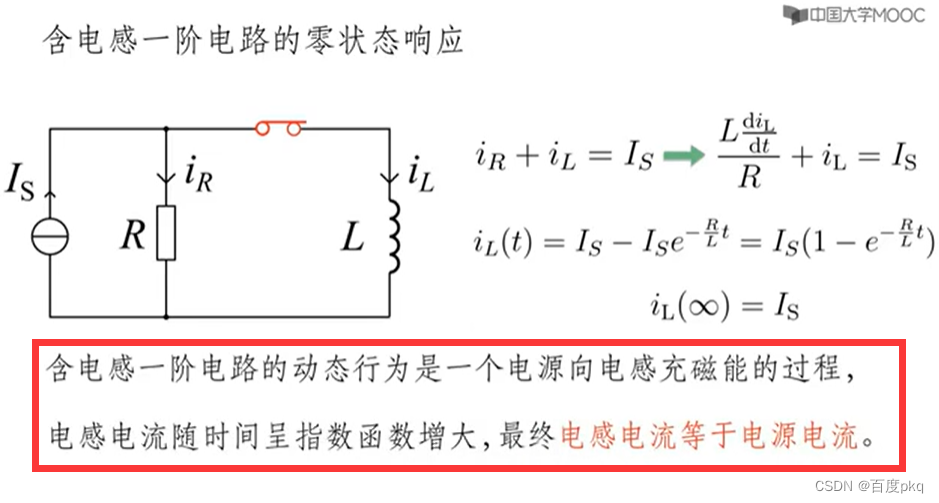
一阶电路的全响应
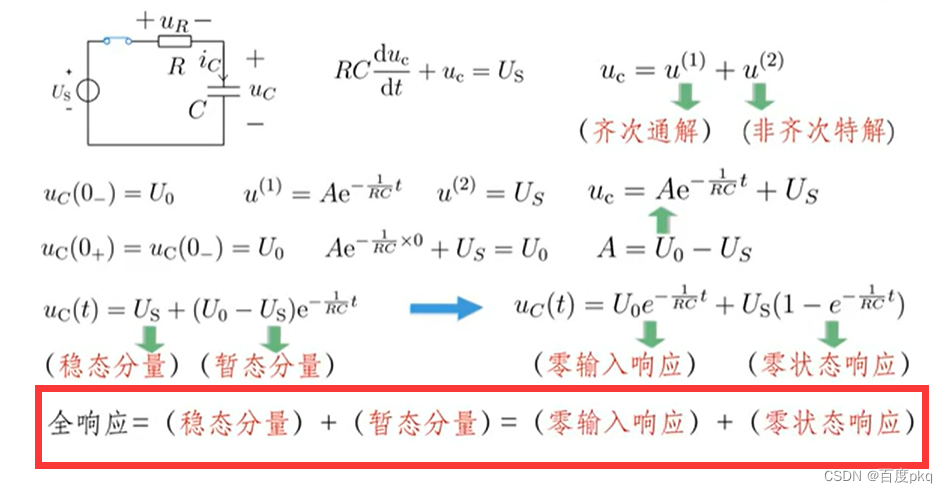
六、一阶电路分析三要素法
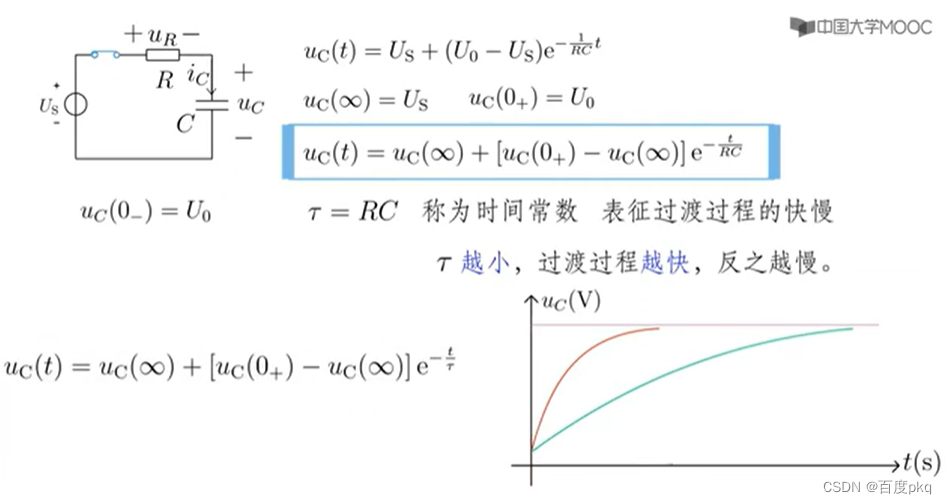
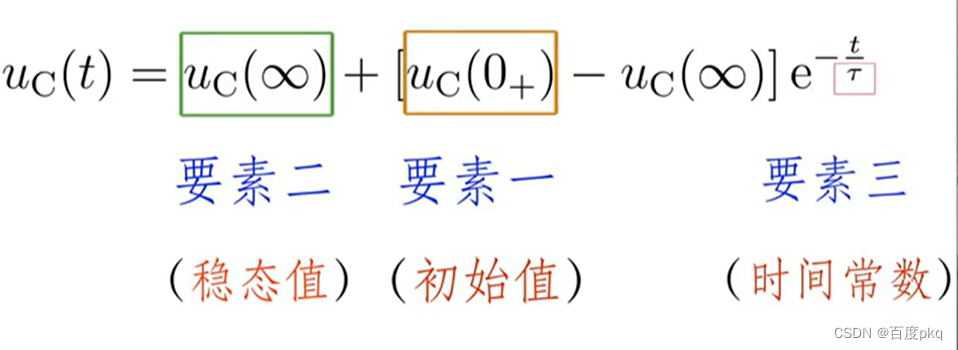
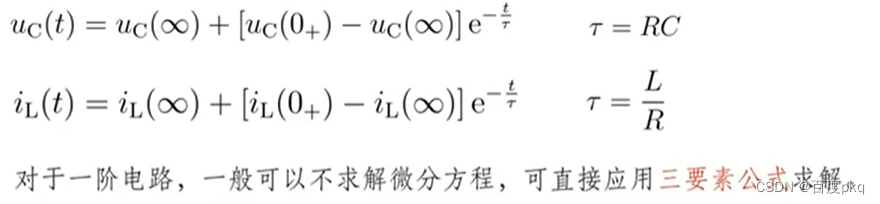

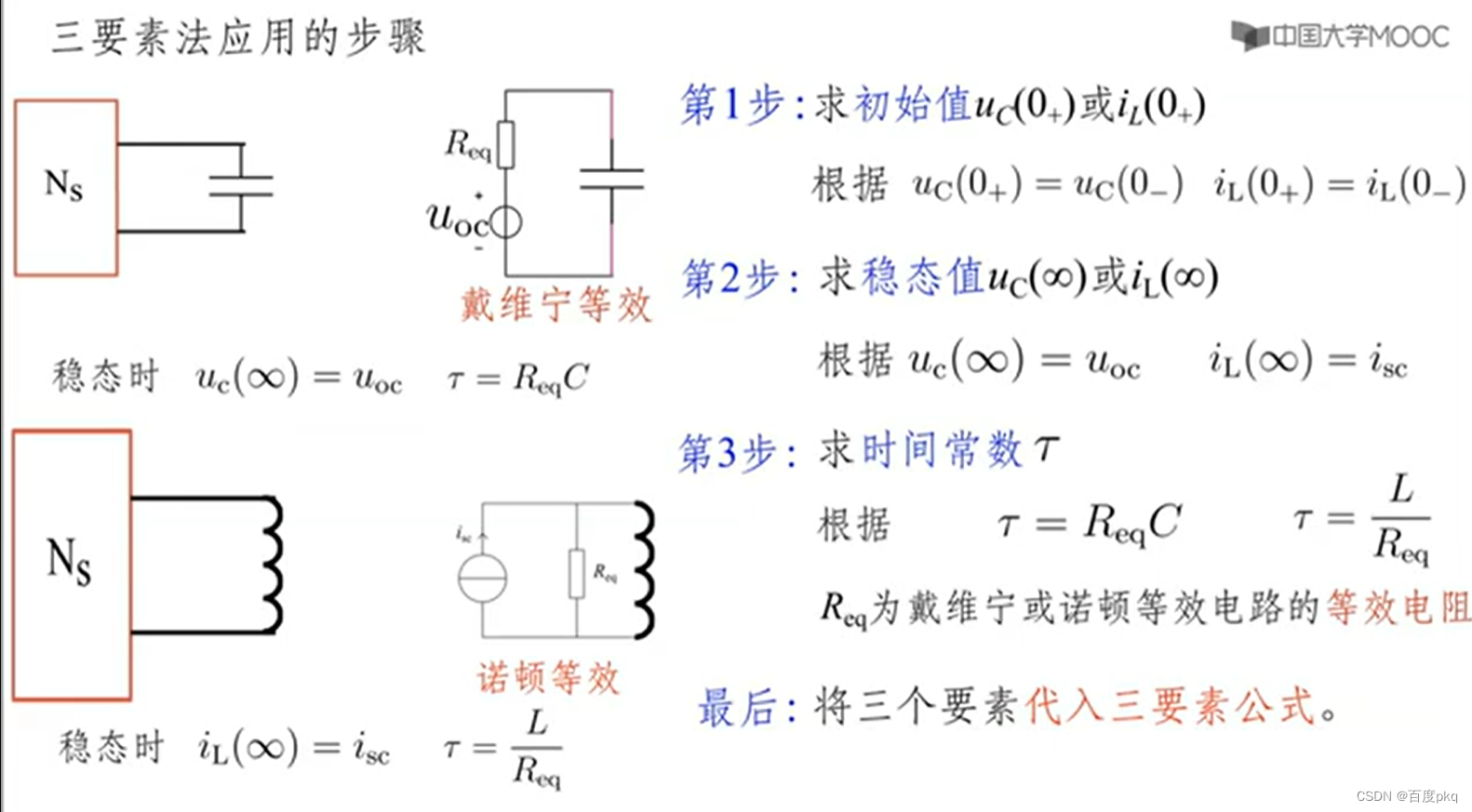
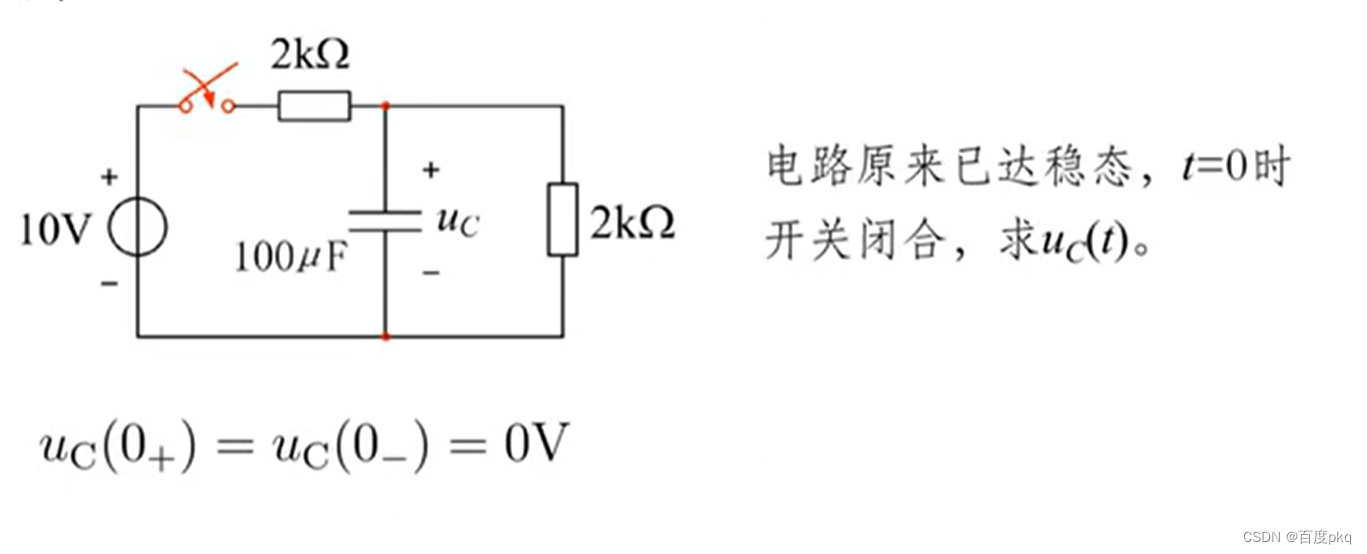
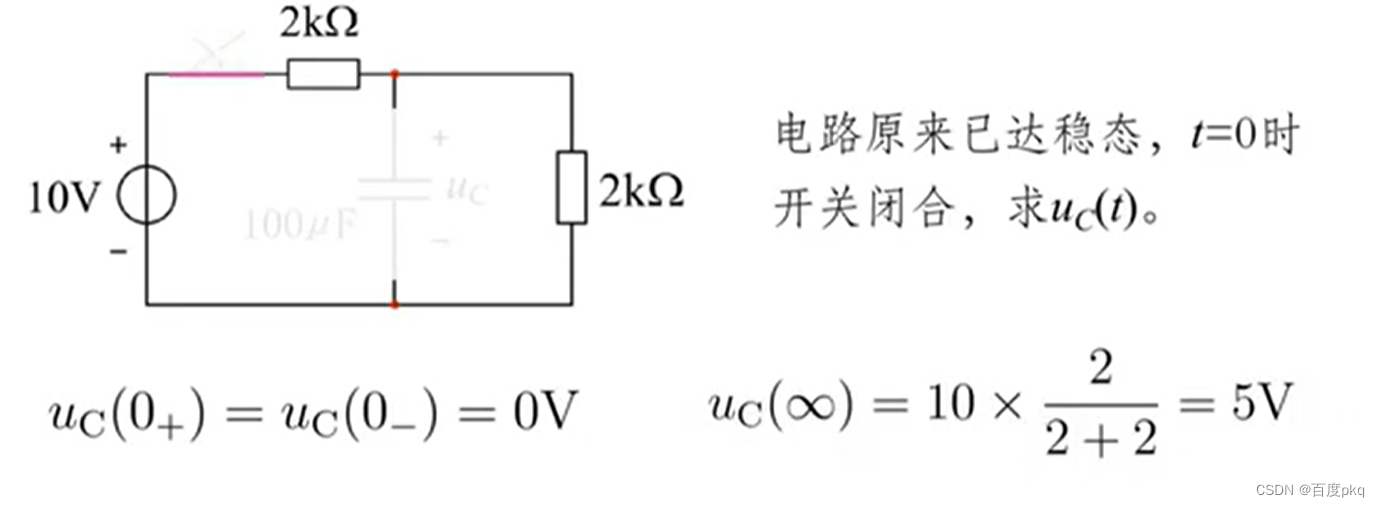
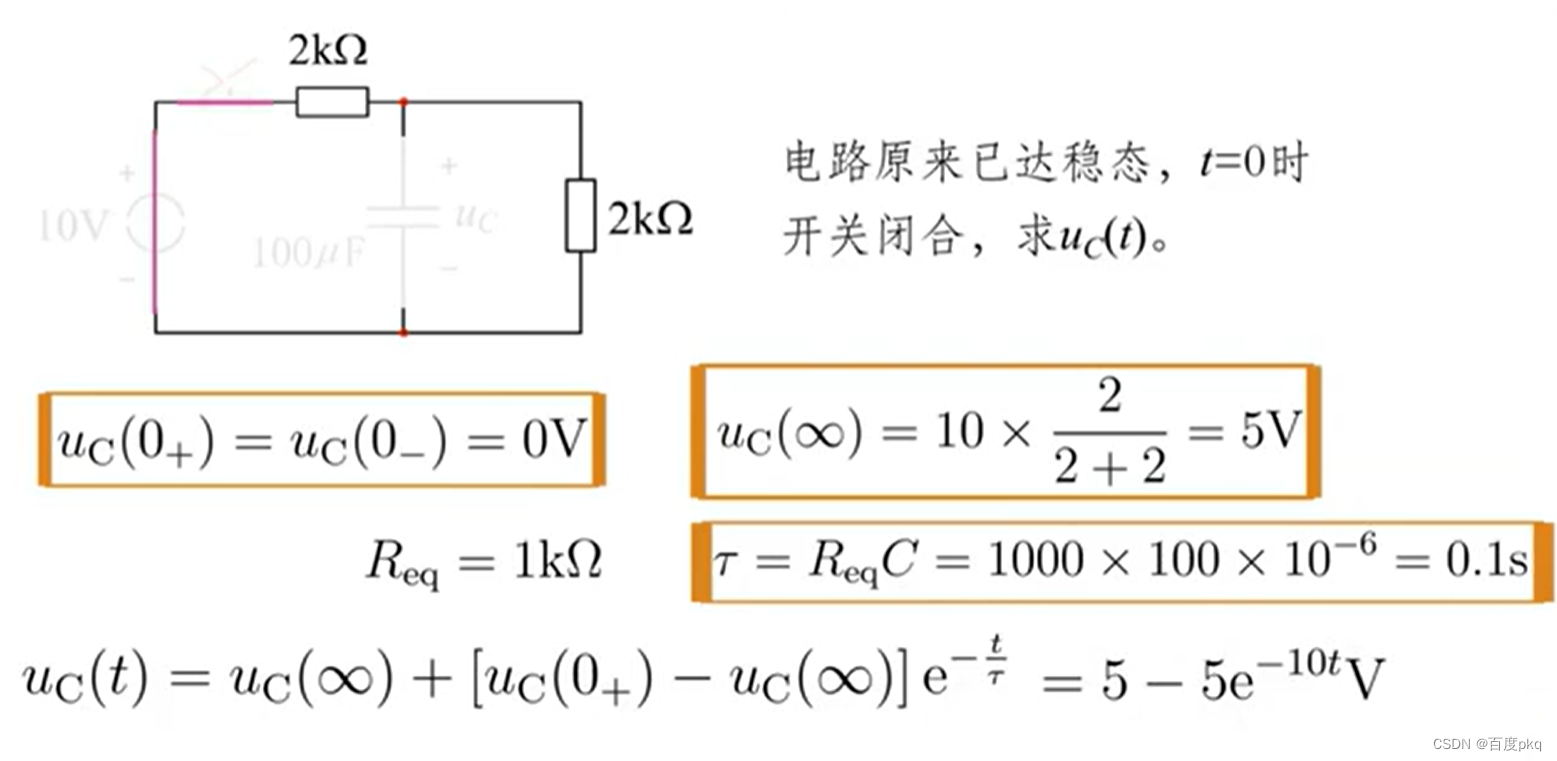
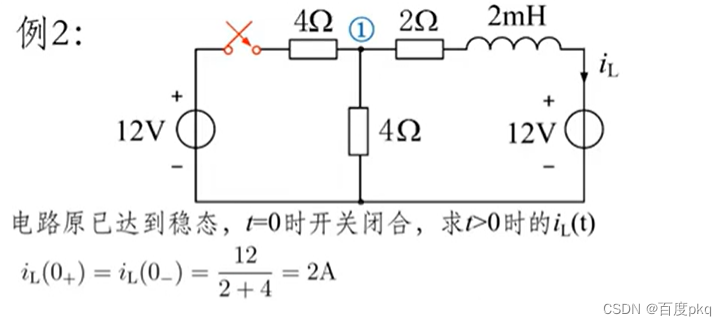
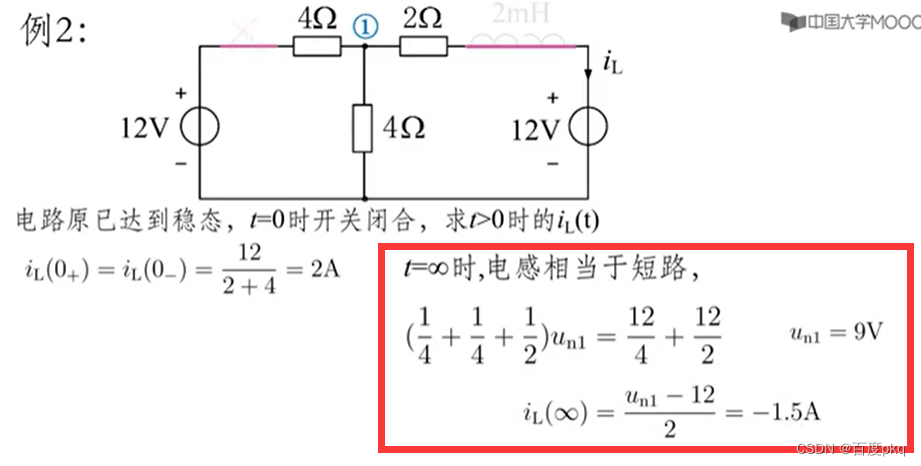

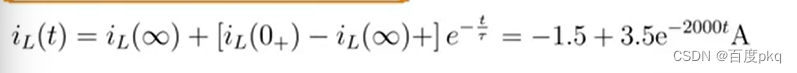
七、二阶电路
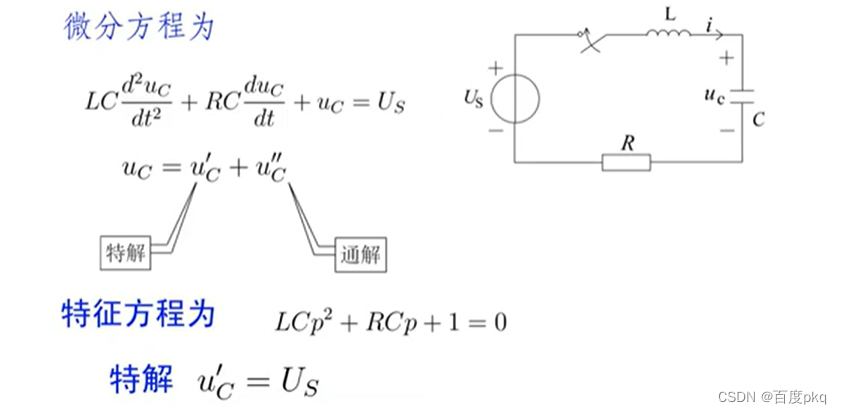
二阶电路的方程
含有二个动态元件的线性电路,称为二阶电路。
其电路方程为二阶线性常微分方程。
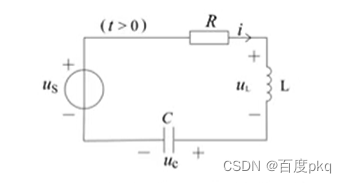
RLC电路,应用KVL和VCR得:
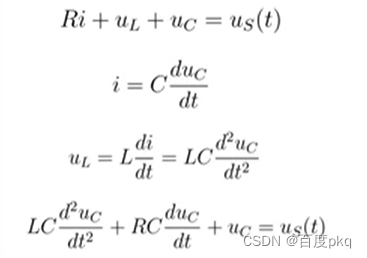

二阶电路的零输入响应
是一个齐次方程。由于输入激励项为0,所以uc以及其他电路变量称为零输入响应。
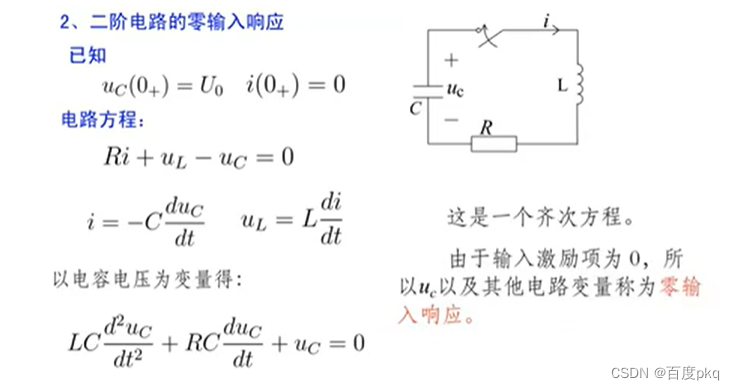

零输入响应的三种情况


二阶电路零状态响应和全响应

过阻尼

欠阻尼