树的子结构
题目链接:https://leetcode-cn.com/problems/shu-de-zi-jie-gou-lcof/
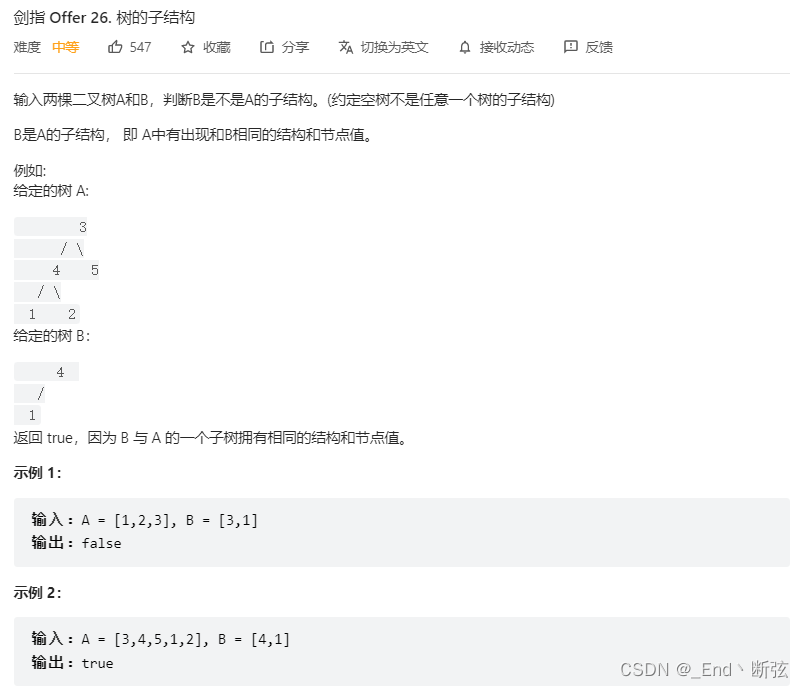
跟给定一个字符串,再给个子串判断是不是上面的子串的问题是一样的解决方法
- 先遍历树A中的每个结点,设为na
- 判断树A中已na为根节点的子树是否包含树B
基本步骤:
-
将判断是否为子结构函数设为isPart:
终止条件:
1.当结点B为空,说明树B匹配完成,返回true
2.当结点A为空,说明已经超过树A叶子结点,返回false
3.当结点A和B的值不相等,返回false -
返回值:
1.判断 A和 B的左子节点是否相等,即 isPart(A->left, B->left) ;
2.判断 A和 B的右子节点是否相等,即 isPart(A->right, B->right) ;
isSubStructure(TreeNode* A, TreeNode* B) :
- 特殊处理:题目给定空树返回false,需要处理一下
- 返回值: 若树 BB 是树 AA 的子结构,则必满足以下三种情况之一,因此用或 || 连接;
1.以 节点 A 为根节点的子树 包含树 B ,对应 isPart(A, B);
2.树 B 是 树 A 左子树 的子结构,对应 isSubStructure(A->left, B);
3.树 B 是 树 A 右子树 的子结构,对应 isSubStructure(A->right, B);
代码如下:
class Solution {
public:
bool isSubStructure(TreeNode* A, TreeNode* B) {
if(!A || !B) return false;
if(isPart(A,B)) return true;
return isSubStructure(A->left,B) || isSubStructure(A->right,B);
}
bool isPart(TreeNode* p1,TreeNode* p2)
{
if(!p2) return true;
if(!p1 || p1->val != p2->val) return false;
return isPart(p1->left,p2->left) && isPart(p1->right,p2->right);
}
};
复杂度:
- 时间复杂度:O(MN),M,N分别是树A,树B的结点数量
- 空间复杂度:O(M)当树 A 和树 B 都退化为链表时,递归调用深度最大。当 M≤N 时,遍历树 A 与递归判断的总递归深度为 M ;当 M>N 时,最差情况为遍历至树 A 叶子节点,此时总递归深度为 M。
二叉树的镜像
题目链接:https://leetcode-cn.com/problems/er-cha-shu-de-jing-xiang-lcof/
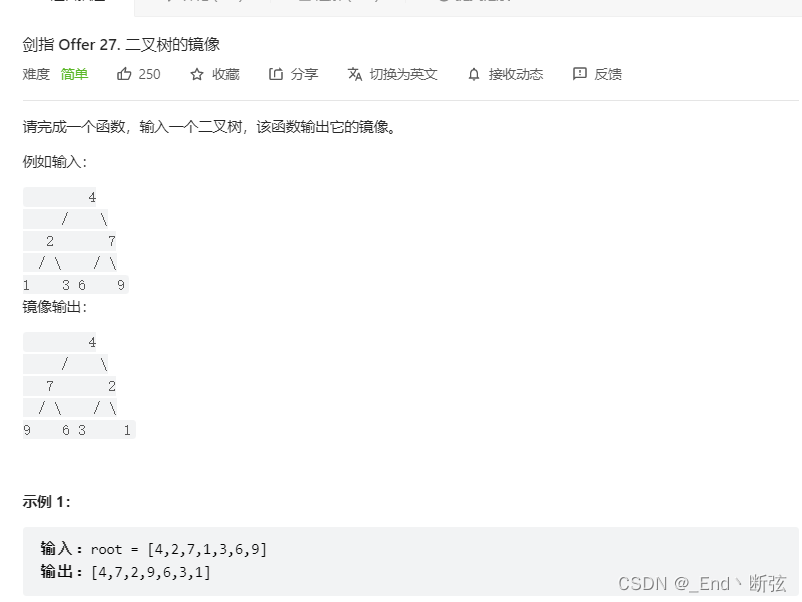
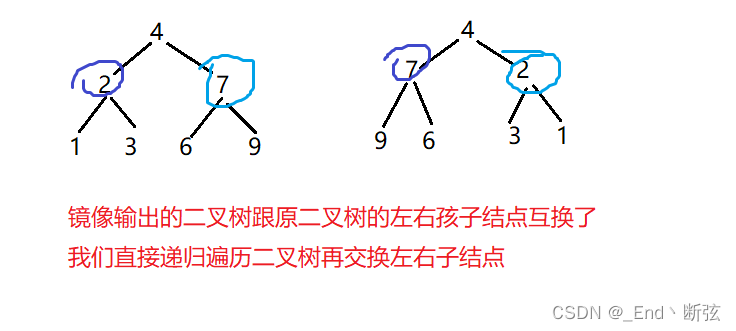
代码如下:
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
if(!root) return nullptr;
mirrorTree(root->left);
mirrorTree(root->right);
swap(root->left,root->right);
return root;
}
};
复杂度:
- 时间复杂度:O(N)
- 空间复杂度:O(N),极端情况树退化成链状
对称的二叉树
题目链接:https://leetcode-cn.com/problems/dui-cheng-de-er-cha-shu-lcof/
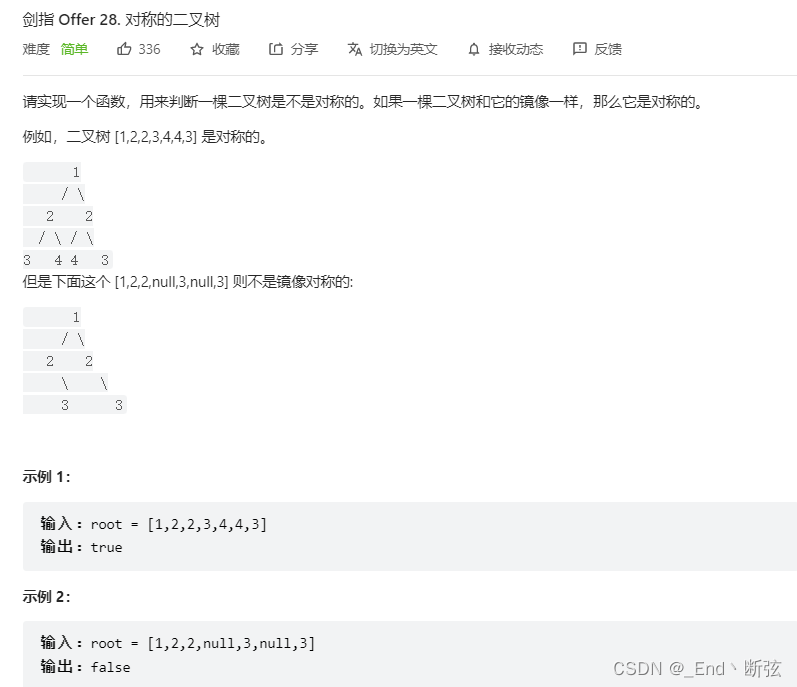
思路:
步骤:
递归终止条件:
1.当 L 和 R 同时越过叶节点: 此树从顶至底的节点都对称,因此返回 true
2.当 L或 R中只有一个越过叶节点: 此树不对称,因此返回 false
3.当节点 L值 不等于节点R值,返回false
递归工作:
判断L->left是否和R->right相等;
判断L->right是否和R->left相等;
代码如下:
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(!root) //树为空返回true
return true;
return dfs(root->left,root->right);
}
bool dfs(TreeNode* r1,TreeNode* r2){
if(!r1 && !r2) //2个结点走完
return true;
if(!r1 || !r2)//有1个没走完
return false;
if(r1->val != r2->val)//2个的值不相等
return false;
return dfs(r1->left,r2->right) && dfs(r1->right,r2->left);
}
};
复杂度:
- 时间复杂度:O(N)
- 空间复杂度:O(N)
二叉树中和为某一值的路径
题目链接:https://leetcode-cn.com/problems/er-cha-shu-zhong-he-wei-mou-yi-zhi-de-lu-jing-lcof/
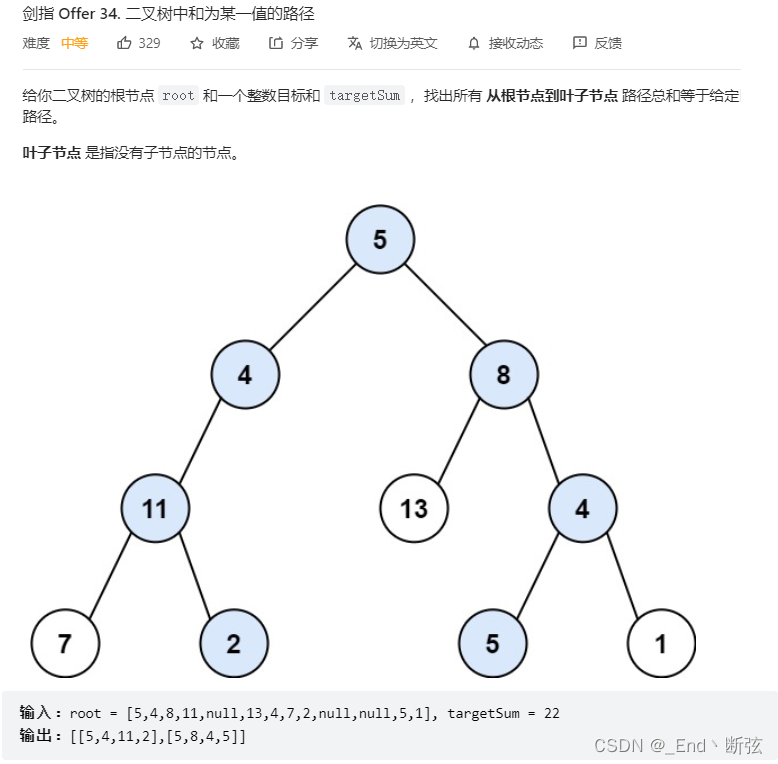
解题思路:使用回溯,包括
先序遍历+路径记录2个部分
- 先序遍历:按照根、左、右遍历树的所有节点
- 路径记录:在先序遍历中,记录从根节点到当前节点的路径。当路径为 ① 根节点到叶节点形成的路径 且 ② 各节点值的和等于目标值 sum 时,将此路径加入结果列表。
本题我们可以直接用减法,这样可以少传参数
- 递归参数:当前结点root,目标值
- 终止条件:若结点为空,直接返回
- 递归工作:
1.路径更新:将当前的结点的val加入路径
2.目标值更新:目标值减到0、
3.路径记录: 当 ① root 为叶节点 且 ② 路径和等于目标值 ,则将此路径 path 加入 res
4.先序遍历: 递归左 / 右子节点
5. 路径恢复: 向上回溯前,需要将当前节点从路径 path 中删除,即执行 path.pop()
动图演示:

代码如下:
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
vector<vector<int>> pathSum(TreeNode* root, int target) {
dfs(root,target);
return ans;
}
void dfs(TreeNode* root,int sum)
{
if(!root) return;
path.push_back(root->val);
sum -= root->val;
if(!root->left && !root->right && !sum ) ans.push_back(path);
dfs(root->left,sum);
dfs(root->right,sum);
path.pop_back();
}
};
复杂度:
- 时间复杂度:O(N)
- 空间复杂度:O(N)

