机动目标跟踪——交互式多模型算法IMM
原创不易,路过的各位大佬请点个赞
WX: ZB823618313
机动目标跟踪——交互式多模型算法IMM
1.交互式多模型算法流程
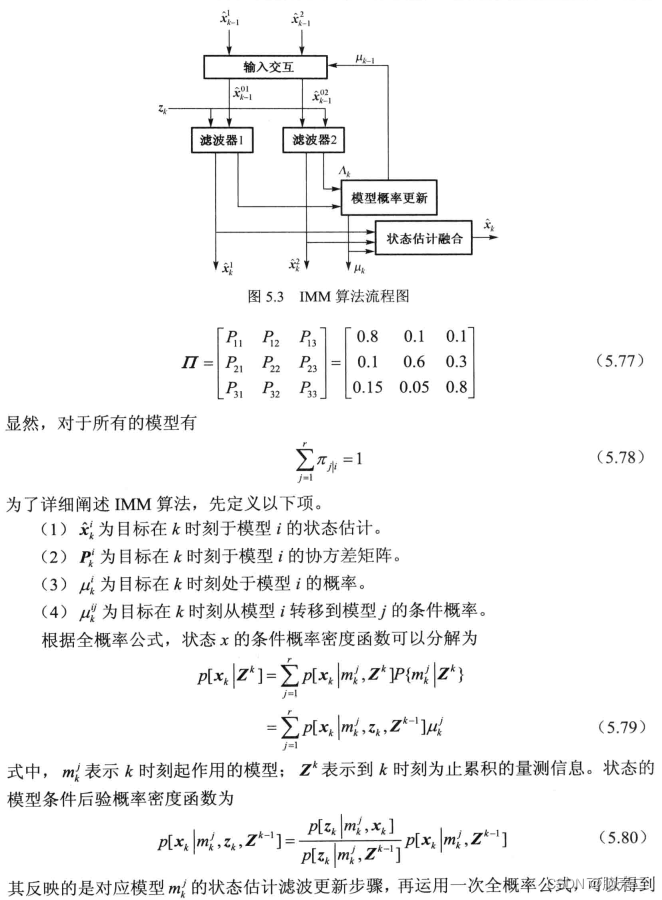
核心思想: IMM算法的基本思想是用多个不同的运动模型匹配机动目标的不同运动模式,不同模型间的转移概率是–个马尔可夫矩阵,目标的状态估计和模型概率的更新使用卡尔曼滤波。其算法流程图如图5.3所示。

2. 交互式多模型:具体推导




3. IMM+KF目标跟踪
WX: ZB823618313
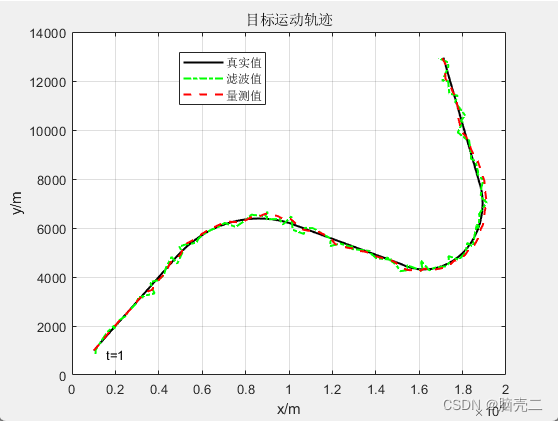
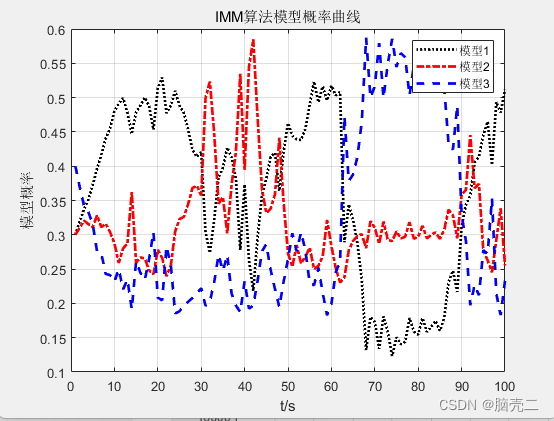
部分代码
clear all;
clc;
echo off;
close all;
%===============================
%建立模型
%===============================
% 仿真参数
simTime=100; %仿真迭代次数
T=1; %采样时间
w2=3*2*pi/360; %模型2转弯率3度
w3=-3*2*pi/360; %模型3转弯率-3度
H=[1,0,0,0;0,0,1,0]; %模型量测矩阵
G=[T^2/2,0;T,0;0,T^2/2;0,T]; %模型过程噪声加权矩阵
r=20000; %20 2000
R=[r,0;0,r]; %模型量测噪声协方差矩阵
Q=[20,0;0,20]; %模型过程噪声协方差矩阵
F1=[1,T,0,0;0,1,0,0;0,0,1,T;0,0,0,1]; %模型1状态转移矩阵
F2=[1,sin(w2*T)/w2,0,(cos(w2*T)-1)/w2;
0,cos(w2*T),0,sin(w2*T);
0,(1-cos(w2*T))/w2,1,sin(w2*T)/w2;
0,-sin(w2*T),0,cos(w2*T)]; %模型2状态转移矩阵 左转弯
F3=[1,sin(w3*T)/w3,0,(cos(w3*T)-1)/w3;
0,cos(w3*T),0,sin(w3*T);
0,(1-cos(w3*T))/w3,1,sin(w3*T)/w3;
0,-sin(w3*T),0,cos(w3*T)]; %模型3状态转移矩阵 右转弯
w4=3*2*pi/360; %模型2转弯率3度
w5=-6*2*pi/360; %模型3转弯率-3度
F4=[1,sin(w4*T)/w4,0,(cos(w4*T)-1)/w4;
0,cos(w4*T),0,sin(w4*T);
0,(1-cos(w4*T))/w4,1,sin(w4*T)/w4;
0,-sin(w4*T),0,cos(w4*T)]; %模型2状态转移矩阵
F5=[1,sin(w5*T)/w5,0,(cos(w5*T)-1)/w5;
0,cos(w5*T),0,sin(w5*T);
0,(1-cos(w5*T))/w5,1,sin(w5*T)/w5;
0,-sin(w5*T),0,cos(w5*T)]; %模型3状态转移矩阵
x0=[1000,200,1000,200]'; % 初始状态
% 产生量测数据
%[z,z_true]=targets();
randn('state',sum(100*clock)); % Shuffle the pack!
x = zeros(4,simTime);
z = zeros(2,simTime); %含噪声量测数据
z_true = zeros(2,simTime); %真值数据
measureNoise = zeros(2,simTime);
measureNoise = sqrt(R)*randn(2,simTime); %产生量测噪声
x(:,1)=x0;
z(:,1)=H*x(:,1)+measureNoise(:,1);
z_true(:,1)=H*x(:,1);
for a=2:simTime
if (a>=20)&&(a<=40)
x(:,a)=F4*x(:,a-1); %20--40s左转
elseif (a>=60)&&(a<=80)
x(:,a)=F5*x(:,a-1); %60--80s右转
else
x(:,a)=F1*x(:,a-1); %匀速直线运动
end;
z(:,a)=H*x(:,a)+measureNoise(:,a);
z_true(:,a)=H*x(:,a);
end;
4. IMM+EKF目标跟踪
WX: ZB823618313
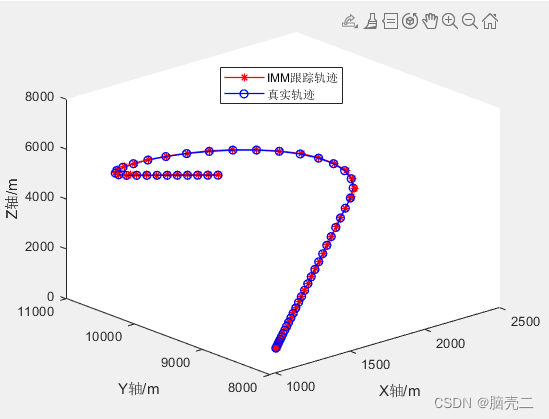
原创不易,路过的各位大佬请点个赞
