给你一个下标从 0?开始大小为 m x n?的二维整数数组?grid?,它表示一个网格图。每个格子为下面 3 个值之一:
0 表示草地。
1 表示着火的格子。
2?表示一座墙,你跟火都不能通过这个格子。
一开始你在最左上角的格子?(0, 0)?,你想要到达最右下角的安全屋格子?(m - 1, n - 1)?。每一分钟,你可以移动到?相邻?的草地格子。每次你移动 之后?,着火的格子会扩散到所有不是墙的 相邻?格子。
请你返回你在初始位置可以停留的 最多 分钟数,且停留完这段时间后你还能安全到达安全屋。如果无法实现,请你返回 -1?。如果不管你在初始位置停留多久,你 总是?能到达安全屋,请你返回?109?。
注意,如果你到达安全屋后,火马上到了安全屋,这视为你能够安全到达安全屋。
如果两个格子有共同边,那么它们为 相邻?格子。
示例 1:
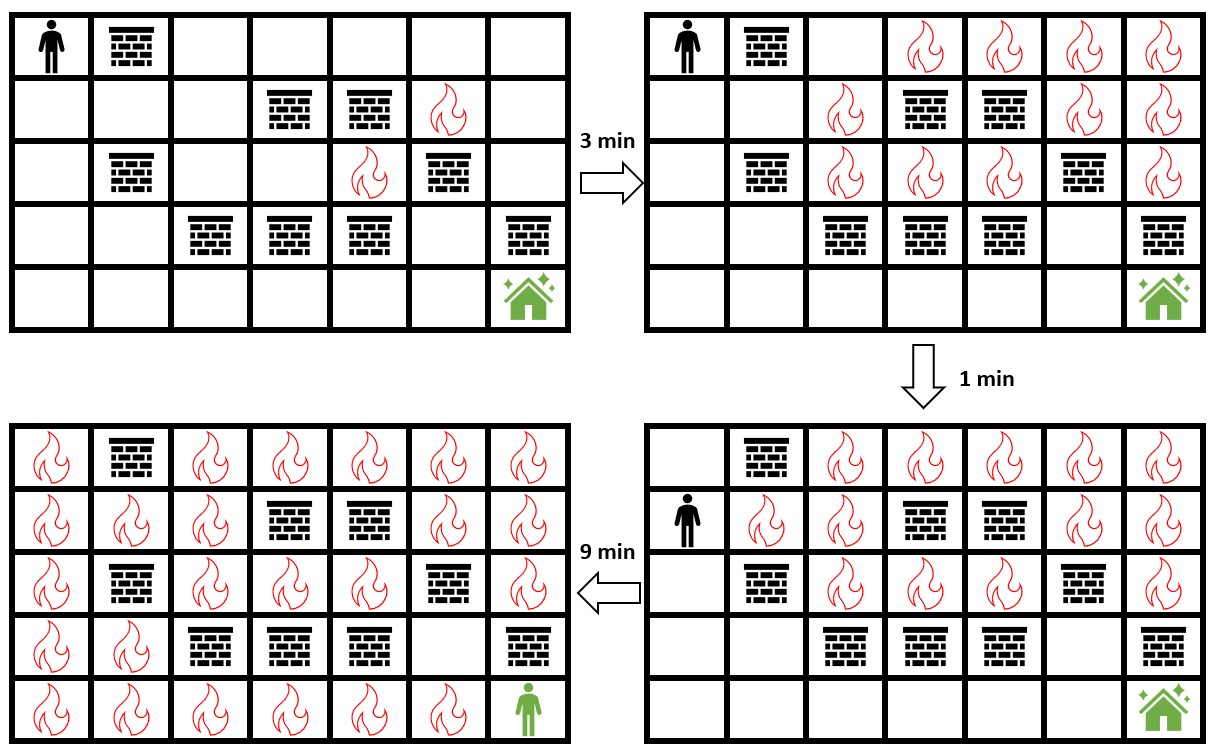
输入:grid = [[0,2,0,0,0,0,0],[0,0,0,2,2,1,0],[0,2,0,0,1,2,0],[0,0,2,2,2,0,2],[0,0,0,0,0,0,0]]
输出:3
解释:上图展示了你在初始位置停留 3 分钟后的情形。
你仍然可以安全到达安全屋。
停留超过 3 分钟会让你无法安全到达安全屋。
示例 2:
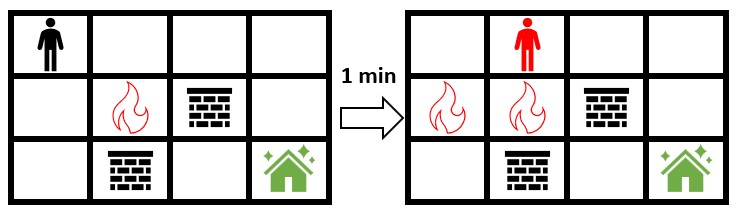
输入:grid = [[0,0,0,0],[0,1,2,0],[0,2,0,0]]
输出:-1
解释:上图展示了你马上开始朝安全屋移动的情形。
火会蔓延到你可以移动的所有格子,所以无法安全到达安全屋。
所以返回 -1 。
示例 3:

输入:grid = [[0,0,0],[2,2,0],[1,2,0]]
输出:1000000000
解释:上图展示了初始网格图。
注意,由于火被墙围了起来,所以无论如何你都能安全到达安全屋。
所以返回 109 。
?
提示:
m == grid.length
n == grid[i].length
2 <= m, n <= 300
4 <= m * n <= 2 * 10^4
grid[i][j]?是?0?,1?或者?2?。
grid[0][0] == grid[m - 1][n - 1] == 0
PS:通过的人数较少,以为是个难题,做起来发现其实只是一个常规的广搜问题。
思路:由于存在火苗蔓延的问题,我们可以先预处理出火苗能够蔓延到的点,只需保存最快蔓延到达相应位置的时间即可,简单的广搜即可处理。对于火苗蔓延不到的地方,可以设置为一个比较大的值便于区分。之后从玩家的位置再进行一次广搜,并记录到达相应位置时与火苗达到该位置的时间差,对于任意一条路径,需要记录的是时间差的最小值【这点应该不难理解,如果你中途遇到火不就没啦】。最终答案就是所有路径里求得的最小时间差的最大值。
注意一个坑点:火苗和你同时达到安全屋视为没烧到,因此安全屋的位置要特殊处理!
class Solution {
public:
struct Node {
int x, y, step, mnTime;
Node(int x, int y, int step, int mnTime) {
this->x = x;
this->y = y;
this->step = step;
this->mnTime = mnTime;
}
};
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, -1, 1};
int maximumMinutes(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<vector<int>> lastTime(m, vector<int>(n)), used(m, vector<int>(n));
queue<Node> q;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j) {
lastTime[i][j] = 100000000;
if (grid[i][j] == 1) {
lastTime[i][j] = 0;
q.push(Node(i, j, 0, 0));
}
}
while (!q.empty()) {
Node now = q.front(); q.pop();
for (int i = 0; i < 4; ++i) {
int x = now.x + dx[i];
int y = now.y + dy[i];
if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y]== 2 || lastTime[x][y] <= now.step + 1)
continue;
lastTime[x][y] = now.step + 1;
q.push(Node(x, y, now.step + 1, 0));
}
}
int ans = -1;
q.push(Node(0, 0, 0, lastTime[0][0]));
while (!q.empty()) {
Node now = q.front(); q.pop();
if (now.x == m - 1 && now.y == n - 1) {
ans = max(ans, now.mnTime);
continue;
}
for (int i = 0; i < 4; ++i) {
int x = now.x + dx[i];
int y = now.y + dy[i];
if (x == m - 1 && y == n - 1 && lastTime[x][y] >= now.step + 1) {
used[x][y] = 1;
q.push(Node(x, y, now.step + 1, min(now.mnTime, lastTime[x][y] - now.step - 1)));
continue;
}
if (x < 0 || x >= m || y < 0 || y >= n || grid[x][y]== 2 || lastTime[x][y] <= now.step + 1 || used[x][y])
continue;
used[x][y] = 1;
q.push(Node(x, y, now.step + 1, min(now.mnTime, lastTime[x][y] - now.step - 2)));
}
}
if (ans > m * n)
return 1000000000;
return ans;
}
};