人工智能—— Chapter02 Search
问题导向:
- 我们想采取一些行动来改变世界的状态(但由行为引起的变化完全是可以预料到的)
- 我们试着采取一系列的行动引导我们达到目标状态(可能是最小化行动的次数,也可能是最小化行动的总成本)
- 不需要在现实生活中执行行动的同时找到最小解决方案(让所有事都在意料之中)
重要知识点:
Q1:A search problem consists of?
- A state space S (状态空间——所有节点)
- An initial state s0(初始状态)
- Actions A(s) in each state(每个状态下的行动)
- Transition model Result(s,a)(移动模型——移动方式)
- A goal test G(s)(目标状态)
- Action cost c(s,a,s’)(行动损失)
+1 per step; -10 food; -500 win; +500 die; -200 eat ghost
EXAMPLE——Traveling in Romania
分析Search问题:
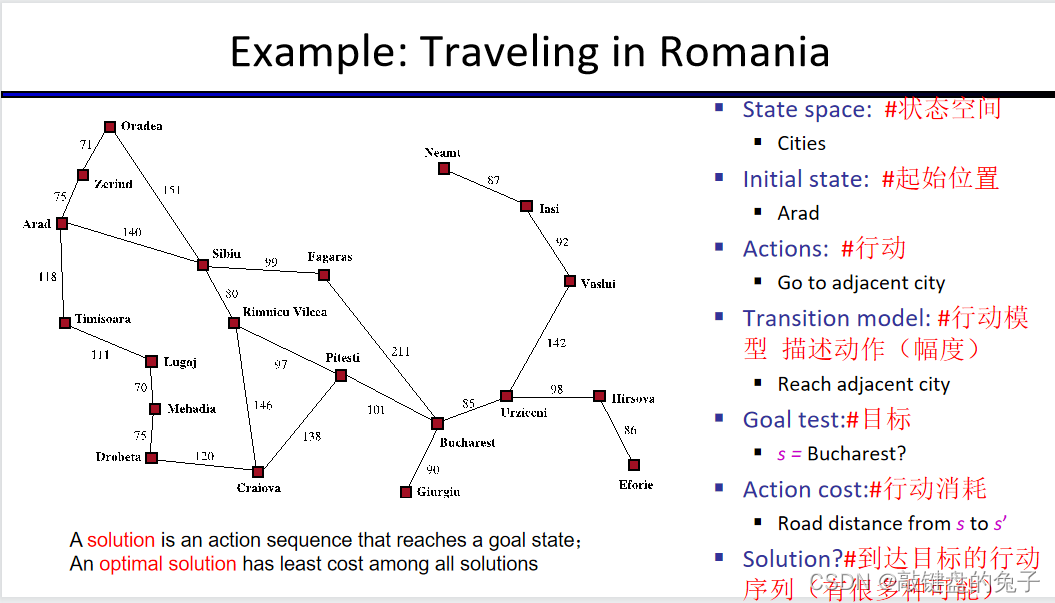
Uninformed Search Methods——盲目搜索
Q2:Uninformed Search Methods and specify the difference?
- Depth-First Search
- Breadth-First Search
- Uniform-Cost Search
DFS expands a deepest node first.
BFS expands a shallowest node first.
UCS expands the lowest g(n) or cost from root to n.
Q3:What is the difference between state space graphs and search trees?
- Each node in the search tree is an entire PATH in the state space graph.(搜索树中的每个节点都是状态空间图中的一个完整的PATH)
- In a state space graph, each state occurs only once.(在状态空间图中,每个状态只出现一次)
- In a state space graph,the goal test is a set of goal nodes (maybe only one).(在状态空间图中,目标测试是一组目标节点(可能只有一个)
- We construct the tree on demand – and we construct as little as possible.(我们按需构造树,并且尽可能少地构造)
Informed Search——启发式搜索
搜索过程中利用与问题有关的经验信息,引入估计函数(evaluation function)来估计节点位于解路径上的“希望”,函数值越小“希望”越大。
启发函数:
用来描述经验信息;描述从当前这个节点到目标节点的最优路径代价的估计。一般用h(n)来表示。
- A算法:
f(x) = g(x) +h(x)
g(x):从起始状态到当前状态x的代价
h(x):从当前状态x到目标状态的估计代价(启发函数) 是代入实际问题的真实代价,是实际值
- A*算法——最有效的直接搜索算法:
f *(n) =g *(n) + h * (n)
f*(n):从初始状态经由状态n到目标状态的最小代价估计
g*(x):从起始状态到当前状态x的代价
h*(n) :从状态n到目标状态的路径的最小估计代价 是对剩余距离的估算值,是一种理想值
A*算法是由A算法约束得到的,在A算法的基础上添加一定的条件:g(x)必须大于0,其次h(x)的要求是必须是不大于x到目标的实际代价。
h*(n)是理论上的最短路径,h(n)是实际A*算法拟合的函数,是实际值
0 <= h(n) <= h*(n)
当实际值h(n) 无限逼近理论值h * (n) ,取到h * (n)的下界,即 h(n) = h * (n)时,此时搜索效率最高,取到最优解
- 表示有修饰,最优路径的修饰,则是理论值
例如:对于几何路网来说,可以取两节点间曼哈顿距离做为距离估计。
【注意】:A算法并不能保证一定找到最优解,然后A*算法可以保证一定找到最优解。
【实际应用举例】:
八数码问题
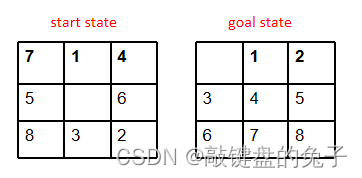
情形1、If heuristic is the number of tiles misplaced
如果启发式是放错瓷砖的数量(表示所有瓷砖都可以任意放置)
h(start)= 7
【快速解题方法】:
解析:在所有的8块方块中,1的位置前后不变,所以只有7块元素位置不同,所以答案为7
思路总结:在所有瓷砖中,放错的瓷砖(起始状态与终状态摆放不一致的瓷砖)的个数,即为最终答案==》有几个方块目标状态不同,结果就是几个
情形2、 If heuristic is that any tile could slide any direction at any time
如果启发式是任何贴图可以在任何时间向任何方向滑动
h(start)=16
【快速解题方法】:
解析:h(start)=3+0+2+3+2+2+2+2=16
思路总结:初始状态中每块瓷砖到达目标位置需移动的步数,累加,sum即为最终答案
Q4、What is an admissible heuristic h(n)?
什么是可接受的启发式搜索?
A heuridtic h is admissible if : 0<=h(n)<=h*(n),where h*(n) is the true cost to a nearest goal.
Q5、A * tree search is optimal when heuristic is admissible and A * graph search is optimal when heuristic is consistent.
