一、周期序列的离散傅里叶级数(DFS)
对于上面这段话要补充说明的是:
①DFS的全称为Discrete Fourier Series
②连续时间信号下的
Ω
=
2
π
T
\Omega =\frac{2\pi }{T}
Ω=T2π?为基波角频率,由于T的单位为秒(s),所以其单位为rad/s。离散序列下的
Ω
=
2
π
N
\Omega =\frac{2\pi }{N}
Ω=N2π?为数字角频率,由于N是没有单位的,所以其单位为rad,即把
2
π
2\pi
2π分成N份。这一点要特别注意,即要注意区分角频率和数字角频率的不同。
③要注意小写字母n的意义和小写字母k的意义。小写字母n是对基波角频率或基波数字角频率的倍增,而k是从连续时间信号的t转变而来的。

从以上图片我们知道了为什么n的取值我们可以限定到n=0,1,2 …,N-1

注意上面这幅图片中离散傅里叶系数的表达式
F
N
(
n
)
F_{N}(n)
FN?(n)是怎样的。要明白其中N、n、k、Ω的含义。
要注意:傅里叶系数和傅里叶级数是不一样的,在工程的频域分析中,我们常常用到的是实际上是傅里叶系数。

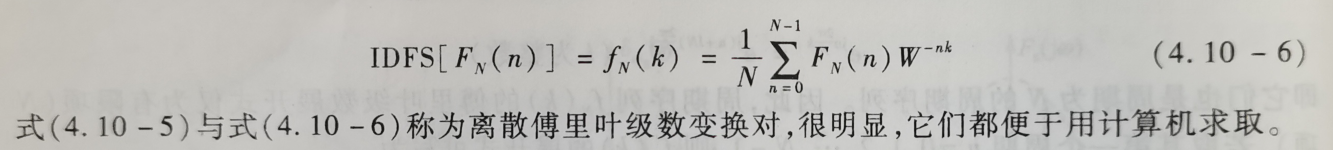
W代表的表达式要清楚,在工程中我们经常遇到这样的表示方法。
二、离散傅里叶变换(DFT)
以上内容为周期序列的离散傅里叶级数的相关内容,接下来我们切入到本文的正题,即序列的离散傅里叶变换(DFT)是怎么回事。

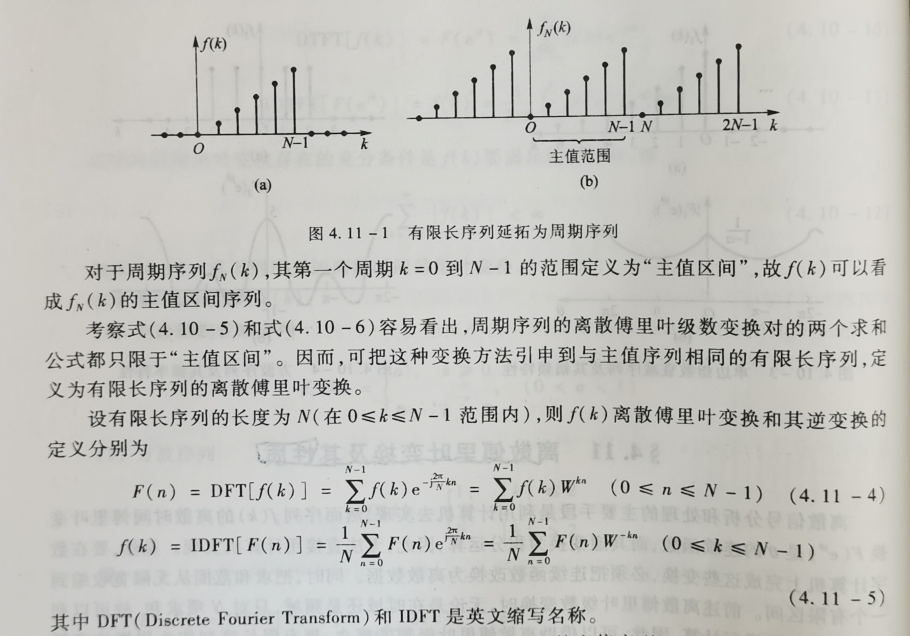
看了以上两张照片,我们便知道了DFT的来源。原来,DFT是把我们的有限长的离散序列延拓为周期离散序列后,对这个延拓的周期离散序列求离散傅里叶系数的变换。我们平时在做DFT时脑子里要知道DFT求得的傅里叶系数是哪个序列的系数。
三、利用MATLAB的函数FFT()求序列的DFT

上面的图就说明了FFT的来历。MATLAB提供了函数FFT()用于计算序列的DFT。
下面是使用函数FFT()的示例,在该示例中我们利用函数FFT()来计算服从正态分布的序列的频谱。
代码如下:
N = 2000;
norm_sequence_01 = normrnd(0,1,1,N);
DFT_01 = fft(norm_sequence_01);
DFT_01_abs = abs(DFT_01);
digital_frequency = linspace(0,(2*pi/N)*(N-1),N);
plot(digital_frequency,DFT_01_abs);
运行结果如下图所示:
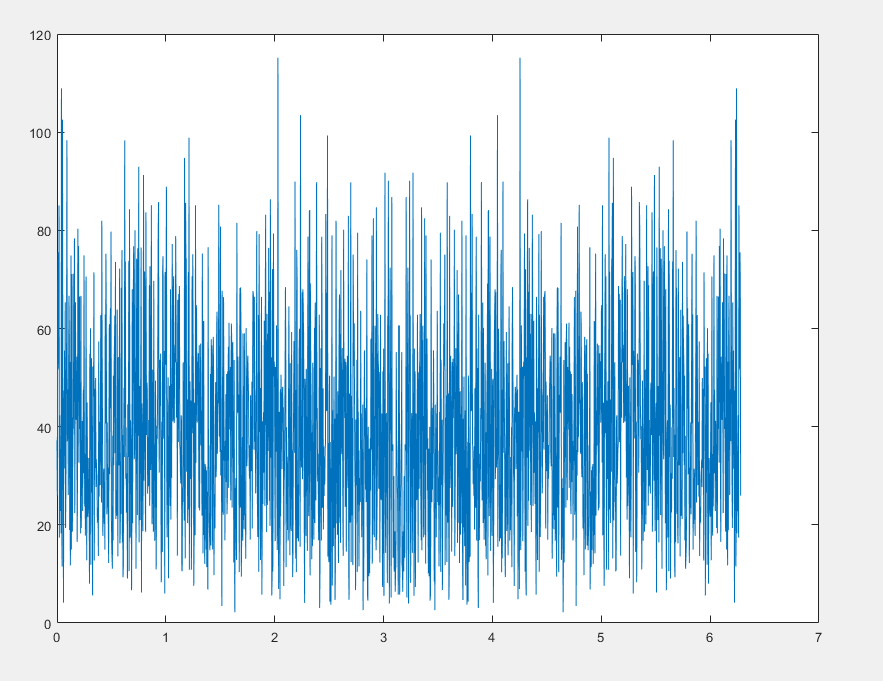
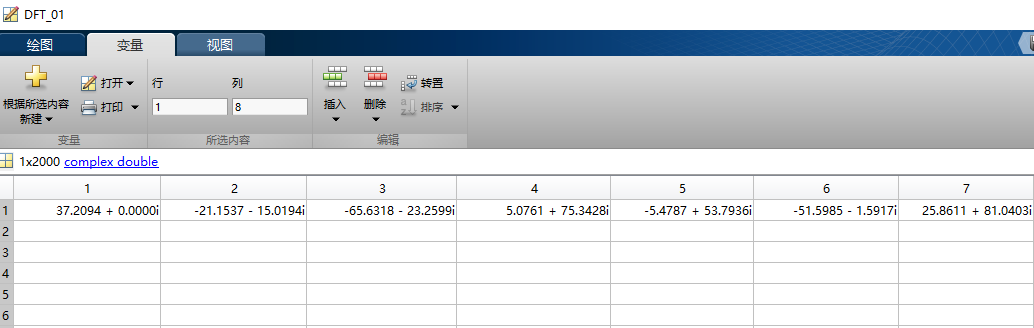
从该运算结果我们可以看出以下3点:
① 序列的DFT是关于π对称的;
② 服从正态分布的序列的频谱在整个数字频谱上几乎是均匀的,这就导致我们没法使用滤波器将其完全滤除。
③ 序列的DFT是复数。
