
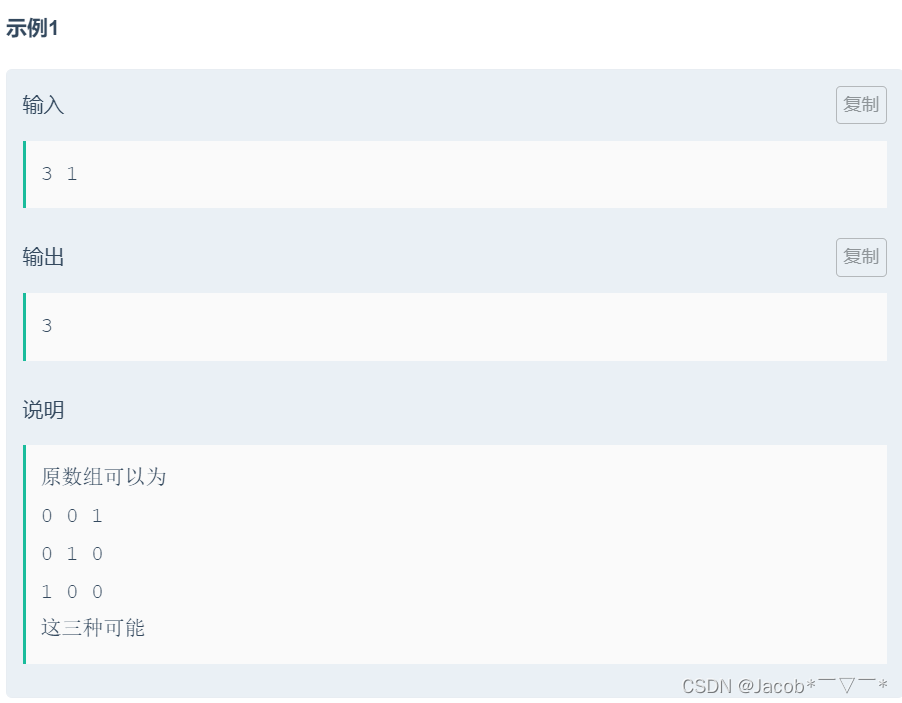
题意:
任意一个长度为 n 的 a 数组,已知其总和 a[+] 为 m,问:有多少种不同的 a 数组,使得其 总异或和 a[⊕] 达到最大值?
思路:
观察题目给定数据范围,可知肯定又是找规律了。
当直接想发现不出什么规律时,我们可以尝试的写写暴力求解的程序,我们以 n = 3 为例(当 n = 1 or 2 时直接在草稿纸上计算),m 自定义输入,计算出可能的种类数 cnt,以及所有可能结果中的 a 数组的最大异或和 mx。
下面的程序建议copy到本地编译器上运行(注意本程序仅代表 n = 3、m 为任意值 的情况)
#include<bits/stdc++.h>
using namespace std;
string trans(int x) //返回一个整数的二进制表示的 string
{
string s;
for(int i=0; i<32; ++i)
{
int t = x >> i & 1;
s += to_string(t);
}
while(s.back()=='0' && s.size()!=1) s.pop_back();
reverse(s.begin(), s.end());
return s;
}
int main()
{
int m;
while(printf("输入 a 数组总和 m:\n\n"), cin>>m)
{
cout<<"a 数组总和 m 的二进制表示:"<<trans(m)<<endl;
puts("");
int mx = -1;
int cnt = 0;
printf("当 a 数组异或和达到最大时,a1、a2、a3具体有以下情况:\n\n");
for(int a1=0; a1<=m; ++a1)
{
for(int a2=0; a2<=m; ++a2)
{
for(int a3=0; a3<=m; ++a3)
{
if(a1+a2+a3==m)
{
mx = max(mx, a1 ^ a2 ^ a3);
if((a1 ^ a2 ^ a3)==m)
{
++cnt, cout<<"a 数组:"<<a1<<' '<<a2<<' '<<a3<<endl;
cout<<"a1 二进制表示 "<<trans(a1)<<'\n';
cout<<"a2 二进制表示 "<<trans(a2)<<'\n';
cout<<"a3 二进制表示 "<<trans(a3)<<'\n';
puts("");
}
}
}
}
}
cout<<"最大异或和 mx "<<mx<<endl;
cout<<"异或和最大时,a 数组可能的种类数:cnt "<<cnt<<endl;
puts("");
}
return 0;
}
通过多次输入 m,并运行程序输出结果,我们可以初步得出结论:
对于一个包含 n 个元素的 a 数组,当其总和为 m 时,其最大异或和即为 m。
这个结论的得出不一定要根据上面的暴力程序才能得到,通过在草稿纸上写几组样例也可以得出。(对于 多个数 的 异或运算,即 按位 进行“不进位加法”,根据这一原则在草稿纸上演算即可)
由上面得出的结论,对于一个长为 n,总和为 m 的 a 数组,其 异或和取最大值 时我们可以轻易 构造出一个方案,
即:首元素为 m,其余 n - 1 个元素均为 0,
进而根据异或运算的性质,我们发现对于 首元素中 1 所在位置,我们 任意将这些位置上的 1 随机 “覆盖” 到其它元素(0) 的对应位置,即可 得到其他的方案,
由于对于首元素中的每个 1,都可以 选择 n 个位置进行覆盖,因此当 异或和取最大时,根据简单 乘法原理,得出:
总方案数 ans 等于 a 数组长度 n ^ 首元素中 1 的个数 count
最后,注意本题要开 long long,且观察到 n 给出的范围是大于 模数 mod 的范围的,因此输入的时候就要先对 n 取模。
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 1e9+7;
inline int lowbit(int x) { return x & (-x); }
signed main()
{
int n, m; cin>>n>>m;
n = n % mod;//输入 n 之后要记得马上取模
//求 m 的二进制表示中 1 的个数
int cnt = 0;
while(m) ++cnt, m -= lowbit(m);
//乘法原理求方案数
int ans = 1;
while(cnt--) ans = ans * n % mod;
cout<<ans<<'\n';
return 0;
}
