【树形动态规划】968. 监控二叉树——思路分析
968. 监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
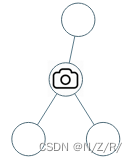
输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
思路分析【树形动态规划】
本题以二叉树为背景,不难想到用递归的方式求解。本题的难度在于如何从左、右子树的状态,推导出父节点的状态。
为了表述方便,我们约定:如果某棵树的所有节点都被监控,则称该树被「覆盖」。
对于每个节点分成三种状态:
0状态:代表该节点无覆盖的情况
1状态:代表该节点放置一个摄像头的情况
2状态:代表该节点不放置摄像头,但被覆盖的情况
那么我们很明显需要对树进行后序遍历,在遍历的同时记录放置的摄像头的数量。
1、当该节点的左孩子或右孩子处于0状态,则该节点一定要放置摄像头
2、当该节点的左右孩子都处于2状态,为了尽可能少使用摄像头,需要将摄像头尽量放置在父节点上
3、当该节点的左孩子或右孩子处于1状态,则返回2;
代码如下
class Solution {
int count = 0;
public int minCameraCover(TreeNode root) {
if(dfs(root)==0){//若头结点的左右子节点都属于有覆盖的情况,那么头结点需要放置一个摄像头
count++;
}
return count;
}
public int dfs(TreeNode node){
//遇到空节点当做有覆盖的情况。理想情况是叶子结点的父节点放摄像头可以使摄像头数量最少。
//如果将空节点当做有摄像头,那么摄像头的数量会非常多;如果将空节点当做无覆盖,那么叶子结点就都需要放摄像头,摄像头数量也会很多。
if(node==null){
return 2;
}
//后序遍历
int left = dfs(node.left);
int right = dfs(node.right);
//当左右子节点均为有覆盖的情况,当前节点返回无覆盖,这样就能让当前节点的父节点放摄像头,而不是在当前节点放摄像头,进而节省摄像头数量
if(left==2&&right==2){
return 0;
}
//当左右子节点至少一个为无覆盖情况,那么当前节点必须放摄像头
if(left==0||right==0){
count++;
return 1;
}
//通过前面两个if的判断,说明当前节点的左右子节点都不是无覆盖情况,也不都是有覆盖情况,说明左右子节点的情况为 两个1 或者 一个1、一个2,此时当前节点返回有覆盖
if(left==1||right==1){
return 2;
}
// 这个 return -1 逻辑不会走到这里。
return -1;
}
}
