普通的数据结构,如果我们想要寻找所存元素中的最大值或者最小值,需要挨个查找。而本章所学的优先队列和堆会按照优先级给元素排序,帮助我们以最快的速度O(1)获取优先级最高的元素。
优先队列
优先队列把优先级最高的元素设为链表的头节点,这样我们获取或删除优先级最高的元素只需要O(1)的时间复杂度,这么设计的代价就是牺牲插入的效率,每次插入一个新的元素时,我们都需要迭代链表,并找到合适的地方插入,这个时间复杂度往往是O(n)。
以下是优先队列支持的操作:
- push:插入一个新的元素
- pop:将优先级最高的元素弹出(删除)
- peek:查看优先级最高的值
使用java实现优先队列
优先队列的定义和链表很相似,首先我们需要定义节点和PriorityQueue:
public class PriorityQueue {
class Node {
int value;
// priority 越大,优先级越高
int priority;
Node next;
public Node(int value, int priority) {
this.value = value;
this.priority = priority;
}
}
// 头结点
Node header = null;
}
其中Node就是队列中的节点,包含value数组和优先级priority,如果希望数值大的节点优先级高,那么可以将priority的数值设为和value一样。反之,我们可以将priority设为数值的相反数,那么在此队列中,一个数值越小,优先级就越高。在PriorityQueue中,我们只需要记录一个头节点head即可。
push方法定义
public void push(int value, int priority) {
// 队列为空,将当前节点设置为头结点
if (header == null) {
header = new Node(value, priority);
return;
}
// 队列不为空,需要找到一个正确的位置将节点插入
Node node = new Node(value, priority);
// 将元素插入到头结点
if (header.priority < priority) {
node.next = header;
header = node;
return;
}
Node current = header;
while (current.next != null && current.next.priority > priority) {
current = current.next;
}
node.next = current.next;
current.next = node;
}
在Push中,我们需要检查是否头节点为空,如果是,就将新的节点设置为头节点。否则我们迭代循环头节点,将新的节点插入一个特定位置,插入后之前节点的优先级都比新节点高,之后节点的优先级都比新节点小。
peek和pop方法定义
/**
* 弹出头结点
*
* @return
*/
public Node pop() {
if (header == null) {
return null;
}
Node tmp = header;
header = header.next;
return tmp;
}
/**
* 返回头结点
*
* @return
*/
public Node peek() {
return header;
}
peek只需要返回头节点即可。pop只需要弹出head的值,并让head指向自己的下一个节点即可。
isEmpty方法定义
isEmpty只需要查看head是否为空:
/**
* 判断队列是否为空
*
* @return
*/
public boolean isEmpty() {
return header == null;
}
方法复杂度分析
- push: O(n)
- pop: O(1)
- peek: O(1)
堆(Heap)
堆(Heap)是一种可以迅速找到一堆数中的最大或者最小值的数据结构,二叉堆(binary heap)是堆的一种实现,计算机中一般使用数组存储二叉堆。
堆是一颗完全二叉树,堆中的节点满足以下的条件:一个节点的父节点优先级比自己高,而自己的子节点优先级比自己底。优先级可以根据数值的大小来决定。最常见的堆有以下两种类型:
-
最大堆(Max Heap):根节点数值最大,所有父节点的数值比各自的子节点数值大或等于子节点,很多地方也叫大顶堆。

-
最小堆(Min Heap):根节点数值最小, 父节点数值比其子节点数值小或等于子节点,很多地方也叫小顶堆。
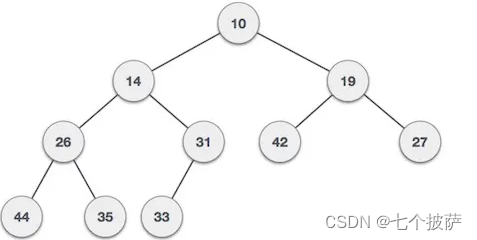
最大堆(Max Heap)
最大堆的基本操作:
- add: 将新元素插入堆
- poll: 将根节点(数值最大的元素)删除
- peek: 获取根节点的数值
在任何的时间点,最大堆都应该保持其特性:父节点的数值比所有子节点大。在插入新元素的时候,我们要遵循以下步骤:
- 在堆的最后新建一个节点,将数值赋予新节点。
- 将其节点和父节点比较。
- 如果新节点的数值比父节点大,调换父子节点的位置。
- 重复步骤2和3直到最大堆的特性被满足。
以下是删除根节点的步骤:
- 移除根节点
- 将最后一个节点移到根节点处
- 将子节点和父节点比较
- 如果父节点的数值比子节点小,替换父子节点
- 重复步骤3和4直到最大堆的特性被满足。
使用数组实现最大堆
因为堆是一颗完全二叉树,因此我们可以直接使用数组而不是链表来实现堆。
最大堆的基本定义
public class MaxHeap {
// 容量,当前最大堆可承载的节点数。当容量不足时需要扩容
private int capacity;
// 当前最大堆的节点数
private int size = 0;
// 用于存储节点
private int[] array;
public MaxHeap(int capacity) {
this.capacity = capacity;
this.array = new int[capacity];
}
}
以下是一些有用的helper method:
// 最大堆中,左子节点位置为 父节点下标 * 2 + 1
public int getLeftChildIndex(int index) {
return index * 2 + 1;
}
// 最大堆中,右子节点位置为 父节点下标 * 2 + 2
public int getRightChildIndex(int index) {
return index * 2 + 2;
}
// 父节点下标为 (子节点下标 - 1)/2
public int getParentIndex(int index) {
return (index - 1) / 2;
}
// 判断是否存在左子节点,只需要判断左子节点的下标是否小于当前数组节点数
public boolean hasLeftChild(int index) {
return getLeftChildIndex(index) < size;
}
public boolean hasRightChild(int index) {
return getRightChildIndex(index) < size;
}
public boolean hasParent(int index) {
return getParentIndex(index) >= 0;
}
add方法
add方法的作用是新增节点到堆中。在add时,我们首先需要判断数组是否已经存储满了,如果存储满了,需要先对数组进行扩容。接着在堆的最后放入新节点,然后使用heapifyUp将节点上移。heapifyUp的作用是不断将子节点和父节点比较,如果子节点比父节点优先级大,就交换父子节点的位置。
/**
* 核心方法 add:新增节点到最大堆中;步骤:
* 1.在堆的最后新建一个节点,将数值赋值给新节点;
* 2.将子节点和父节点比较;
* 3.如果父节点数值比子节点小,交换父子节点位置;
* 4.重复步骤2和步骤3,直到满足最大堆的特性。
*
* @param item
*/
public void add(int item) {
if (capacity == size) {
capacity = 2 * size;
array = Arrays.copyOf(array, capacity);
}
array[size] = item;
size++;
heapifyUp();
}
private void heapifyUp() {
int index = size - 1;
int parentIndex = getParentIndex(index);
// 将子节点和父节点比较
while (hasParent(index) && array[parentIndex] < array[index]) {
// 交换父子节点位置
int tmp = array[parentIndex];
array[parentIndex] = array[index];
array[index] = tmp;
index = parentIndex;
parentIndex = getParentIndex(index);
}
}
poll方法
poll方法的作用是移除堆的根节点,也就是数组下标为0的节点。移除根节点后,需要将堆的最后一个节点替代上去,然后再使用heapifyDown将节点下移以满足最大堆的特性。heapifyDown方法的作用是将父节点不断和其子节点做比较,如果父节点的优先级比子节点优先级小,就交换父子节点的位置。
/**
* 核心方法 poll:移除根节点;步骤:
* 1.将堆的最后一个节点放到根节点;
* 2.将父节点和子节点比较;
* 3.如果父节点比子节点小,交换父子节点位置;
* 4.重复步骤2和步骤3,直到满足最大堆的特性。
*/
public void poll() {
if (size == 0) {
return;
}
array[0] = array[size - 1];
size--;
heapifyDown();
}
private void heapifyDown() {
int index = 0;
while (hasLeftChild(index)) {
int largerChildIndex;
if (hasRightChild(index) && array[getRightChildIndex(index)] > array[getLeftChildIndex(index)]) {
largerChildIndex = getRightChildIndex(index);
} else {
largerChildIndex = getLeftChildIndex(index);
}
if (array[largerChildIndex] < array[index]) {
break;
}
int tmp = array[largerChildIndex];
array[largerChildIndex] = array[index];
array[index] = tmp;
index = largerChildIndex;
}
}
peek方法
/**
* 核心方法peek:返回堆的根节点。先不考虑size为0的情况
*
* @return
*/
public int peek() {
return array[0];
}
方法复杂度分析
- add: O(logN)
- poll: O(logN)
- peek: O(1)
附一个可以测试最大堆的一个网站:https://visualgo.net/zh/heap
堆排序
一个讲堆排序比较好的B站视频:https://www.bilibili.com/video/BV1B64y1975b?spm_id_from=333.337.search-card.all.click
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆排序可以说是一种利用堆的概念来排序的选择排序。一般升序排序时会采用大顶堆的方式,降序时采用小顶堆。
堆排序的平均时间复杂度为O(n log(n)),空间复杂度为O(1)。堆排序是不稳定的排序算法。
算法步骤
- 构造初始堆。将给定的无序数列构造成一个大顶堆(如果是降序则构造小顶堆);
- 将堆顶元素(最大值)与末尾元素交换位置,使末尾元素最大,堆长度减一。然后继续调整,使其再次满足大顶堆的特性;
- 重复步骤2,等到堆中元素只剩下一个后,说明排序完成。
java实现
在讲堆排序的java实现之前先插播一个知识点:
数组实现的完全二叉树中,假设数组长度为n,最后一个非叶子节点的下标为
n/2-1。
推导过程如下:
- 在完全二叉树中,对于下标为
index的节点,其左孩子下标为2*index+1,右孩子的下标为2*index+2。由此可以推导出下标为index的节点的父节点下标为(index-1)/2; - 在节点数为 n 满二叉树中,最后一个叶子节点的下标为 n-1,带入上一个公式得出最后一个非叶子节点坐标为
n/2-1。
public int[] heapSort(int[] sourceArray) {
int[] array = Arrays.copyOf(sourceArray, sourceArray.length);
// 构造大顶堆
buildMaxHeap(array);
// 将堆顶元素与末尾元素交换位置后继续调整使其满足大顶堆特性,直到堆中只剩下一个元素
for (int i = array.length - 1; i > 0; i--) {
swap(array, 0, i);
heapify(array, 0, i);
}
return array;
}
private void buildMaxHeap(int[] array) {
// 构造大顶堆。从最后一个非叶子节点开始不断heapify
// 先局部调整为大顶堆,然后再逐渐向上调整,使整个堆满足大顶堆特性
for (int i = array.length / 2 - 1; i >= 0; i--) {
heapify(array, i, array.length);
}
}
private void heapify(int[] array, int index, int len) {
// 下标为index的节点的左孩子下标
int left = 2 * index + 1;
// 下标为index的节点的右孩子下标
int right = 2 * index + 2;
int larger = index;
if (left < len && array[left] > array[larger]) {
larger = left;
}
if (right < len && array[right] > array[larger]) {
larger = right;
}
// 父节点比子节点小,交换父子节点位置
if (larger != index) {
swap(array, index, larger);
// 父子节点位置交换后,一边子树发生了变化,需要重新heapify使其继续满足最大堆特性
heapify(array, larger, len);
}
}
private void swap(int[] array, int index1, int index2) {
int tmp = array[index1];
array[index1] = array[index2];
array[index2] = tmp;
}
附录
堆排序完整代码+测试
public class 堆排序 {
public int[] heapSort(int[] sourceArray) {
int[] array = Arrays.copyOf(sourceArray, sourceArray.length);
// 构造大顶堆
buildMaxHeap(array);
// 将堆顶元素与末尾元素交换位置后继续调整使其满足大顶堆特性,直到堆中只剩下一个元素
for (int i = array.length - 1; i > 0; i--) {
swap(array, 0, i);
heapify(array, 0, i);
}
return array;
}
private void buildMaxHeap(int[] array) {
// 构造大顶堆。从最后一个非叶子节点开始不断heapify
// 先局部调整为大顶堆,然后再逐渐向上调整,使整个堆满足大顶堆特性
for (int i = array.length / 2 - 1; i >= 0; i--) {
heapify(array, i, array.length);
}
}
private void heapify(int[] array, int index, int len) {
// 下标为index的节点的左孩子下标
int left = 2 * index + 1;
// 下标为index的节点的右孩子下标
int right = 2 * index + 2;
int larger = index;
if (left < len && array[left] > array[larger]) {
larger = left;
}
if (right < len && array[right] > array[larger]) {
larger = right;
}
// 父节点比子节点小,交换父子节点位置
if (larger != index) {
swap(array, index, larger);
// 父子节点位置交换后,一边子树发生了变化,需要重新heapify使其继续满足最大堆特性
heapify(array, larger, len);
}
}
private void swap(int[] array, int index1, int index2) {
int tmp = array[index1];
array[index1] = array[index2];
array[index2] = tmp;
}
public static void main(String[] args){
int[] array = new int[]{2,7,26,25,19,17,1,90,3,36};
array = new 堆排序().heapSort(array);
StringBuilder builder = new StringBuilder();
builder.append("[").append(array[0]);
for (int i = 1; i < array.length; i++) {
builder.append(",").append(array[i]);
}
builder.append("]");
System.out.println(builder.toString());
}
}
